二次関数では平行移動という用語が登場します。平行移動は大学入試や共通テストでも頻出の用語なので、必ず理解しておく必要があります。
そこで今回は、早稲田大学教育学部数学科を卒業した筆者が二次関数の平行移動とは何かについて解説した後、平行移動の公式や平行移動の証明などについても解説します。
最後には平行移動に関する練習問題も用意しているので、ぜひ最後までご覧ください。
二次関数の平行移動とは?公式も
まずは二次関数の平行移動は何かについて解説します。
二次関数の平行移動とは二次関数のグラフの形や向きは変えずに、そのグラフの位置だけ移動させることです。
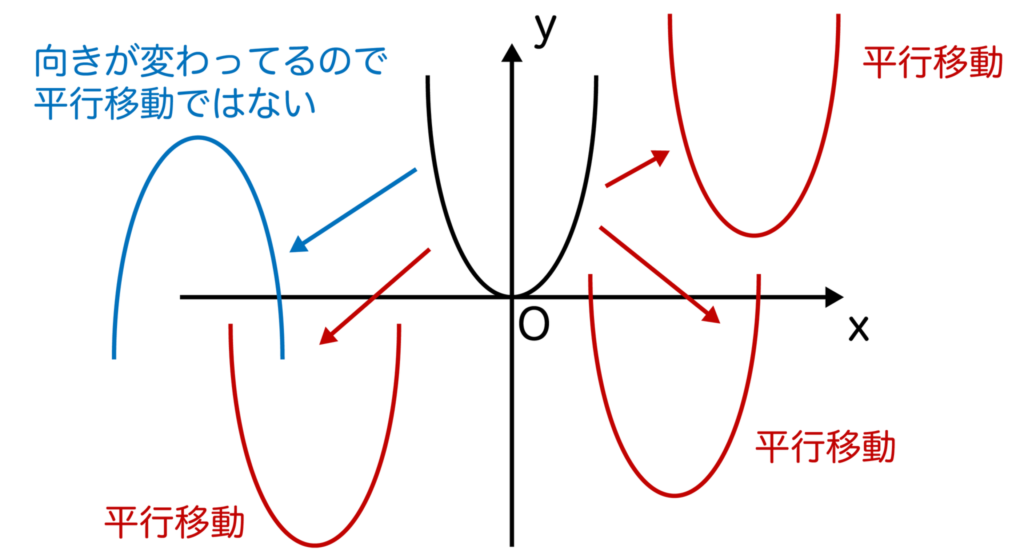
そして、二次関数y=ax2をx軸方向にp、y軸方向にqだけ平行移動させたグラフはy=a(x-p)2+qとなります。
二次関数y=ax2をx軸方向にp、y軸方向にqだけ平行移動させるということは頂点が(0、0)から(p、q)に移行することを意味していますね。
二次関数の頂点について解説した記事をご覧いただくとわかりますが、頂点が(p、q)の二次関数のグラフはy=a(x-p)2+qと表すことができましたね。
以上は二次関数の頂点・平行移動に関する公式として覚えてください。
では、1つ例題を解いてみましょう。
【例題】
二次関数y=2x2をx軸方向に4、y軸方向に-5だけ平行移動させたグラフの式を求めよ。
【解答&解説】
以上の平行移動に関する公式より、y=2(x-4)2-5・・・(答)となります。
※展開してy=2x2-16x+27としても問題ありません。展開のやり方がわからない人は多項式の計算方法について解説した記事をご覧ください。
では、y=ax2+bx+cをx軸方向にp、y軸方向にqだけ平行移動したグラフの式はどうなるでしょうか?
結論から述べますと、y=a(x-p)2+(x-p)b+c+qとなります。
これも公式として必ず覚えておきましょう。
xを(x-p)に置き換えて、最後にqを足しているだけです。
※先ほど解説したy=ax2のグラフをx軸方向にp、y軸方向にqだけ平行移動したグラフの式はy=a(x-p)2+qでしたが、これもxを(x-p)に置き換えて最後にqを足しているだけです。
では、1つ例題を解いてみましょう。
【例題】
二次関数y=2x2-4x+1をx軸方向に2、y軸方向に-3だけ平行移動させたグラフの式を求めよ。
【解答&解説】
以上で解説した公式の通り、xを(x-2)に置き換えて、最後に-3を足しましょう。
y=2(x-2)2-4(x-2)+1-3=2x2-12x+14・・・(答)となります。
以上が二次関数の平行移動の解説となります。そこまで難しい内容ではなかったと思います。
平行移動は大学入試や共通テストでもかなり頻出なので必ず覚えておきましょう。
二次関数の平行移動は頂点に注目する方法でも解ける
先ほどは二次関数y=2x2-x+1をx軸方向に2、y軸方向に-3だけ平行移動させたグラフの式を公式を使って求めましたが、頂点に注目して解く方法もあるので念のため解説しておきます。
まずはy=2x2-x+1の頂点を求めます。
y=2x2-4x+1を平方完成するとy=2(x-1)2-1となりますね。
※平方完成のやり方がわからない人は二次関数の平方完成の公式・やり方について解説した記事をご覧ください。
よって、y=2x2-4x+1の頂点は(1、-1)となります。この頂点をx軸方向に2、y軸方向に-3だけ平行移動させると(1+2、-1-3)=(3、-4)となりますね。
よって、二次関数y=2x2-x+1をx軸方向に2、y軸方向に-3だけ平行移動させたグラフの式は、
y=2(x-3)2-4と求めることができます。
※y=2(x-3)2-4=2(x2-6x+9)-4なので、しっかり2x2-12x+14となっています。
頂点がすぐに求めれそうなときは平行移動の公式を使うよりも楽に解ける場合があるので、どちらもできるようにしておきましょう。
二次関数の平行移動の証明
ここからは、以上でご紹介した二次関数の平行移動の公式がなぜ成り立つのかの証明を行います。
※二次関数のグラフFをx軸方向にp、y軸方向にqだけ平行移動して得られる二次関数のグラフをGとします。
(証明)
Fをy=ax2とします。
G上に任意の点P(x、y)を取り、点Pをx軸方向にp、y軸方向にqだけ平行移動した点をQ(X、Y)とします。
すると、x=X+p、y=Y+qよりX=x-p、Y=y-qとなりますね。
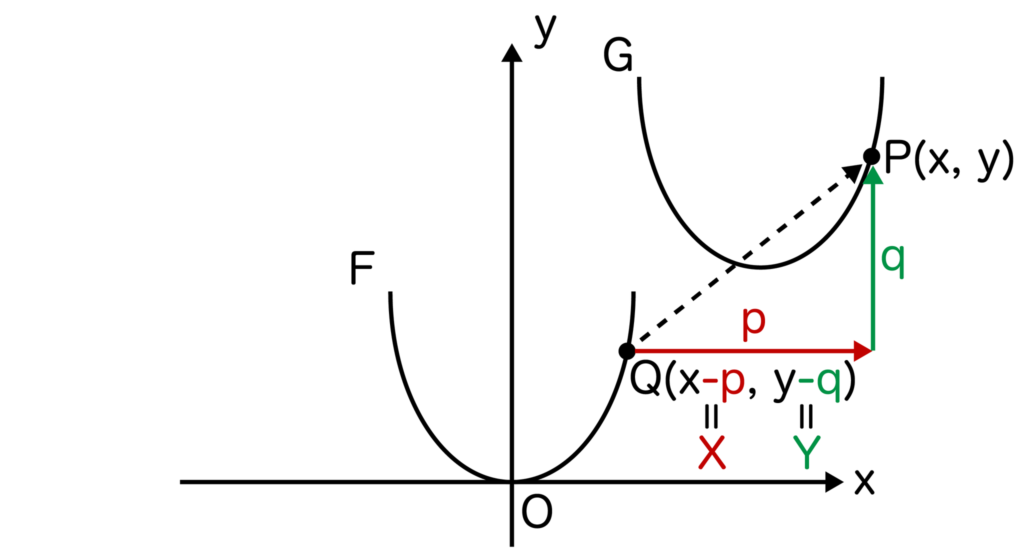
点QはF上にあるのでY=aX2が成り立ちます。
これにX=x-p、Y=y-qを代入すると、Gの方程式は
y-q=a(x-p)2となることがわかり、証明終となります。
少し全貌を捉えるのが難しい証明ですが、最も重要なのは平行移動の公式を暗記することです。
証明の理解は必須ではないので数学が苦手な人はそこまで気にしなくても大丈夫です。
二次関数における逆の平行移動
逆の平行移動とは以下のような問題のことです。
【例題】
ある二次関数をx軸方向に-1、y軸方向に2だけ平行移動させた結果、y=2x2+3x-4になった。もとの二次関数の式を求めよ。
【解答&解説】
ある二次関数をx軸方向に-1、y軸方向に2だけ平行移動させた結果、y=2x2+3x-4になったということは、もとの二次関数はy=2x2+3x-4をx軸方向に1、y軸方向に-2だけ平行移動させれば求まりますね。
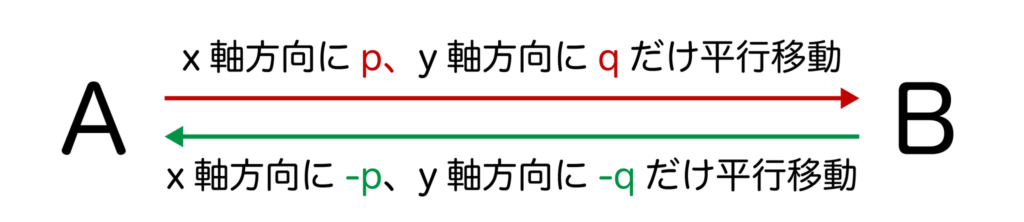
よって、y=2(x-1)2+3(x-1)-4-2=2x2-x-7・・・(答)となります。
逆の平行移動も大学入試や共通テストで頻出なので、必ずできるようにしておきましょう。
二次関数の平行移動に関する練習問題
最後に、二次関数の平行移動に関する練習問題をご用意しました。
どれも基本的な問題なので、すべて問題なく解けるようにしておきましょう。
【練習問題】
(1)二次関数y=-4x2+5をx軸方向に-1、y軸方向に8だけ平行移動させた二次関数の式を求めよ。
(2)二次関数y=x2+6x-1をx軸方向に4、y軸方向に-3だけ平行移動させた二次関数の式を頂点の座標を利用して求めよ。
(3)ある二次関数をx軸方向に5、y軸方向に-1だけ平行移動させた結果、y=-x2-10になった。もとの二次関数の式を求めよ。
【解答&解説】
(1)xを(x+1)に置き換えて、最後に8を足すだけですね。
y=-4(x+1)2+5+8より、y=-4x2-8x+9・・・(答)となります。
(2)まずはy=x2+6x-1を平方完成して頂点を求めましょう。
x2+6x-1=(x+3)2-10より、頂点の座標は(-3、-10)です。
この頂点をx軸方向に4、y軸方向に-3だけ移動させた点は(-3+4、-10-3)=(1、-13)となりますね。
よって、求める二次関数はy=(x-1)2-13・・・(答)となります。
(3)もとの二次関数はy=-x2-10をx軸方向に-5、y軸方向に1だけ平行移動させれば良いので、xを(x+5)に置き換えて、最後に1を足しましょう。
したがって、y=-(x+5)2-10+1=-x2-10x-34・・・(答)となります。
今回は二次関数の平行移動とは何かについて解説した後、平行移動の公式や逆の平行移動についても解説しました。
平行移動は二次関数の分野において非常に重要な事柄です。必ず公式を覚えてできるようにしておいてください。
※平行移動と一緒に対称移動も大学入試や共通テストで頻出です。二次関数の対称移動について解説した記事もぜひ合わせてご覧ください。


