高校数学の数学1における「データの分析」で登場する最重要用語の1つが分散です。
分散は標準偏差とともに使われることが多いですが、分散をしっかりと理解しておかないと標準偏差も理解できません。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が分散とは何かについて解説した後、分散の求め方や公式、分散を使って分析できることなどについて解説していきます。
また、標準偏差との関係についても簡単に解説しているので、ぜひ最後までお読みください。
分散とは?分析できること
中央値の周りのデータの散らばり具合を知るためには四分位偏差を使うのでしたね。
※詳しくは四分位数とは何かについて解説した記事をご覧ください。
それに対して、平均値の周りのデータの散らばり具合を数値化したものを分散といいます。
例えば、以下2つのケースを考えてみましょう。
- あるテストを受験した結果、Aさんは100点、Bさんは0点だった
- Aさん、Bさんと同じテストをCさん、Dさんも受験した結果、Cさんは50点、Dさんも50点だった
この場合、
- 1の平均値=(100+0)/2=50[点]
- 2の平均値=(50+50)/2=50[点]
となり、ともに平均値=50[点]であることがわかります。
しかし、1の2人(Aさん・Bさん)と2の2人(Cさん・Dさん)の状況が同じであるとは言えなさそうですね。
1の場合は2人の点数が平均値から散らばっていますが、2の場合は2人の点数が平均値の周りに集まっています。
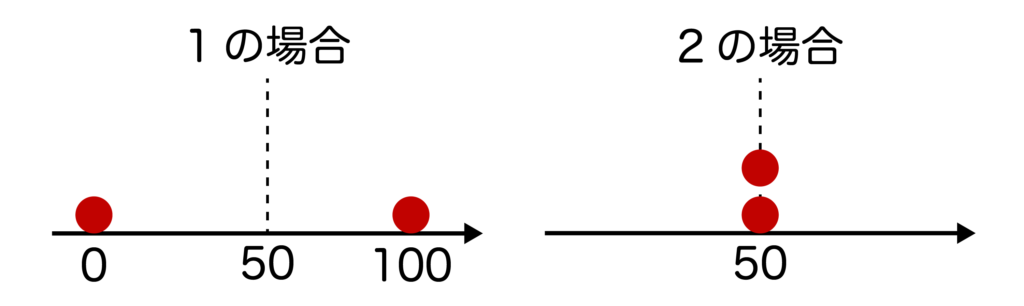
以上が平均値周りのデータの散らばり具合とは何かを示した例となります。
分散を求めることで平均値の周りのデータの散らばり具合を数値化・分析できるということをまずは理解しておきましょう。
また、
- 平均値からデータが散らばっていることを「分散が大きい」
- 平均値の周りにデータが集中していることを「分散が小さい」
というので、こちらも必ず覚えておきましょう。
上記の例だと、1の場合は分散が大きい、2の場合は分散が小さいとなります。
分散の求め方・公式
ここからは分散の具体的な求め方・公式について例題で解説していきます。
【例題】
生徒が8人いるクラスで数学と英語のテスト(ともに10点満点)を実施した。生徒8人の点数は以下である。
このとき、数学と英語の点数の分散をそれぞれ求めよ。
| 数学 | 8 | 7 | 7 | 8 | 6 | 6 | 7 | 7 |
| 英語 | 2 | 4 | 7 | 5 | 7 | 4 | 3 | 8 |
【解答&解説】
分散は以下の手順で求めることができます。
- データの平均値を求める
- 各データの偏差(=各データの値-平均値)を求める
- 各データの偏差の平方を求める
- 偏差平方の平均を求める
では、順番に解説していきます。
データの平均値を求める
まずはデータの平均値を求めます。
- 数学の平均値=(8+7+7+8+6+6+7+7)/8=56/8=7[点]
- 英語の平均値=(2+4+7+5+7+4+3+8)/8=40/8=5[点]
となりますね。
各データの偏差(=各データの値-平均値)を求める
続いては各データの値-平均値を求めていきます。
数学における各データの値-平均値の一覧は以下のようになりますね。
| 数学の点数 | 点数(=各データの値)-平均値 |
|---|---|
| 8 | 8-7=1 |
| 7 | 7-7=0 |
| 7 | 7-7=0 |
| 8 | 8-7=1 |
| 6 | 6-7=-1 |
| 6 | 6-7=-1 |
| 7 | 7-7=0 |
| 7 | 7-7=0 |
一方で、英語における各データの値-平均値の一覧は以下のようになりますね。
| 英語の点数 | 点数(=各データの値)-平均値 |
|---|---|
| 2 | 2-5=-3 |
| 4 | 4-5=-1 |
| 7 | 7-5=2 |
| 5 | 5-5=0 |
| 7 | 7-5=2 |
| 4 | 4-5=-1 |
| 3 | 3-5=-2 |
| 8 | 8-5=3 |
ちなみにですが、以上で求めた「各データの値-平均値」のことを偏差といいます。必ず覚えておきましょう。
ここまでは全然難しい話ではないかと思います。
各データの偏差の平方を求める
次は先ほど求めた偏差の平方を求めます。平方とは2乗のことです。
※偏差の平方のことをそのままですが偏差平方といいます。
数学における各データの偏差の平方一覧は以下のようになりますね。
| 数学の点数 | 点数(=各データの値)-平均値 | 偏差(=2列目)の平方 |
|---|---|---|
| 8 | 8-7=1 | 1 |
| 7 | 7-7=0 | 0 |
| 7 | 7-7=0 | 0 |
| 8 | 8-7=1 | 1 |
| 6 | 6-7=-1 | 1 |
| 6 | 6-7=-1 | 1 |
| 7 | 7-7=0 | 0 |
| 7 | 7-7=0 | 0 |
一方で、英語における各データの偏差の平方一覧は以下のようになりますね。
| 英語の点数 | 点数(=各データの値)-平均値 | 偏差(=2列目)の平方 |
|---|---|---|
| 2 | 2-5=-3 | 9 |
| 4 | 4-5=-1 | 1 |
| 7 | 7-5=2 | 4 |
| 5 | 5-5=0 | 0 |
| 7 | 7-5=2 | 4 |
| 4 | 4-5=-1 | 1 |
| 3 | 3-5=-2 | 4 |
| 8 | 8-5=3 | 9 |
ここまできたら分散を求めるまであと一歩です。
偏差平方の平均を求める
いよいよ最後のステップとなります。先ほど求めた偏差平方の平均を求めることで分散が計算されます。
つまり、数学の分散=(1+0+0+1+1+1+0+0)/8=4/8=0.5となります。
英語の分散=(9+1+4+0+4+1+4+9)/8=32/8=4となります。
以上で分散を求めることができました。分散の求め方は問題をたくさん解いていくうちに自然と覚えるようになるので、たくさんの問題を解くことを心がけてください。
ちなみに、数学の分散=0.5、英語の分散=4より、数学の分散<英語の分散ですね。
これはつまり、数学のテストの方が英語のテストよりも平均値の周りにデータが集中しているということになります(=分散が小さい)
分散と標準偏差について
先ほど分散の求め方について解説しましたが、分散を求めるために偏差を平方(=2乗)しましたね。
偏差=各データの値-平均値なので、単位は[点]ですが、分散では、偏差を平方することによって単位が[点2]になってしまいます。
[点]という単位は理解できますが、[点2]という単位は正直何を意味するのかわかりませんね。
分散では単位がおかしなことになってしまうというデメリットがあるので、単位をもとのデータと揃えたいと思うわけです。
そこで、分散の正の平方根の値を考えるのです。
※平方根がわからない人は平方根とは何かについて解説した記事をご覧ください。
この値(=分散の正の平方根)のことを標準偏差といいます。
上記の例題だと、
- 数学の分散=0.5(=1/2)
- 英語の分散=4
だったので、
- 数学の標準偏差=1/√2
- 英語の標準偏差=2
となります。
標準偏差も分散と同じく、値が大きければデータが散らばっていることを意味し、値が小さければ平均値の周りにデータが集中していることを意味します。
標準偏差について詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
分散と平均値の関係について
先ほどまではデータの平均値を求める→各データの偏差を求めるという手順を踏んで分散を求めていきましたが、分散の求め方はもう1つあります。
分散=各データの2乗の平均値-平均値の2乗
でも求めることができます。これは分散の公式として覚えておきましょう。
※証明については大学入試・共通テストにおいてそこまで重要ではないと判断したので、割愛させていただきます。
以上の分散の公式を使って例題を1つ解いてみましょう。
【例題】
ある学校のAクラスの人数は50人で、内訳は男子が30人、女子が20人である。このAクラスで生徒50人の身長を測定したところ、以下の結果が得られた。
| 性別 | 平均身長 | 分散 |
|---|---|---|
| 男子 | 170cm | 36 |
| 女子 | 160cm | 16 |
(1)Aクラスの生徒全員の平均身長は何cmか求めなさい。
(2)Aクラスの生徒全員の分散と標準偏差を求めなさい。
【解答&解説】
(1)男子30人の平均身長=170cmなので、男子30人の合計身長÷30=170となることがわかります。
したがって、男子30人の合計身長=170×30=5100[cm]です。
同様に考えて、女子20人の合計身長=160×20=3200[cm]となります。
つまり、生徒全員の合計身長=5100+3200=8300[cm]です。生徒は全部で50人なので、
生徒全員の平均身長=8300÷50=166[cm]・・・(答)となります。
(2)先ほどご紹介した分散の公式「分散=各データの2乗の平均値-平均値の2乗」を使いましょう。
男子の身長の分散は36なので、36=男子の各データの2乗の平均値-1702となります。
つまり、男子の各データの2乗の平均値=36+1702=28936です。
ここで、男子の各データの2乗の平均値=男子の各データの2乗の合計/30より、
男子の各データの2乗の合計=28936×30=868080・・・①となります。
同様に考えて、16=女子の各データの2乗の平均値-1602より、
女子の各データの2乗の平均値=16+1602=25616となるので、
女子の各データの2乗の合計=25616×20=512320・・・②となります。
(1)より生徒全員の平均身長=166cmなので、
生徒全員の分散=(①+②)/50-1662=1380400/50-1662=52・・・(答)となります。
分散と外れ値の関係について
度数分布表の平均値の求め方について解説した記事でも解説しましたが、平均値は外れ値に影響を受けやすい代表値です。
分散は平均値を使って値を計算しているので、分散も外れ値に影響を受けやすいという弱点があります。
また、分散は複数の種類のデータが混ざっている可能性のあるデータ(=ヒストグラムにしたとき、山が2つ以上存在する場合)では信頼性が低下してしまうという弱点もあるのでご注意ください。
データの分析で重要なのは、目的に対してどんな手法を取ればその目的を達成することができるか?を考えることです。
統計や科学などの世界では、目的を達成する上では分散や平均値を求めることが必ずしも正しいとは限らないということを理解しておきましょう。
いかがでしたか?今回は分散とは何か・分散で分析できることについて解説した後、分散の求め方や公式について解説しました。
分散は標準偏差と並んでデータの分析において最重要用語の1つなので、必ず計算できるようにしておきましょう!


