高校数学の数学1における「データの分析」では四分位数という用語が登場します。
四分位数の読み方は「しぶんいすう」なので覚えておきましょう。
四分位数はデータの分析や統計において非常に重要な用語の1つです。
本記事では早稲田大学教育学部数学科を卒業した筆者が四分位数とは何かや四分位数の求め方はもちろんのこと、四分位数と第1四分位数や箱ひげ図との関係についても解説していきます。
数学やデータの分析が苦手な高校生向けにわかりやすく解説しているので、ぜひ最後までご覧ください。
四分位数とは?わかりやすく解説
早速、四分位数とは何かについて例を使いながら解説していきます。
ある学校のクラスでテストが行われ、そのテストを受けた生徒の点数を小さい順に並べたとき、以下のようになったとしましょう(単位:点)
40、43、56、57、63、66、70、79、82、84、93
そして、生徒Aはこのクラスで上から4番目の点数だったとします。
上から4番目というのは素晴らしい成績ですが、では、この生徒Aはこの学校の中でトップ集団に属していると言えるかを考えてみましょう。
クラスの中で順位が真ん中よりも上か下かを調べるときは平均値よりも中央値を見た方が良いのでした。
※詳しくは度数分布表の平均値の求め方について解説した記事をご覧ください。
しかし、中央値から判断できるのは真ん中よりも上か下かどうかなので、トップ集団に自分が属しているかどうかまではわからないという弱点があります。
そのようなときは、データ全体を四等分してみるのです。
今回の場合、中央値=66ですね。
そして、中央値の66よりも左側の数字は
40、43、56、57、63
であり、この部分にのみ注目した場合の中央値=56ですね。
また、中央値の66よりも右側の数字は
70、79、82、84、93
であり、この部分にのみ注目した場合の中央値=82ですね。
データ全体は以上3つの数字(66、56、82)によって四等分できると考えます。
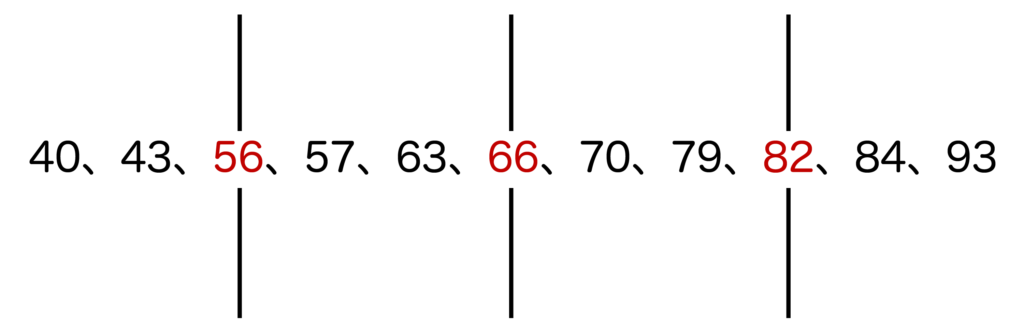
以上3つの数字(56、66、82)をそれぞれ第1四分位数、第2四分位数、第3四分位数といい、合わせて四分位数といいます。
第2四分位数=データ全体の中央値のことです。
正確に言うときっちり四等分できているわけではないのですが、四分位数の学習では各グループにデータの約25%が含まれていればOKとみなします。
ちなみに、四分位数は英語で「quartile」といい、第1四分位数、第2四分位数、第3四分位数はそれぞれ記号でQ1、Q2、Q3と表現されることが多いので覚えておきましょう。
話を戻して、生徒Aはこのクラスで上から4番目の点数であり、生徒Aはこの学校の中でトップ集団に属していると言えるかを考えてみましょう。
データ全体を四等分したことにより、生徒Aの点数=79点(上から4番目)は第2四分位数(=66)と第3四分位数(=82)の間にあることがわかり、上位25%のグループには入っていないのでトップ集団に属しているとは言えなさそうです。
四分位数の求め方(データの個数=偶数個の場合)
ここからは四分位数の求め方についてより詳しく解説していきます。
四分位数の求め方はデータの個数が偶数個か奇数個かによって変わるので注意が必要です。
まずはデータの個数が偶数個のケースから解説していきます。
以下のデータ(あるクラスのテストの点数を小さい順にまとめたもの)の四分位数を求めてみます。
| テストの点数 | 度数 |
|---|---|
| 55、60、63、65、72、76、80、84、86、96 | 10 |
まずは第2四分位数から求めましょう。
第2四分位数=全データの中央値のことでした。
したがって、第2四分位数=(72+76)/2=74となります。
※中央値が(72+76)/2=74になる理由がわからない人は度数分布表から中央値を求める方法について解説した記事をご覧ください。
第1四分位数は小さい方の半分のデータの中央値である63となります。
第3四分位数は大きい方の半分のデータの中央値である84となります。
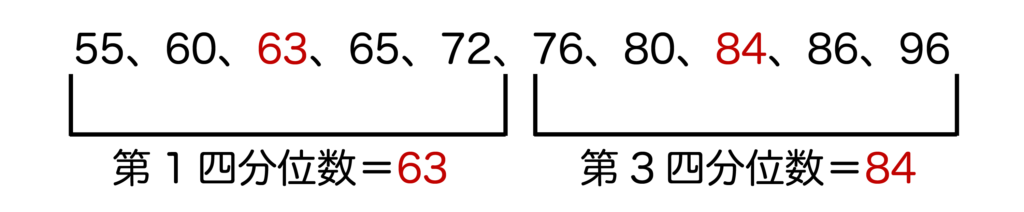
以上がデータの個数=偶数個の場合の四分位数の求め方となります。
四分位数の求め方(データの個数=奇数個の場合)
続いてはデータの個数が奇数個の場合の四分位数の求め方について解説します。
以下のデータ(あるクラスのテストの点数を小さい順にまとめたもの)の四分位数を求めてみましょう。
| テストの点数 | 度数 |
|---|---|
| 30、42、58、80、84、86、88、90、92 | 9 |
まずは第2四分位数から求めましょう。
第2四分位数=データ全体の中央値=84となります。
第1四分位数は中央値(=第2四分位数)を除いた小さい方の半分のデータの中央値で、(42+58)/2=50となります。
第3四分位数は中央値(=第2四分位数)を除いた大きい方の半分のデータの中央値で、(88+90)/2=89となります。
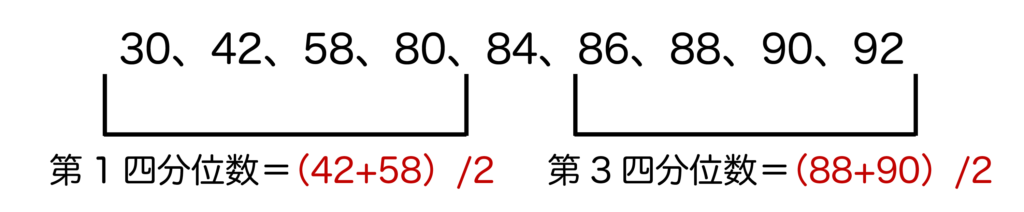
以上がデータの個数=奇数個の場合の四分位数の求め方となります。
四分位数の求め方はデータの個数が偶数個か奇数個かで変わるので、両方ともしっかり解けるようにしておきましょう。
範囲・四分位範囲・四分位偏差とは?
四分位数とは何かがわかったところで、ここからは範囲・四分位範囲・四分位偏差とは何かについて解説します。
以下のデータを例に解説していきます。
| テストの点数 | 度数 |
|---|---|
| 30、45、50、78、84、86、87、88、90、92 | 10 |
範囲
範囲とは、データの最大値から最小値を引いた値のことです。
最大値とはその名の通りデータの中で最も大きい値のことです。最小値はデータの中で最も小さい値のことです。
以上のデータの最大値=92、最小値=30なので、範囲=92-30=62[点]となります。
範囲にはデータの100%が含まれているのが特徴です。
ちなみにですが、
- 最大値
- 最小値
- 第1四分位数
- 第2四分位数
- 第3四分位数
の5つを合わせて5数要約というので覚えておきましょう。
※5数要約について詳しく解説した記事もぜひ合わせてご覧ください。
四分位範囲
四分位範囲とは、第3四分位数から第1四分位数を引いた値のことです。
上記のデータにおいて、
- 第3四分位数=88
- 第1四分位数=50
なので、四分位範囲=88-50=38[点]となります。
四分位範囲にはデータの約50%が含まれているのが特徴です。
四分位偏差
四分位偏差=四分位範囲÷2となります。
上記のデータにおいて、四分位範囲は先ほど求めた通り38点なので、四分位偏差=38÷2=19[点]となります。
四分位範囲や四分位偏差の値が小さいほど、中央値の周りにデータが集まっていることになります。
四分位数と箱ひげ図の書き方
以上では、中央値の周りのデータの散らばり具合を調べるために5数要約や四分位範囲、四分位偏差について解説しました。
しかし、5数要約は実際にデータの傾向をつかもうとしたとき、
- 5数要約を何種類かのデータをもとに計算しても、それらが比較しにくい
- データを整理するときに、度数分布表からヒストグラムを作成することはできるが、複数のヒストグラムだと比較しにくい
と言う弱点があります。このような問題を解消するために箱ひげ図というグラフはあります。
箱ひげ図を活用することで5数要約をわかりやすく表にすることができ、複数のデータの比較がしやすくなります。
箱ひげ図は以下のようなイメージです。
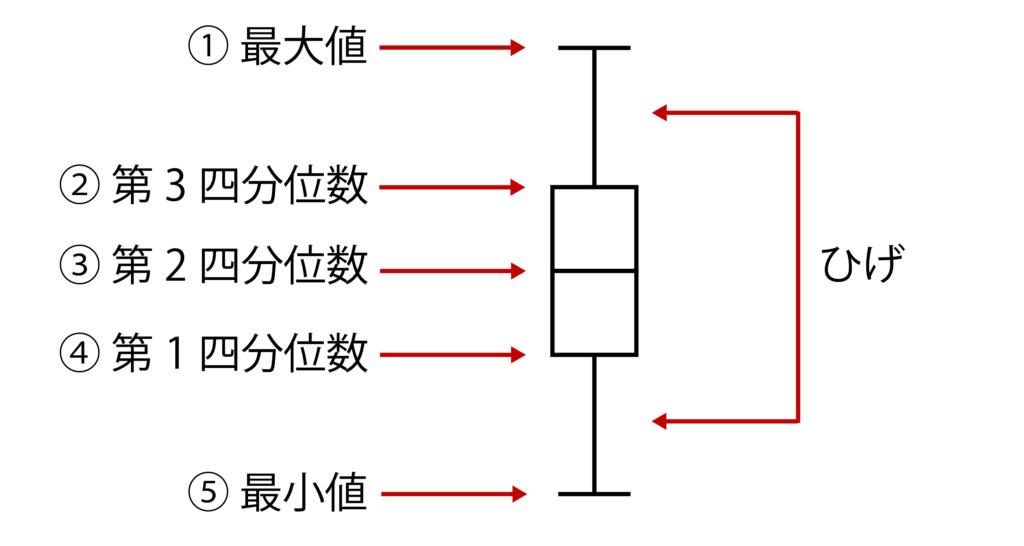
では、以下のデータをもとにして箱ひげ図を書いてみましょう。
| テストの点数 | 度数 |
|---|---|
| 56、68、86、62、72、77、65、94、84、82 | 10 |
データを小さい順に並べると「56、62、65、68、72、77、82、84、86、94」となるので、
- 最大値=94
- 第3四分位数=84
- 第2四分位数=(72+77)/2=74.5
- 第1四分位数=65
- 最小値=56
となりますね。
箱ひげ図の書き方その1
まずは第1四分位数=65と第3四分位数=84をとり、以下のように長方形を作ります。

箱ひげ図の書き方その2
次は第2四分位数=74.5をとり、長方形の中に縦印(以下の図における赤線)を入れます。

箱ひげ図の書き方その3
次は箱の左から最小値(=56)まで線分(ひげ)を引きます。
そして、箱の左側(第1四分位数の部分=65)から最小値(=56)まで線分を引きます。

箱ひげ図の書き方その4
次は箱の右から最大値(=94)まで線分(ひげ)を引きます。
そして、箱の右側(第3四分位数の部分=84)から最大値(=94)まで線分を引きます。

箱ひげ図の書き方その5
箱ひげ図では、平均値を「+」で表記する場合があります。
平均値=(56+68+86+62+72+77+65+94+84+82)/10=74.6[点]ですね。
なので、74.6の位置に「+」を記載しましょう。

以上で箱ひげ図が完成しました。
四分位数と箱ひげ図の見方
では、箱ひげ図はどのように見れば良いのでしょうか?
例えば、以下の箱ひげ図を見てみましょう。
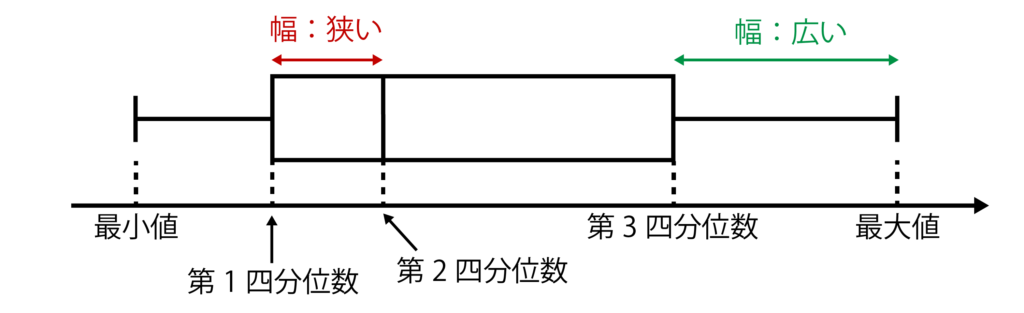
以上の箱ひげ図では第1四分位数と第2四分位数の間は狭くなっています。
つまり、この狭い幅の中に全データの約25%が入っているので、この部分にデータが集中しているということがわかるのです。
また、第3四分位数と最大値の間の幅は広くなっています。
つまり、この広い幅の中に全データの約25%が入っているので、この部分にデータが集中しているとは言えないということがわかるのです。
以上より、箱ひげ図においては、
- 幅が狭い=データが集中している(=「データの密度が高い」と言う)
- 幅が広い=データが集中しているとは言えない(=「データの密度が低い」と言う)
という法則があります。必ず覚えておきましょう。
いかがでしたでしょうか?
今回は四分位数とは何かについて解説した後、四分位数の求め方や第1四分位数・箱ひげ図との関係などについても解説してみました。
四分位数は冒頭でも解説した通り、データの分析や統計において重要な用語の1つです。ぜひ繰り返し本記事を読んで、内容をしっかりと理解してください。


