標準偏差という言葉を聞いたことがありますでしょうか?
標準偏差は分散と並んで紹介されることが多い用語で、高校数学の数学1における「データの分析」ではかなり重要な用語の1つとなっています。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が標準偏差とは何かについて解説します。また、標準偏差の求め方や計算方法・公式だけでなく、分散との関係などについても解説します。
数学やデータの分析に苦手意識がある人でも理解できるようにわかりやすく解説していくので、ぜひ最後までお読みください。
標準偏差とは?
中央値の周りのデータの散らばり具合を知るためには四分位偏差を使うのでした。
※詳しくは四分位数とは何かについて解説した記事をご覧ください。
それに対して、平均値の周りのデータの散らばり具合を知るためには標準偏差もしくは分散を使います。
標準偏差は分散の正の平方根の値となります。例えば、分散=100の場合、標準偏差=√100=10となります。
※平方根がわからない人は平方根とは何かについて解説した記事をご覧ください。
標準偏差も分散も、値が大きいほどデータがより散らばっていることを意味し、値が小さいほど平均値の周りにデータがより集中していることを意味するので覚えておきましょう。
標準偏差の求め方・計算方法・公式
先ほども解説した通り、標準偏差を求めるためには分散を求めなければなりません。
分散の求め方については分散とは何かについて解説した記事でご紹介しているので、詳しくはそちらをご覧いただくとして、本記事では簡単に分散・標準偏差の求め方をご紹介していきます。
【例題】
生徒が6人いるクラスで数学のテスト(10点満点)を実施した。生徒6人の点数が以下であるとき、この数学のテストの分散と標準偏差を求めよ。
| 点数 | 度数 |
|---|---|
| 7、10、9、8、8、6 | 6 |
※度数の意味がわからない人は度数分布表とは何かについて解説した記事をご覧ください。
【解答&解説】
まずはデータの平均値を求めます。
平均値=(7+10+9+8+8+6)/6=48/6=8ですね。
次は各データの偏差(=各データの値-平均値)を求めます。
各データの偏差を一覧にすると以下のようになりますね。
| 点数 | 偏差 |
|---|---|
| 7 | 7-8=-1 |
| 10 | 10-8=2 |
| 9 | 9-8=1 |
| 8 | 8-8=0 |
| 8 | 8-8=0 |
| 6 | 6-8=-2 |
偏差を求めたら、偏差平方(=偏差の平方のこと)を求めます。平方=2乗のことです。
各データの偏差を一覧にすると以下のようになりますね。
| 点数 | 偏差 | 偏差平方 |
|---|---|---|
| 7 | 7-8=-1 | 1 |
| 10 | 10-8=2 | 4 |
| 9 | 9-8=1 | 1 |
| 8 | 8-8=0 | 0 |
| 8 | 8-8=0 | 0 |
| 6 | 6-8=-2 | 4 |
ここまで来たら、次は偏差平方の平均を求めます。偏差平方の平均が分散に相当します。つまり、
分散=(1+4+1+0+0+4)/6=10/6=5/3・・・(答)となります。
また、上記でも解説した通り分散の正の平方根が標準偏差なので、
標準偏差=√5/√3=√15/3・・・(答)となります。
以上が標準偏差の求め方となります。たくさんの問題を解いていけば標準偏差の求め方は自然と身に付きますので、問題量をこなすことをぜひ意識してください。
標準偏差と単位の関係
分散でも平均値の周りのデータの散らばり具合を知ることができるのに、なぜわざわざ標準偏差も求める必要があるのでしょうか?
それは、もとのデータと単位を揃えるためです。
上記の例題を振り返るとわかりますが、分散を求める過程で偏差を平方(=2乗)しました。
偏差=各データの値-平均値なので単位は[点]ですが、偏差を平方することによって単位が[点2]になってしまいます。
[点]という単位は理解できますが、[点2]という単位は何を意味するのか不明ですね。
分散では単位がもとのデータの単位の2乗になってしまうという弱点があるので、単位をもとのデータと揃えるために標準偏差(=分散の正の平方根の値)を考えるのです。
標準偏差とデータの中心の傾向
ここからは「データの中心の傾向」という用語について解説していきます。
平均値-標準偏差 以上 平均値+標準偏差 以下にデータ全体の約68%が含まれている
という法則があります。これをデータの中心の傾向といいます。
四分位数の学習したにおいて、中央値の周辺におけるデータのばらつき具合を考えるとき、第1四分位数と第3四分位数の間にデータの約50%が含まれるという法則がありましたが、その平均値バージョンと考えていただければ問題ありません。
※中央値とは何かについて解説した記事もぜひ参考にしてください。
図で表現すると以下のようになります。
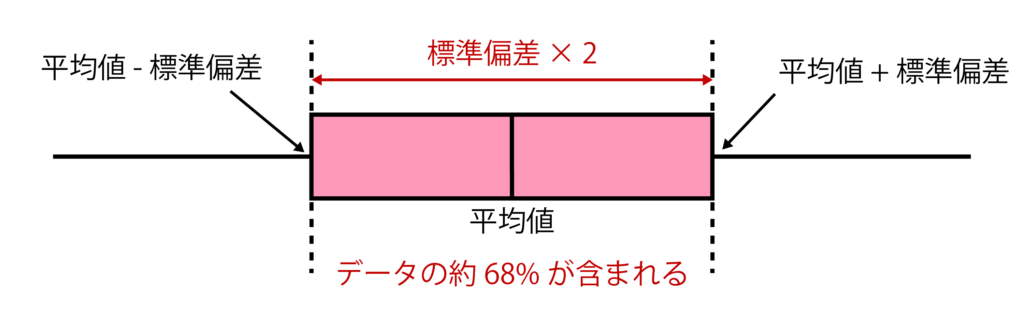
ちなみにですが、平均点-標準偏差×3〜平均点+標準偏差×3の間から外れた値は全体の傾向から外れたデータとします。つまり、かなり珍しいデータということになります。
では、データの中心の傾向に関する例題を1つ解いてみましょう。
【例題】
ある学校で数学のテストが行われた。この数学のテストを受験した生徒は全部で300人いる。
また、この数学のテストの平均点は60点、標準偏差は12点であることがわかっている。このとき、以下の問いに答えよ。
(1)データの中心の傾向を求めなさい。
(2)データの中心に含まれる生徒は約何人か求めなさい。
【解答&解説】
(1)データの中心の傾向は「平均値-標準偏差 以上 平均値+標準偏差 以下」なので、
60-12以上60+12以下より、48点以上72点以下・・・(答)となります。
(2)(1)より、48点以上72点以下の間に全体の約68%が含まれるので、
300×68%=300×0.68=204となるので、答えは約204[人]・・・(答)となります。
ちなみにですが「60-12×3から60+12×3の間」つまり「24点から96点の間」に入っていない人は全体のデータから外れたデータになるので、かなり珍しい点数となります。
標準偏差と偏差値
最後に標準偏差と偏差値の関係について解説します。
模試などで偏差値という言葉がよく登場しますが、偏差値とはその人の点数が受験者全体の中でどれくらいの位置にいるかを数値化したものです。
偏差値は(得点-平均点)/標準偏差 ×10 +50で求めることができます。
例えば、平均点=60点、標準偏差=30点の100満点のテストがあったとします。
このテストでA君が90点を取ったとします。
すると、A君の偏差値=(90-60)/30 ×10+50=10+50=60となります。
偏差値に関しては、受験者の上位の約2%が偏差値70以上となり、上位の約16%が偏差値60以上となります。
つまり、100人の受験者がいたら上から約2番目までが偏差値70以上、上から約16人番目までが偏差値60以上となります。
東大や京大などの偏差値70以上というのがいかにすごいことかよくわかりますね。
今回は標準偏差とは何か・求め方や計算方法、分散との関係などについて解説しました。
標準偏差は数学1「データの分析」の中でもかなり肝となる用語の1つです。分散と一緒に必ず計算できるようにしておきましょう。


