平方根は簡単に言えば√(ルート)のことです。大学入試や共通テストでは√が登場する問題は必ず出題されるので、平方根に関する知識は必須です。
そこで本記事では、早稲田大学教育学部数学科を卒業した筆者が、平方根とは何か・求め方についてわかりやすく解説します。また、平方根の計算方法や平方根を利用した図形問題などもご紹介していきます。
平方根に関して充実の内容となっていますので、ぜひ最後までお読みください。
平方根とは?わかりやすく解説
まずは平方根とは何か?平方根の定義からわかりやすく解説していきます。
2乗するとaになる数を、aの平方根といいます。平方根は2乗根とも呼ばれていますが、一般的には平方根がよく使われるので平方根で覚えておけば問題ありません。
例えば、2乗すると100になる数は10と-10ですね。なので、100の平方根は10と-10になります。
10と-10をまとめて±10と表記します。
一般的に、正の整数aの平方根は√aと-√aの2つがあります。まとめて±√aと表記します。
ちなみに、0の平方根は0だけであり、√0=0となります。
記号「√」は日本語で根号と呼ばれます。
数学1で学習する実数の範囲には負の数の平方根は存在しません。例えば、-100の平方根を考えたとき、2乗して-100になる数は存在しません。
※実数とは何かについて解説した記事もぜひ合わせてご覧ください。
数学2で「虚数」という概念を学習すれば負の数の平方根も求めることができますが、本記事では割愛させていただきます。
平方根の性質と絶対値の関係
ここからは平方根の性質をご紹介します。
覚えておきたい性質は以下の2つです。
性質1
a≧0のとき、(√a)2=a、(-√a)2=a、√a≧0 である。
例を使って考えてみましょう。例えば、a=100とします(100>0ですね)
すると、(√100)2=102=100となり、aと等しくなっています。
(-√100)2=(-10)2=100となり、これもaと等しくなっています。
また、√100=10なので、0よりも大きくなっていることが確認できます。
性質2
a≧0のとき、√a2=aである。
また、a<0のとき、√a2=-aである。
すなわち、√a2=|a|となる。
こちらもa=100で考えてみましょう(100≧0ですね)
a=100のとき、√a2=√10000=100(=a)となっていることがわかります。
√1002=|100|となっていることも確認できます。
次はa=-100で考えてみましょう(-100<0ですね)
こちらは、√(-100)2=√10000=100(=-a)となっていることがわかります。
※aではなく、-aになっていることに注意してください。
√a2の取り扱いには注意が必要で、機械的に√a2=aとするのは絶対にNGです。
a<0かどうかで必ず場合分けをするようにしましょう。
√(-100)2=|-100|になっていることも確認できます。
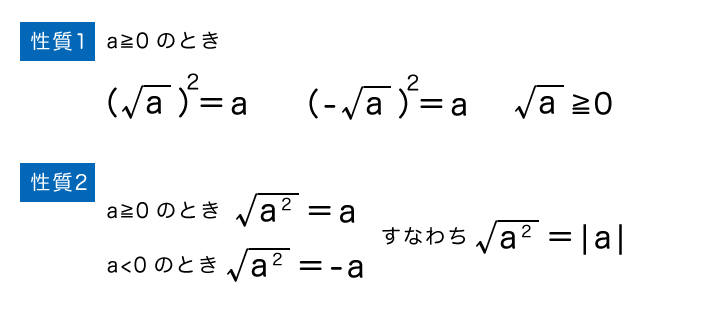
平方根の計算方法
平方根の計算では、以下3つの公式が登場しますので覚えておきましょう。
a>0、b>0、k>0のとき、
- √a √b = √ab
- √a / √b = √(a/b)
- √k2a = k√a
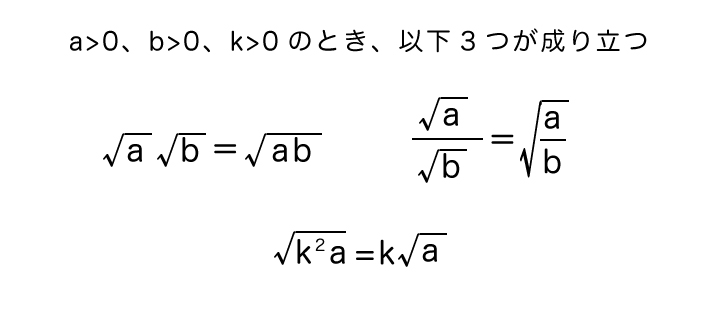
順番に詳しくみていきましょう。
まず、√a √b = √abですが、例えば、√3 × √2 = √2×3 = √6となります。
この式が成り立つことを証明するには、(√a √b)2を考えてみます。
(√a √b)2=(√a)2(√b)2となり、先ほど解説した平方根の性質1より、(√a)2=a、(√b)2=bなので、(√a)2(√b)2=abとなります・・・(✳︎)
(√a √b)2=(√a)2(√b)2が成り立つ理由については多項式の計算について解説した記事をご覧ください。
また、√a>0、√b>0なので√a √b > 0となります。
よって、√a √bはabの正の平方根であり、√a √b=√ab となります。
2つ目の√a / √b = √(a/b)ですが、例えば、√10 / √5 = √(10/5)=√2となります。
証明ですが、(✳︎)と同様に考えて、(√a/ √b)2=a/b、√a / √b > 0から、√a / √b = √a/bとなります。
√k2a = k√aは、例えば√32a=3√aになるということです。
証明ですが、a>0、k>0であるから、1と2より、√k2a=√k2√a=k√aとなります。
平方根と分母の有利化
分母に根号を含む式を変形して、分母に根号を含まない式にすることを「分母を有理化する」といいます。
分母の有理化には、
- (√a)2=a
- (√a+√b)(√a-√b)=a-b
を利用します。例えば、1/√aを有理化することを考えてみましょう。
分子・分母に√aをかけてみます。すると、√a/(√a)2=√a/aとなり、分母に根号を含まない式に変形できました。これで分母の有理化が完了です。
次は、1/(√a+√b)を有理化することを考えてみます。
次は分子・分母に(√a-√b)をかけましょう。すると、(√a-√b)/(a-b)となるので、こちらも分母に根号を含まない式に変形でき、分母の有理化が完了しました。
定期テストや大学入試、共通テストなど数学の試験においては、答えは分母の有理化を行うのが一般的なので、有理化の方法は必ず覚えておきましょう。
平方根の近似値
√2や√5など、高校数学でよく使う数字の近似値(=おおよその数のこと)は覚えておくと便利です。
有名な語呂合わせがあるので、覚えておきましょう。
√2=1.41421356(ひと夜ひと夜に人見ごろ)
√3=1.7320508(人並みに奢れや)
√5=2.2360679(富士山ろくオーム鳴く)
√6=2.449489(煮よ。よく弱く)
√7=2.6457513(菜に虫いない)
※「菜」は√7の「7」を指しています。
√8=2.828(ニヤニヤ)
平方根の練習問題
最後に、平方根の練習問題を解いてみましょう。
平方根を活用した図形問題も用意しているので、ぜひチャレンジしてみてください。
【練習問題1】
以下の値を計算しなさい。
(1)√(-6)2
(2)√(-8)(-2)
(3)√a2b2(a>0、b<0とする)
(4)(√15-√3)(√15+√3)
(5)(√2+√3)2
【解答&解説】
(1)√(-6)2=|-6|=6・・・(答)
(2)√(-8)(-2)=√16=4・・・(答)
(3)√a2b2=√(ab)2=|ab|
a>0、b<0より、ab<0です。よって-ab・・・(答)
(4)(√15-√3)(√15+√3)
=15-3
=12・・・(答)
(5)(√2+√3)2
=(√2)2+2 × √2 × √3 +(√3)2
=2+2√6+3
=5+2√6・・・(答)
【練習問題2】
以下の式に関して、分母の有理化を行いなさい。
(1)4/√6
(2)1/(√3+√6)
(3)4/(1+√2+√3)
【解答&解説】
(1)4/√6
=4√6 / (√6)2
=4√6 / 6
=2√6 / 3・・・(答)
(2)1/(√3+√6)
=1(√3-√6)/(√3+√6)(√3-√6)
=(√3-√6)/3-6
=-(√3-√6)/3
=(√6-√3)/3・・・(答)
(3)分母・分子に(1+√2-√3)をかけると上手くいきます。
4/(1+√2+√3)
=4(1+√2-√3)/(1+√2+√3)(1+√2-√3)
=4(1+√2-√3)/{(1+√2)2-(√3)2}
=4(1+√2-√3)/2√2
ここから、さらに分母・分子に√2をかけて有理化します。
4(1+√2-√3)×√2 / 2(√2)2
=4(√2+2-√6)/4
=2+√2-√6・・・(答)
【練習問題3】
以下の(1)〜(3)について、√(a-1)2+√(a-3)2の根号を外して簡単にしなさい。
(1)a>3
(2)1≦a<3
(3)a<1
【解答&解説】
(1)√(a-1)2+√(a-3)2=|a-1|+|a-3|・・・(✳︎)となりますね。
a>3なら、a-1>0、a-3>0なので、
(✳︎)=(a-1)+(a-3)=2a-4・・・(答)となります。
(2)1≦a<3のとき、a-1≧0、a-3<0なので、
(✳︎)=(a-1)-(a-3)=2・・・(答)となります。
(3)a<1のとき、a-1<0、a-3<0なので、
(✳︎)=-(a-1)-(a-3)=-2a+4・・・(答)となります。
【練習問題4】
半径10cmの円がある。その円の中に、できるだけ大きな正方形を作ることを考える。このとき、正方形の1辺の長さは何cmになるか求めなさい。
【解答&解説】
円の中にできるだけ大きな正方形を作る場合、以下の図のように円の直径が正方形の対角線になるようにすれば良いですね。
円の直径(正方形の対角線)によって正方形が2分割されて、同じ形の直角二等辺三角形が2つ登場していることに注目しましょう。
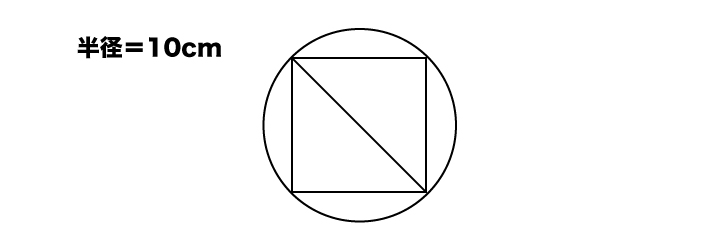
斜辺=20cmより、求める正方形の1辺の長さ=20 / √2 =10√2・・・(答)となります。
いかがでしたでしょうか?
今回は平方根とは何かについて解説した後、平方根の計算方法や分母の有理化、平方根の近似値などをご紹介しました。
繰り返しにはなりますが、試験で解答を記載するときは分母の有理化をするのが一般的です。分母の有理化は必ずマスターしておきましょう。


