sin225度の値を求めようとしたとき、自分で直角三角形を書いてその値を求めようとしてもできません。
なので、sin225度を求めるには単位円を活用するのが一般的です。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin225度の求め方について数学が苦手な人でも理解できるようにわかりやすく解説していきます。
sin225度の値は暗記するのではなく、必ず自力で求められるようにしておきましょう。
※三角比(sin・cos・tan)の求め方がわからない人は三角比の覚え方について解説した記事をまずはお読みください。
sin225度の求め方
冒頭でも述べた通り、sin225度のようにsinθのθ>90度の場合は単位円を使ってその値を求めるのが定石です。
単位円は大学入試や共通テストでも頻出であり、非常に便利なツールなので必ず使えるようにしておきましょう。
※単位円=xy平面上において原点Oを中心とした半径1の円のこと。単位円上の任意の点Pの座標を(x、y)とするとsinθ=y、cosθ=xとなるのでした(以下の図参照)
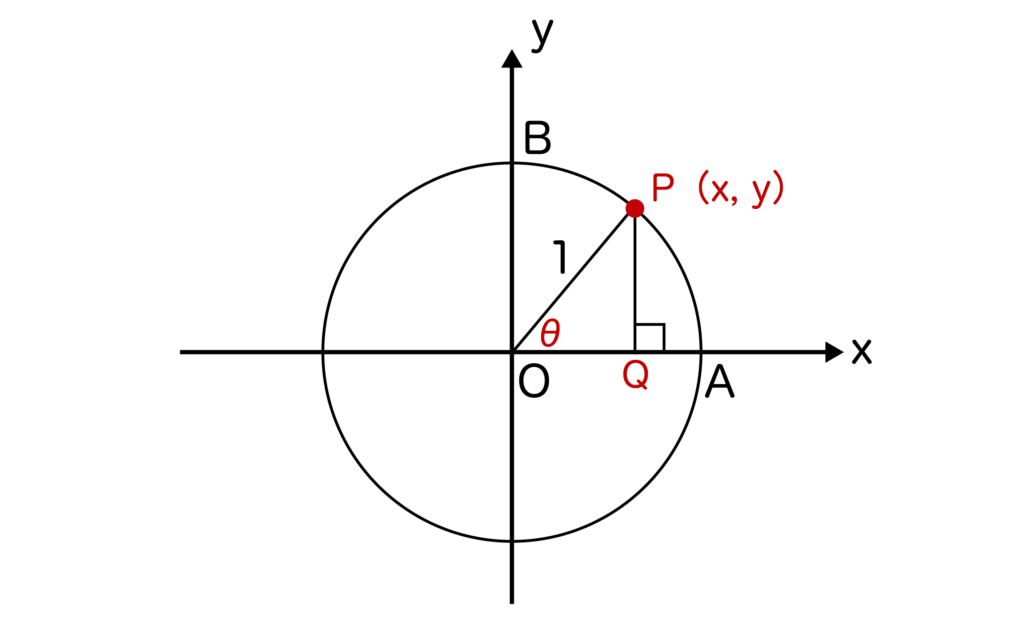
※sinθ=y、cosθ=xになる理由についてはsin90度が1なのはなぜかについて解説した記事をご覧ください。
今回はsin225度の値を求めるので、θ=225度となります。θ=225度を単位円上に取ると以下のようになりますね。
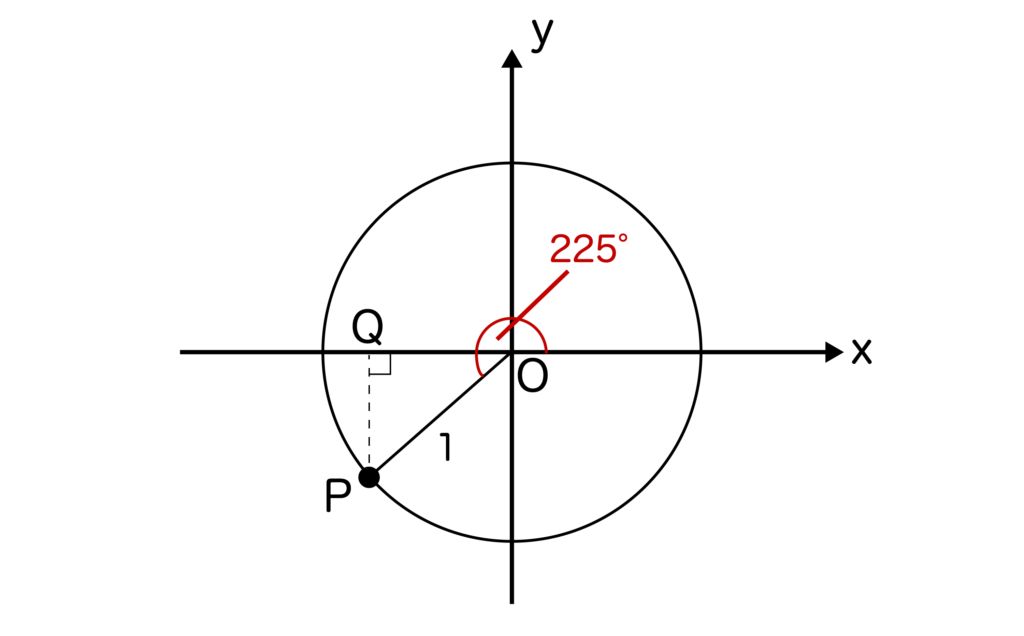
上記の図のように、点Pからx軸に対して下ろした垂線の足とx軸との交点をQとします。
すると、∠POQ=225度-180度=45度となるので、三角形OPQは45度型の直角三角形であることがわかります。
つまり、PQ:PO:=1:√2となりますね。単位円であることから、OP=1なので、PQ=1/√2となります。
したがって、点Pのy座標は-1/√2となりますね(マイナスが付くことにご注意ください)
以上より、sin225度=点Pのy座標=-1/√2となります。
sin225度を加法定理で求めてみる
先ほどはsin225度を単位円を使って求めましたが、加法定理を使ってsin225度を求めることも可能です。
※加法定理をまだ学習していない人は飛ばしていただいて大丈夫です。
225度=180度+45度に注目します。すると加法定理より、
sin225度=sin(180度+45度)=sin180度・cos45度+cos180度・sin45度=0・1/√2+(-1)・1/√2=-1/√2となります。
※sin180度の求め方について解説した記事やsin45度の求め方について解説した記事もぜひ合わせてご覧ください。
単位円を使って求めたsin225度の値と確かに一致していることがわかります。
加法定理も大学入試・共通テストで頻出です。単位円・加法定理どちらも使えるようにしておきましょう。
sin225度のとき、cos225度とtan225度は?
最後にcos225度とtan225度の値も求めておきましょう。
cos225度は先ほど利用した単位円を使って求めてみます。

三角形OPQは45度型の直角三角形であり、OP=1なので、OQ=1/√2です。
つまり、点Qのx座標は-1/√2となります。
単位円においてはsinθ=y(点Pのy座標)、cosθ=x(点Pのx座標)であることから
sin225度=点Pのx座標=点Qのx座標=-1/√2となります。
続いてtan225度ですが、tanθ=sinθ/cosθより、
tan225度=sin225度/cos225度=-1/√2 ÷ (-1/√2)=1となります。
※tanθ=sinθ/cosθがわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
以上をまとめると、
- sin225度=-1/√2
- cos225度=-1/√2
- tan225度=1
となります。θ=225度のときはsinとcosの値は同じになるのですね。
今回はsin225度の値を2通りの方法(単位円・加法定理)で求めてみました。
繰り返しにはなりますが、単位円も加法定理ともに三角関数の学習において非常です。必ず使いこなせるようにしておきましょう。