sin30度が分数で1/2になる理由を2通りで超丁寧に解説

sin30度は分数で1/2となりますが、1/2になる理由をしっかりと説明できますでしょうか？

sin30度＝1/2とただ単に暗記しているだけではこの先の三角関数の学習で必ずつまずいてしまうので、これを機に必ずsin30度が1/2になる理由を説明できるようにしておきましょう。

そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin30度＝1/2になる理由を2通りの方法（図形・単位円）で解説していきます。

特に単位円はこの先の三角関数の学習でも登場するので必ずチェックしておきましょう。

sin30度が分数で1/2になる理由（図形を書く）

まずは自分で図形を書いてsin30度の値を求めてみましょう。

以下の図ように、左下の角度＝30度の直角三角形ABCを書いてみます。

※三角比（sin・cos・tan）を図形をもとに考えるときは左下に対象の角度を持ってくるとわかりやすいです。詳しくは三角比の覚え方について解説した記事をご覧ください。

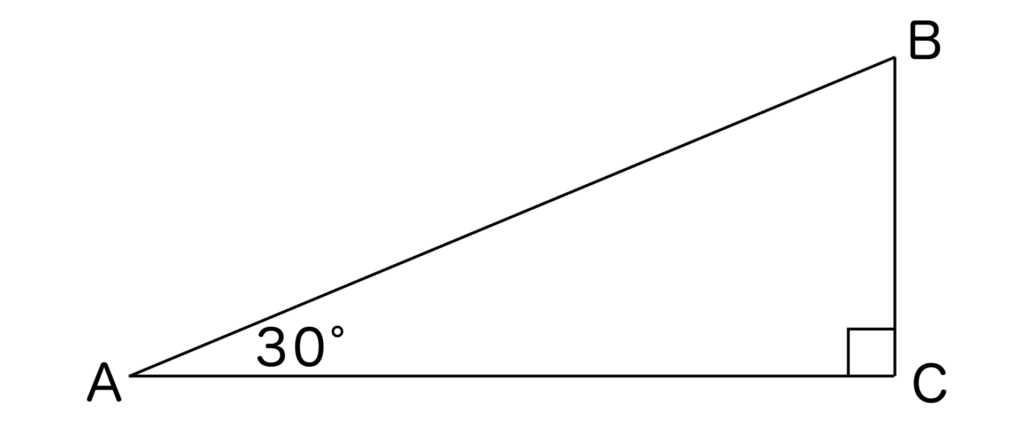
すると、∠＝60度であることがわかるので、BC：AB：AC ＝1：2：√3となりますね。

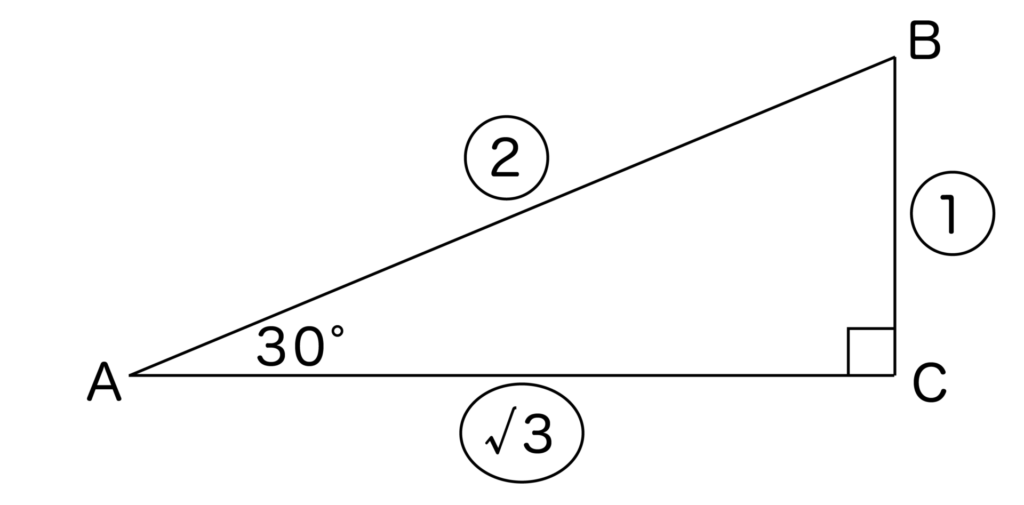
よって、sin30度＝BC/AB＝1/2となることがわかります。

三角比（sin・cos・tan）を求めるときは辺の長さ（10cmなど）を活用する必要はありません。辺の比さえわかっていればそれを活用して三角比（sin・cos・tan）は求めることが可能です。

例えば、上記の直角三角形ABCにおいてAB＝20cm、BC=10cm、AC=10√3cmとします。

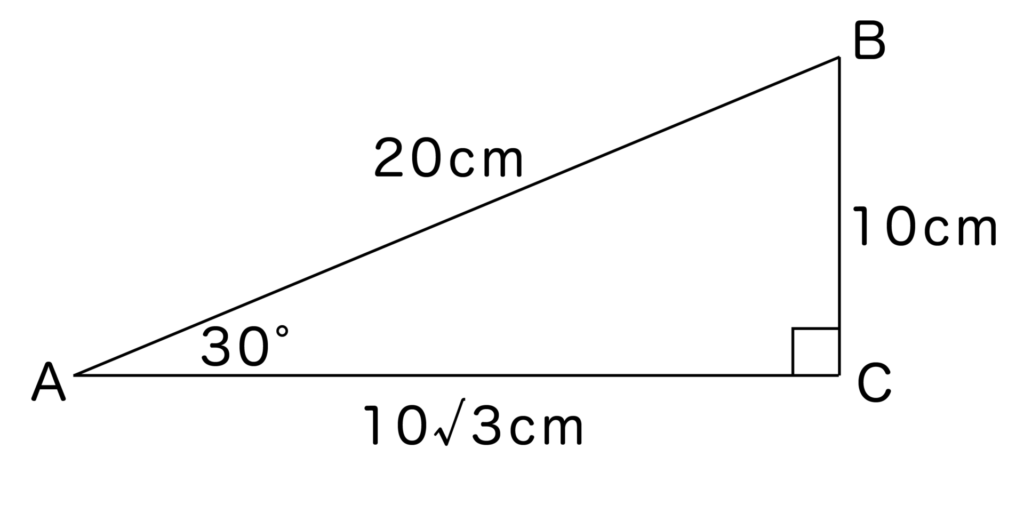
すると、sin30度＝BC/AB＝10cm/20cmで確かに1/2になっていることがわかります。

最終的には約分することになるので、三角比（sin・cos・tan）を求めるときは辺の比を活用するのがおすすめです。

次は単位円を使ってsin30度＝1/2になる理由を解説していきます。

単位円とは単位円とはxy平面上において点Oを中心とした半径＝1の円のことで、点P（x、y）を単位円上に取ると、sinθ＝y、cosθ＝xになるのでした。

※sinθ＝y、cosθ＝xが成り立つ理由についてはsin90度が1なのはなぜかについて解説した記事をご覧ください。

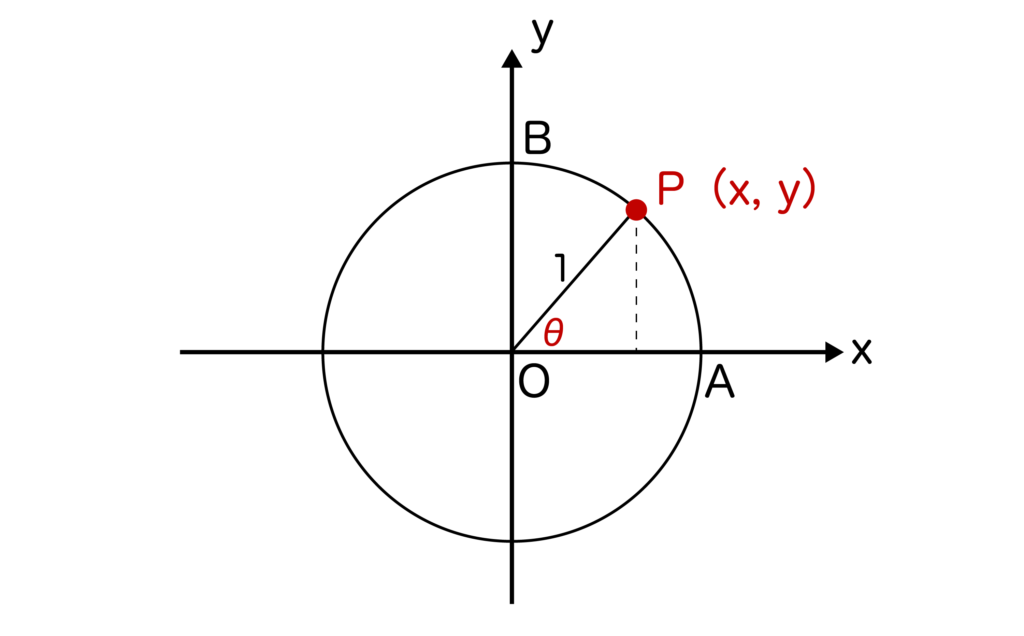
この単位円においてθ＝30度を作り、点Pからx軸に下ろした垂線とx軸との交点を点Qとします。

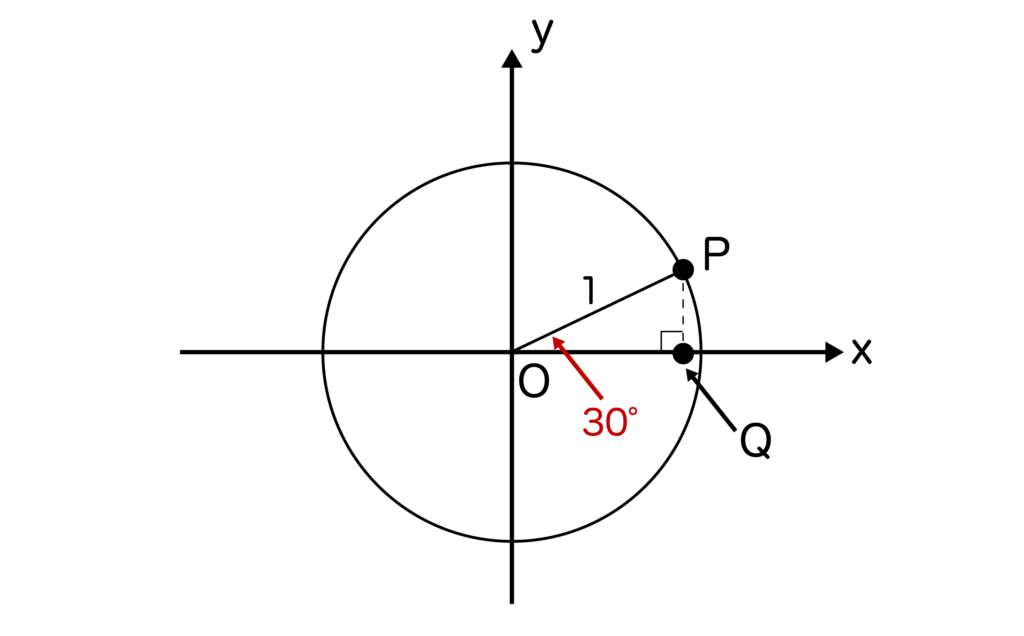
すると、∠QOP＝30度の直角三角形OPQが完成しました。

単位円なので、OP=1です。すると、OP：PQ＝2：1よりPQ=1/2となりますね。

したがって、sin30度＝PQ/OP＝1/2となります。

以上が単位円を活用したsin30度の求め方になります。単位円は大学入試や共通テストでも頻出なので、いつでも活用できるようにしておきましょう。

以上でsin30度＝1/2になる理由を解説していきましたが、念のため以下の三角比の表でsin30度が1/2になっているか確認しておきましょう。赤枠で囲った部分がsin30度の値となります。

※三角比の表の見方を解説した記事もご用意しているので、三角比の表の見方がわからない人はぜひ参考にしてください。

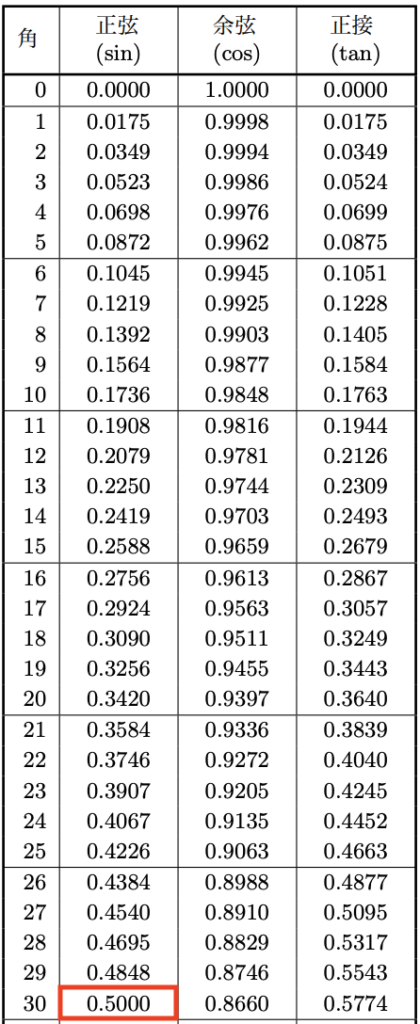
sin30度＝0.5000となっており、0.5000は分数に直すと1/2なので、sin30度は確かに1/2であることが確認できました。

sin30度＝1/2のときのcos、tanの値も念のため求めておきましょう。

もちろん上記でご紹介した図を書く or 単位円を活用してcos30度、tan30度を求めても良いですが、今回はあえて三角比の関係式・相互関係の公式を使って求めてみます。

sin²θ＋cos²θ＝1より、（1/2）²＋（cos30度）²＝1となるので、（cos30度）²＝3/4となります。

cos30度>0より、cos30度＝√3/2となります。

※cos30度>0になる理由ですが、θ＝30度の単位円を書いてみると以下のようになり、単位円においてはcosθ＝xなのでcos30度＝点Qのx座標となります。点Qのx座標は明らかに正なので、cos30度>0となります。

また、tanθ＝sinθ/cosθより、tanθ＝1/2 ÷ √3/2＝1/√3となります。

以下の直角三角形ABCを見ても、確かにcos30度＝AC/AB＝√3/2、tan30度＝BC/AC＝1/√3となっていることが確認できます。

今回はsin30度が分数で1/2になる理由について図を書くパターンと単位円を使うパターンの2つで解説していきました。

特に単位円は非常に便利で、sinθ＝y、cosθ＝xは暗記必須です。必ず使えるようにしておきましょう。