sinθ=1やsinθ=1/2のθを皆様はスムーズに求めることができますでしょうか?
後ほど詳しく解説しますが、θの値を求めるには単位円を使うのが定石です。
本記事では早稲田大学教育学部数学科を卒業した筆者がsinθ=1やsinθ=1/2の求め方を図解でわかりやすく解説していきます。
数学が苦手な人でも理解できるように解説しているので、ぜひ最後までご覧ください。
sinθ=1のときのθの求め方
まずはsinθ=1のときのθを求めてみましょう。
冒頭でも解説した通り、三角比(sin・cos・tan)においてθを求めるときは単位円を使うのが定石です。
※三角比の求め方がわからない人は三角比の覚え方について解説した記事をご覧ください。
単位円とはxy平面において原点Oを中心とした半径=1の円のことです。そして、単位円上に点P(x、y)を取ると、sinθ=y、cosθ=xが成り立つのでした(以下の図参照)
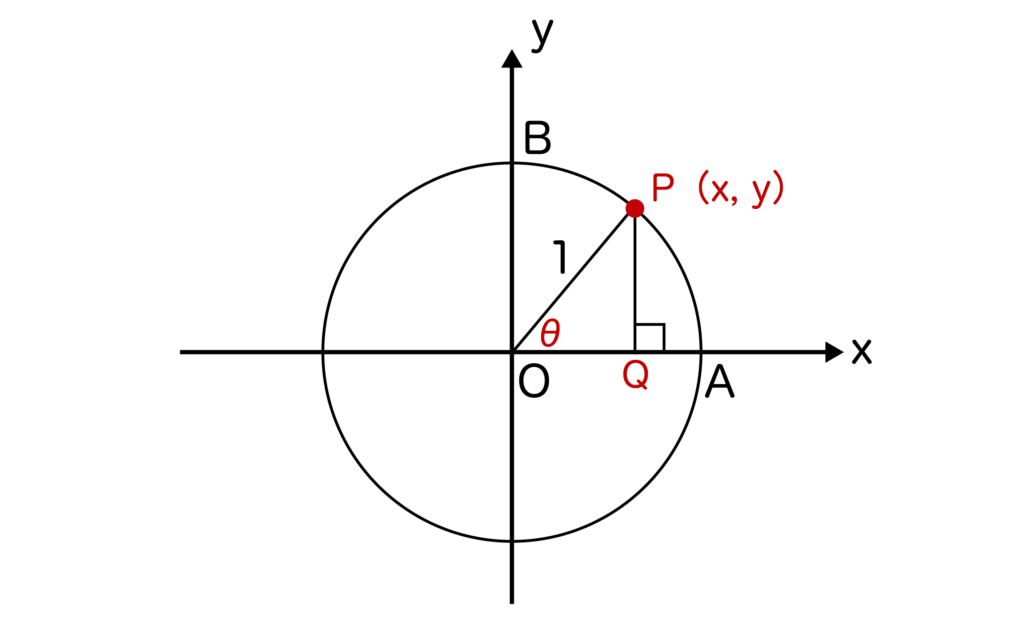
※sinθ=y、cosθ=xが成り立つ理由がわからない人はsin90度が1なのはなぜかについて解説した記事をご覧ください。
なので、sinθ=1を求める方法としては、まずはy=1を単位円上に引いてみます。
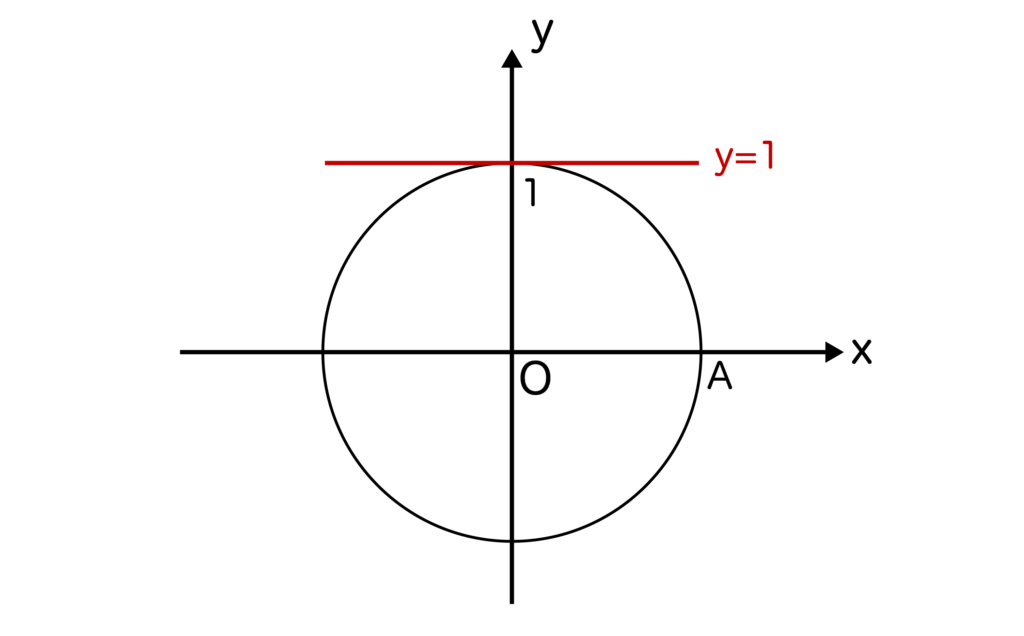
そして、y=1と単位円の交点を点Pとします。今回はy=1と単位円は1点でしか交わりませんね。
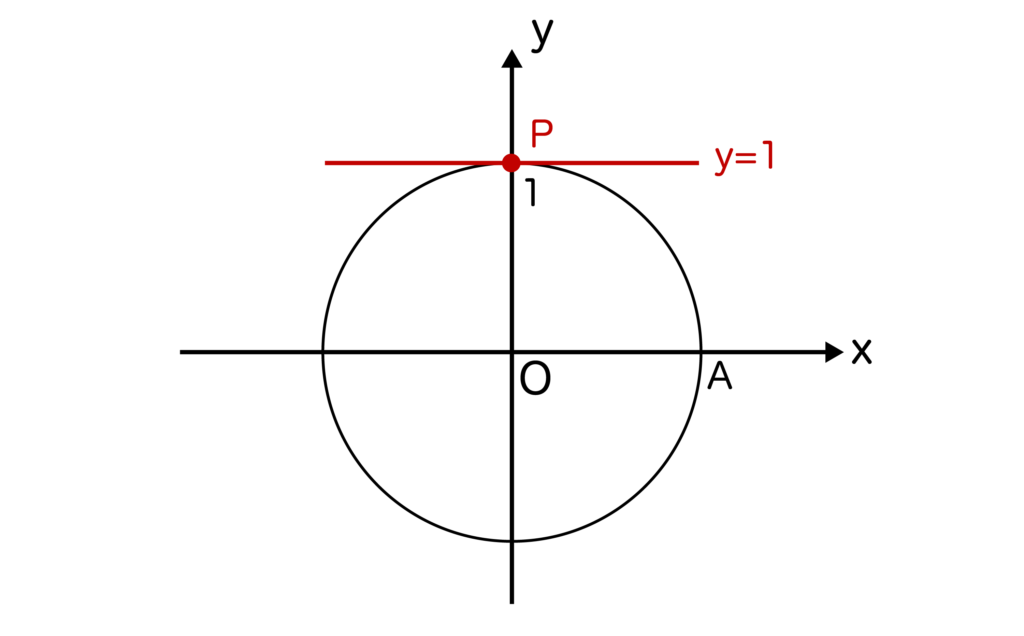
点Pの座標は(0、1)となり、∠AOP=90度となるので、θ=90度となります。
以上がsinθ=1のときのθの求め方となります。
sinθ=aという式が出てきたら、sinなのでy=aを単位円上に引く→単位円とy=aの交点を調べて角度を求めるという流れを必ず理解しておきましょう。
sinθ=1/2のときのθの求め方
先ほどと同様の流れで今度はsinθ=1/2のときのθを求めてみましょう。
sinなのでy=1/2を単位円上に引き、単位円とy=1/2との交点をそれぞれP、Qとします。
そして、点P、Qからx軸に対して下ろした垂線とx軸との交点をそれぞれA、Bとします。
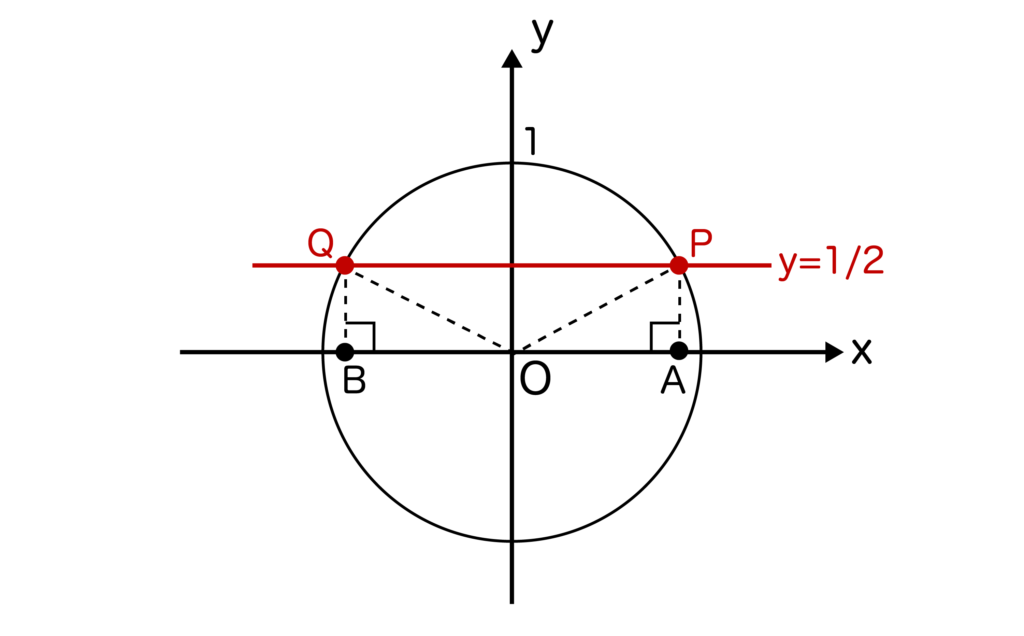
すると、単位円であることからOP=OQ=1です。そして、y=1/2なのでAP=BQ=1/2です。
つまり、三角形OAP、三角形OBQはともにOP:AP=OQ:BQ=2:1の直角三角形であることがわかります。
したがって、∠AOP=BOQ=30度となります。
以上より、求めるθ=∠AOPと∠AOQとなるのでsinθ=1/2を解くとθ=30度、150度となります。
※sin30度が分数で1/2になる理由について解説した記事もぜひ合わせてご覧ください。
以上が単位円を使ったsinθ=1/2の求め方です。手順はsinθ=1のときと変わりません。
単位円は大学入試や共通テストでも頻出なので、必ず使えるようにしておきましょう。
sinθ=1、sinθ=1/2のとき、cosθとtanθの値は?
- sinθ=1のときθ=90度
- sinθ=1/2のときθ=30度、150度
となりました。ついでにcos90度、cos30度、cos150度とtan90度、tan30度、tan150度の値も求めておきましょう。
すると、
- cos90度=0
- cos30度=√3/2
- cos150度=-√3/2
ですね。
ここで、tan90度、tan30度、tan150度の求め方ですがtanθ=sinθ/cosθの公式を使いましょう。
※tanθ=sinθ/cosθがわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
よって、
- tan90度=sin90度/cos90度=1/0=計算不可(tan90度はなぜ値がないかについて詳しく解説した記事もぜひ合わせてご覧ください。)
- tan30度=sin30度/cos30度=1/2 ÷ √3/2=1/√3(tan30度の求め方について解説した記事もぜひ合わせてご覧ください)
- tan150度=sin150度/cos150度=1/2 ÷ (-√3/2)=-1/√3
となります。
※tan90度=計算不返に関してですが、分数において分母=0は高校数学では認められていません。ある数を0で割ることはできないためです。分子=0は問題ありません。
tanθ=sinθ/cosθも単位円と同じくらい非常に重要なので必ず覚えておきましょう。
いかがでしたか?
今回はsinθ=1やsinθ=1/2の求め方を解説していきました。
単位円においてはsin=y、cos=xです。呪文のように唱えていつでも使いこなせるようにしておきましょう。