sin180度の求め方とsin(180度-θ)＝sinθになる理由をわかりやすく解説

皆様はsin180度の値をパッと求めることができますか？

sin180度の値は暗記しても問題はありませんが、今後の三角関数の学習を踏まえるといつでも自力で求められるようにしておかなければなりません。

しかし、自力でどうやってsin180度の値を求めれば良いのかわからない高校生も多いのではないでしょうか？

そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin180度の求め方を数学が苦手な人向けにわかりやすく解説します。

また、sin180度に関して知っておきたい知識としてsin（180度-θ）＝sinθになる理由も解説していきますので、ぜひ最後までご覧ください。

sin180度の求め方

sin180度を求めるには単位円を使うのが良いでしょう。

単位円とはxy平面上において原点Oを中心とした半径1の円のことで、単位円においてはsinθ＝y、cosθ＝xが成り立つのでした（以下の図参照）

※単位円上の任意の点Pからx軸に対して下ろした垂線とx軸との交点をQとすると、sinθ＝PQ/OP＝PQ＝y、cosθ＝OQ/OP＝OQ＝xとなることがわかります（sin、cosの求め方がわからない人は三角比の覚え方について解説した記事をご覧ください）

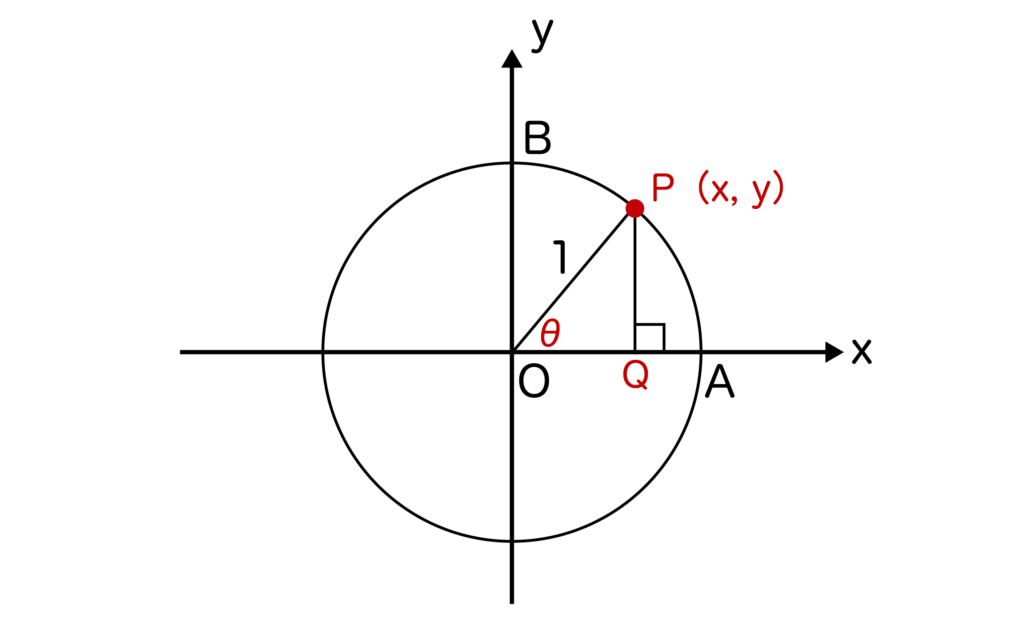
そして、単位円においては上記の図でいうところのOAをθ＝0度とし、θが正の場合はOAを起点に反時計回りに角度を取るのでした。

今回はsin180度の値を求めるので、θ＝180度です。θ＝180度を単位円上に取ると以下のようになりますね。

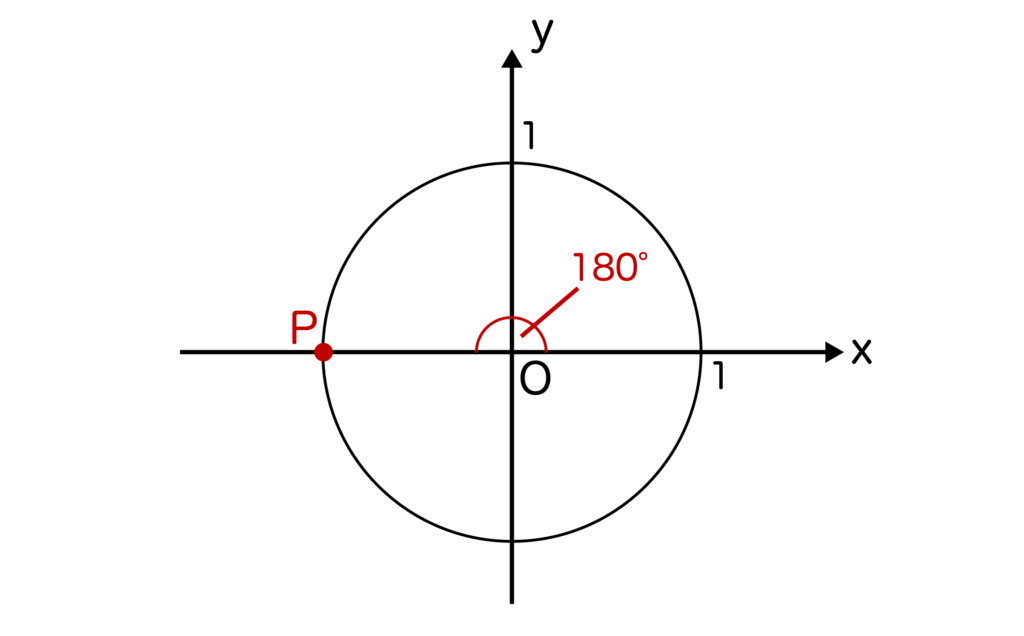
つまり、点Pはx軸と単位円の交点（-1、0）となります。

先ほども解説した通り、単位円においてはsinθ＝y（点Pのy座標）、cosθ＝x（点Pのx座標）となるので、sin180度＝点Pのy座標＝0となります。

以上が単位円を利用したsin180度の求め方です。特に、sinθ＝y、cosθ＝xは非常に重要なので必ず覚えておきましょう。

sin180度の値は2倍角の公式を使って求めることも可能です。

2倍角の公式とは以下の公式のことでした。

※2倍角の公式をまだ習っていない人は本章をスキップして問題ありません。

sin2α=2sinαcosα

180度＝2×90度なので、sin180度＝2・sin90度・cos90度＝2・1・0＝0となります。

2倍角の公式も単位円と同じくらい重要ですので、必ず覚えておきましょう。

sin180度に関して知っておきたい知識としてはsin（180度-θ）＝sinθの公式があります。

例えば、sin30度を考えてみます。30度＝180度-150度なので、上記の公式に当てはめてみるとsin（180度-150度）＝sin150度となります。

実際に、sin（180度-150度）=sin30度＝1/2ですね。

そして、sin150度も以下の図の通り、単位円を使って考えてみると1/2になることがわかります。

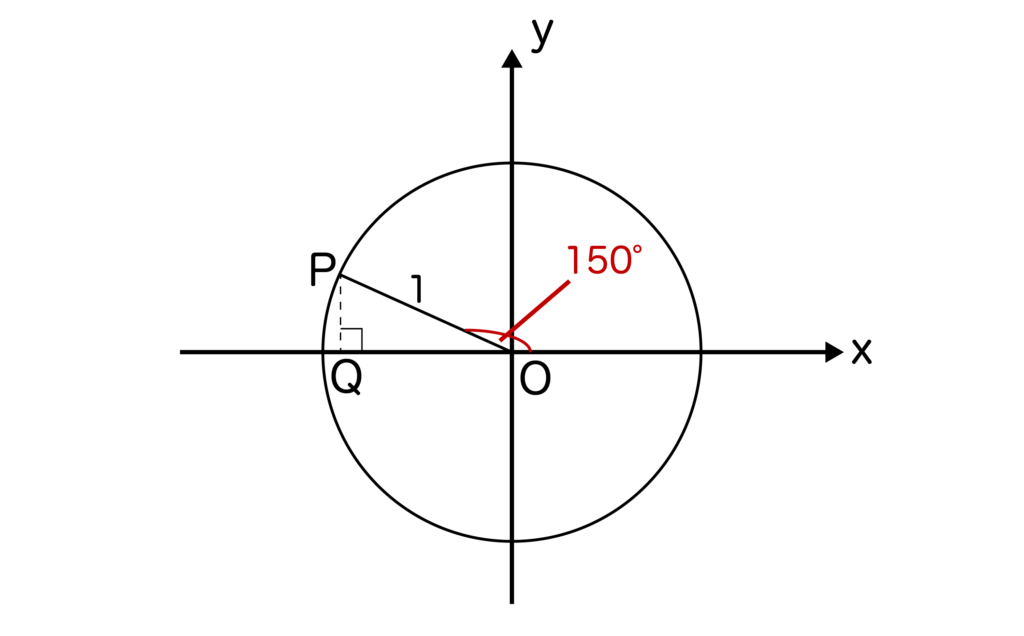
したがって、sin（180度-150度）＝sin150度は確かに成り立っています。

sin（180度-θ）＝sinθが成り立つ理由は加法定理を使うことで証明できます。

加法定理より、sin（180度-θ）＝sin180度・cosθ-cos180度・sinθ＝0・cosθ-（-1）・sinθ＝sinθとなり、sin（180度-θ）＝sinθが証明できました。

sin（180度-θ）＝sinθは大学入試や共通テストでもよく利用するので、公式として覚えてしまいましょう。

先ほどsin180度＝0を求めましたが、ついでにcos180度とtan180度も求めてみましょう。

まずはcos180度からです。再び単位円上にθ＝180度を取ります。

sinθ=y、cosθ=xより、cos180度＝点Pのx座標＝-1となることがわかります。

続いてtan180度ですが、これはtanθ＝sinθ/cosθを使います。

※tanθ＝sinθ/cosθがわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。

tan180度＝sin180度/cos180度＝0/-1＝0となります。

分数において分子＝0は問題ないですが、分母＝0になることはありませんのでご注意ください。数を0で割ることはできません。

以上をまとめると、sin180度＝0、cos180度＝-1、tan180度＝0となります。

いかがでしたでしょうか？今回はsin180度の求め方とsin（180度-θ）＝sinθが成り立つ理由、cos180度およびtan180度の求め方について解説しました。

sin180度は暗記するだけでなく、なぜ0になるのか？をしっかり説明できるようにしておきましょう！