sin90度が1なのはなぜ？誰でもわかるように超わかりやすく解説！

高校数学1の鬼門とも言える三角関数ですが、皆様はsin90度＝1になる理由を説明できますでしょうか？

sin90度＝1は暗記しても良いのですが、三角関数をこれから深く学習していくならばsin90度＝1になる理由は必ず説明できるようにしておかなければなりません。

そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin90度＝1になるのはなぜなのか？について誰でもわかるように解説していきます。

三角関数が苦手な人にとっても非常に重要なことなので、ぜひ最後までご覧ください。

sin90度＝1になるのはなぜ？（単位円）

sin90度が1になる理由は単位円を使って説明することができます。

単位円とはxy平面上において原点Oを中心とした半径＝1の円のことです。

このとき、点P（x、y）を単位円上に取ると、sinθ＝y、cosθ＝xになります。

※単位円においてはAOをθ＝0度とします。sin、cosがわからない人は三角比の覚え方について解説した記事をご覧ください。

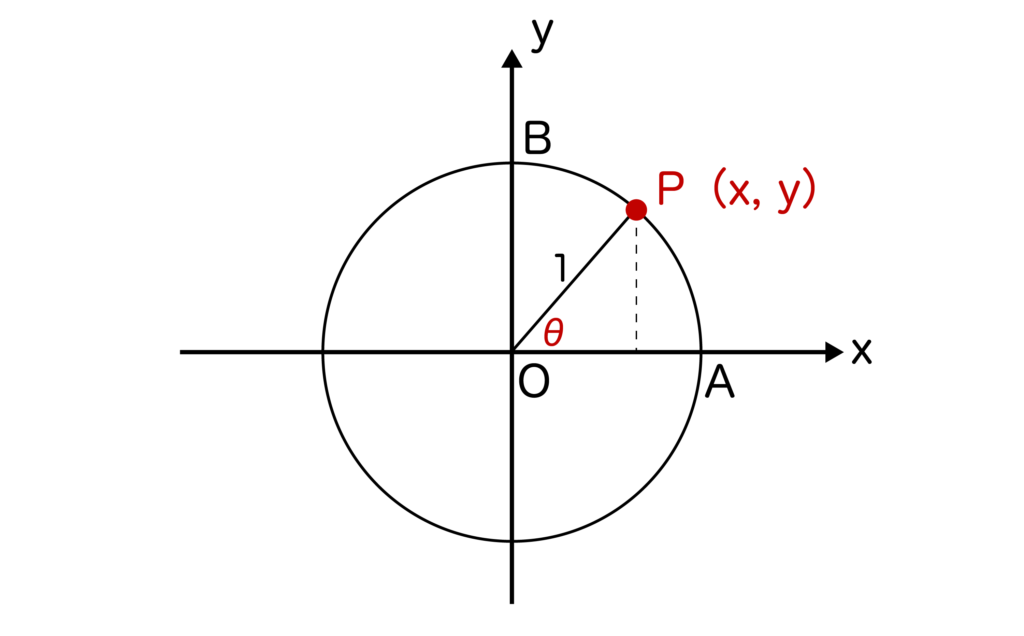
「sinθ＝y、cosθ＝x」は非常に重要なので必ず覚えておきましょう。

sinθ＝y、cosθ＝xになる理由ですが、単位円の半径＝1よりsinθ＝y/1＝y、cosθ＝x/1＝xとなるからです。

では、以上をもとにしてsin90度を考えてみましょう。

90度ということは∠AOB＝90度ということですね。

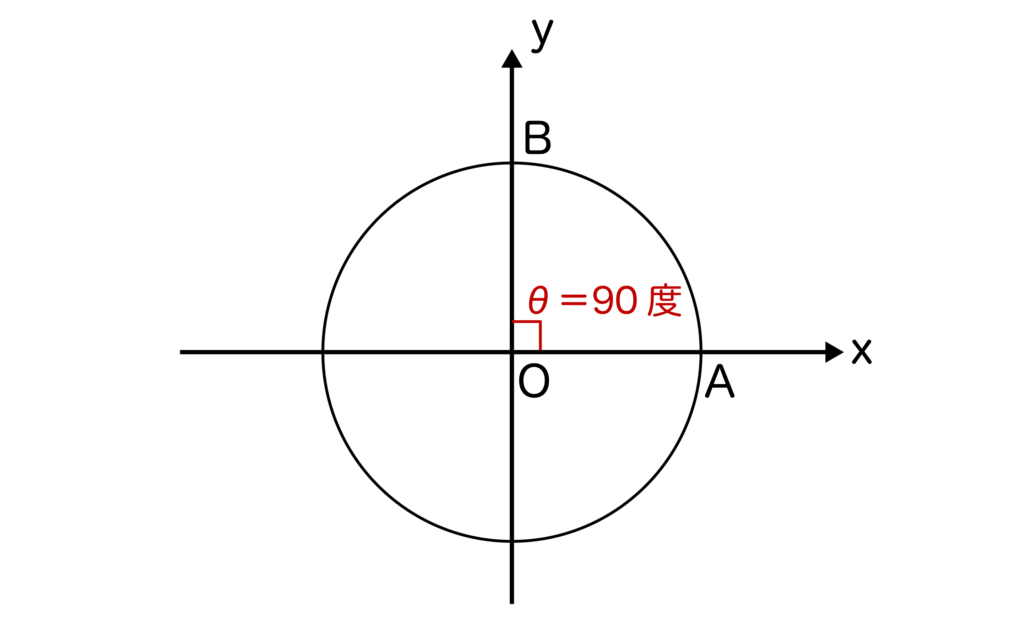
sinθ＝yなので、sin90度＝点Bのy座標＝1となることがわかります。

以上がsin90度＝1となる理由です。

単位円を使って三角比（sin・cos・tan）を考える手法は大学入試や共通テストでもよく登場するので、必ずできるようにしておきましょう。

では、sin90度＝1のときcos90度、tan90度の値はいくつになるか求めてみましょう。

sin²θ＋cos²θ＝1より、（sin90度）²＋（cos90度）²＝1²＋（cos90度）²＝1となるので、（cos90度）²＝0となります。

したがって、cos90度＝0となります。

※sin²θ＋cos²θ＝1が成り立つ理由がわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。

ちなみにですが、cos90度に関してはsin²θ＋cos²θ＝1を使わなくても、上記で解説した通り単位円においてcosθ＝xであることを使っても問題ありません。

θ＝90度ということは∠AOB＝90度となり、cos90度＝点Bのx座標となるので確かに0となっていることが確認できます。

では、tan90度はどうでしょうか？

tanθ＝sinθ/cosθより、tan90度＝sin90度/cos90度＝1/0となり、計算不可となります。

※分数においては分母≠0でした。分母＝0の場合は計算不可となります。

よってtan90度の値はなしとなるのでご注意ください。

いかがでしたでしょうか？今回はsin90度が1なのはなぜなのかについて解説していきました。

単位円において「sin＝y、cos＝x」は非常に重要です。三角比の公式の1つとして必ず覚えておきましょう！

※sin30度が1/2になる理由について解説した記事もご用意しているので、ぜひ参考にしてください。