皆様はsin45度の値を即答できますでしょうか?sin45度は1/√2となります。
中にはsin45度の値を暗記していて即答できる人もいるかもしれませんが、重要なのはなぜsin45度は1/√2なのかを説明できることです。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin45度の求め方を2通り解説していきます。
三角関数が苦手な人はぜひ最後まで読んでいただき、なぜsin45度が1/√2になるのかを理解しましょう。
sin45度の求め方その1
sin45度の求め方1つ目は、自分で45度の直角三角形を書くというやり方です。
左下に45度がくるように直角三角形ABCを書いてみると以下のようになりますね。
※中学数学で学習しましたが、45度の直角三角形の辺の比は1:1:√2でした。
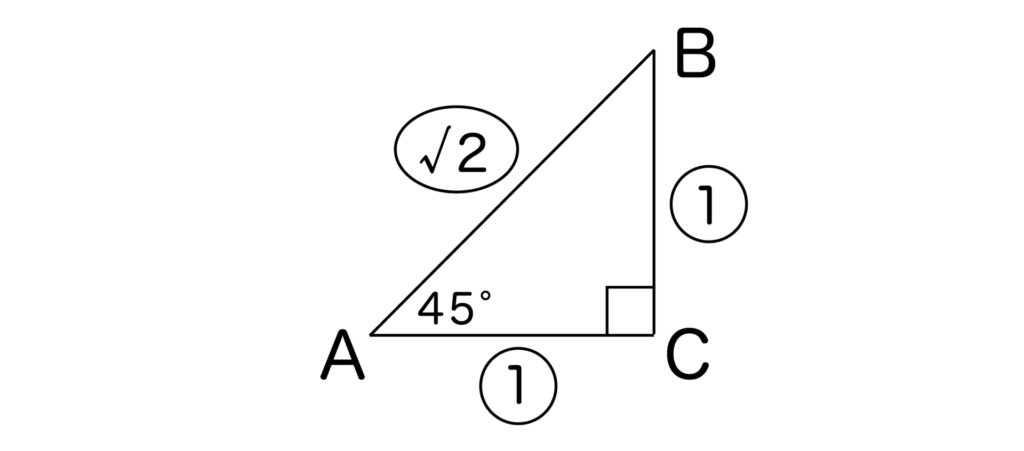
したがって、sin45度=BC/AB=1/√2となります。
※sin45度=BC/ABになる理由がわからない人は三角比の覚え方について解説した記事をご覧ください。
以上がsin45度の求め方としては最も簡単な方法になります。1分もかからずに求めることができるでしょう。
自分で図形を書いて三角比(sin・cos・tan)を求めるという方法はもちろん45度だけではなく30度や60度などでも使えますので、必ずできるようにしておきましょう。
※sin30度が分数で1/2になる理由について解説した記事もご用意しているので、ぜひ参考にしてください。
sin45度の求め方その2
sin45度の求め方2つ目は単位円を活用する方法です。
単位円とはxy平面上において原点Oを中心とした半径=1の円のことです。点P(x、y)を単位円上に取ると、sinθ=y、cosθ=xになります。
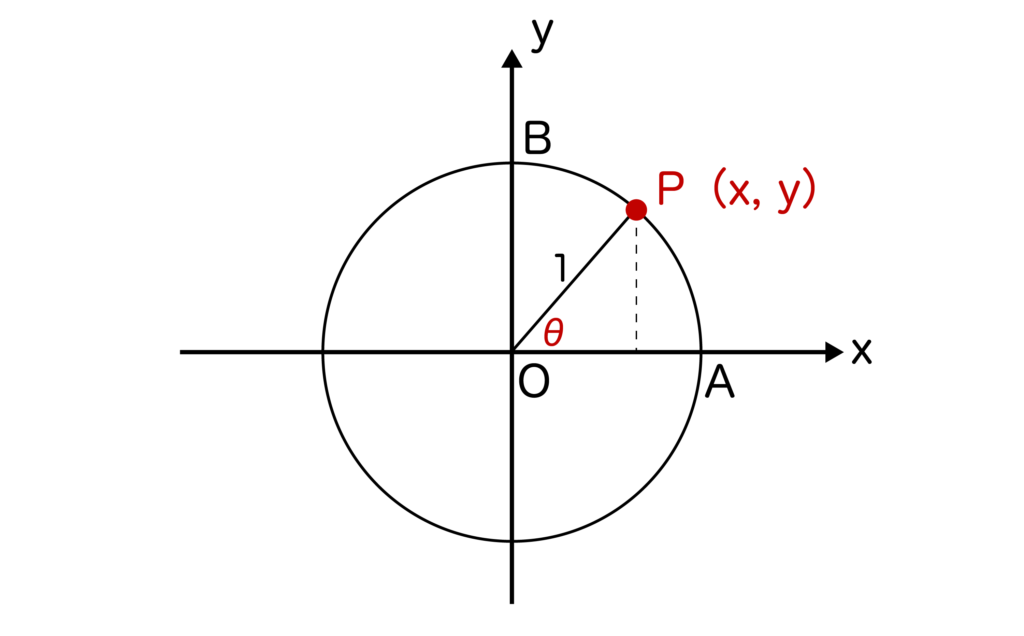
※sinθ=y、cosθ=xになる理由についてはsin90度が1なのはなぜかについて解説した記事をご覧ください。
今回はsin45度の値を求めるので、単位円上にθ=45度をとります。すると、以下のようになりますね。
※点Pからx軸に対して下ろした垂線とx軸との交点を点Qとします。
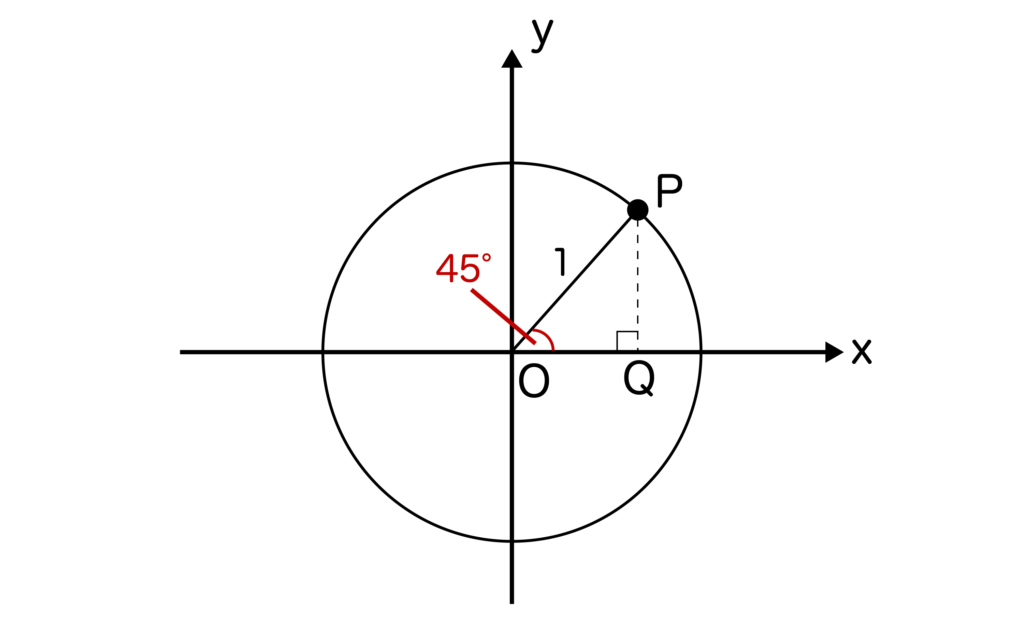
すると、三角形OPQは45度の直角三角形なので、PQ:OP=1:√2となります。
ここで、単位円なのでOP=1となることから、PQ:1=1:√2より、PQ=1/√2が求まります。
したがって、sin45度=PQ/OP=1/√2となります。
以上が単位円を使ったsin45度の求め方になります。
1つ目にご紹介した自分で45度の直角三角形を書いてsin45度を求めるときよりは少し手間がかかりますが、単位円の使い方に慣れるという意味ではこの方法もぜひ理解しておきましょう。
この先、三角比の学習を進めていくにあたって単位円は非常に重要になってきます。
sin45度を三角比の表で確認してみよう。
以上でsin45度=1/√2が証明できましたが、念のため三角比の表でsin45度の値も確認しておきましょう。
以下の赤枠の通り、三角比の表ではsin45度=0.7071となっています。
※表の見方がわからない人は三角比の表の見方について解説した記事をご覧ください。
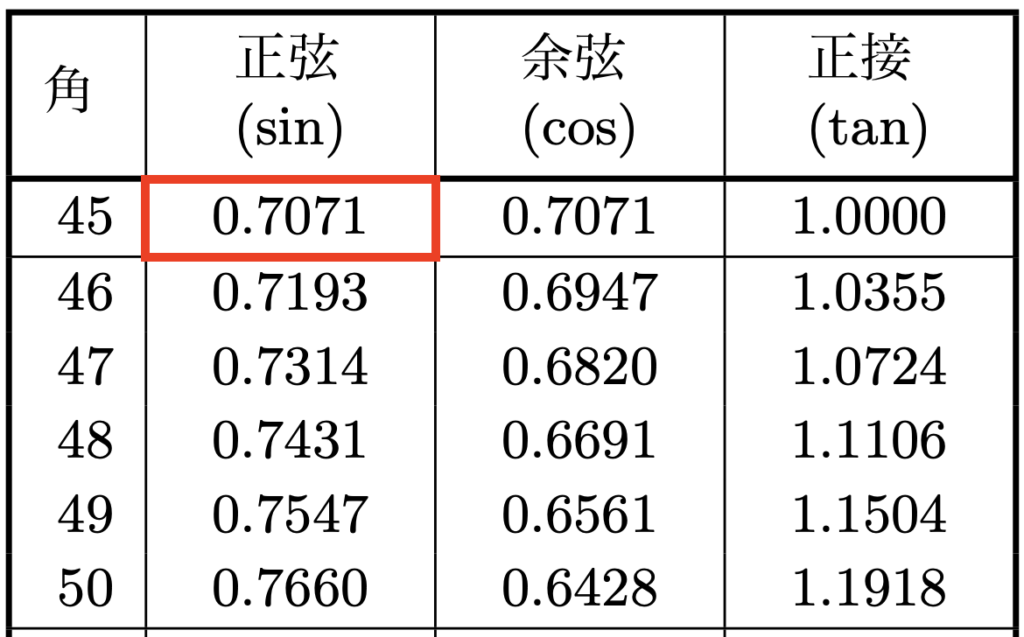
√2=1.41421356(ひと夜ひと夜に人見ごろ)なので、1/√2=0.70710678…となります。
※√2の近似値は「ひと夜ひと夜に人見ごろ」という語呂合わせが有名ですが、√3や√5にも語呂合わせがあります。詳しくは平方根とは何かについて解説した記事をご覧ください。
したがって、sin45度は確かに1/√2であることが確認できました。
三角比の表は大学入試や共通テストではあまり使う機会はありませんが、表の見方はとても簡単なのでぜひ覚えておきましょう。
【おまけ】cos45度、tan45度はどうなる?
sin45度の値は無事求めることができましたが、最後におまけとしてcos45度とtan45度の値も求めておきましょう。
先ほどと同様に、また以下のような45度の直角三角形を書きます。

すると、cos45度=AC/AB=1/√2、tan45度=BC/AC=1となることがわかります。
sin45度とcos45度は同じ値となりますので覚えておくと便利です。
いかがでしたか?今回はsin45度の求め方について解説していきました。
繰り返しにはなりますが、自分で図形を書いて三角比を求めるのが最も手っ取り早い方法です。ぜひ他の角度でも試してみてください。