高校数学の数学1では実数という概念が登場します。しかし、実数の定義をしっかりと覚えている人は少ないのではないでしょうか?
実数は高校数学では非常に重要な概念の1つなので、必ず理解しておかなくてはなりません。
そこで今回は、実数とは何か・定義について早稲田大学教育学部数学科を卒業した筆者がわかりやすく簡単に解説します。また、0は実数?整数は実数?有理数は実数?など実数に関するよくある質問にも回答しています。
実数とは?定義をわかりやすく・簡単に解説
まずは実数とは何か?実数の定義についてわかりやすく・簡単に解説します。
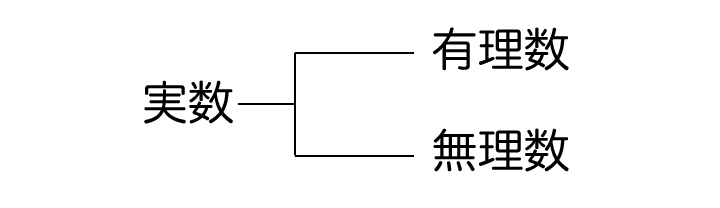
実数とは有理数と無理数の総称です。つまり、実数は有理数と無理数で構成されているということです。
ここからは、有理数・無理数について詳しく解説していきます。
有理数とは?
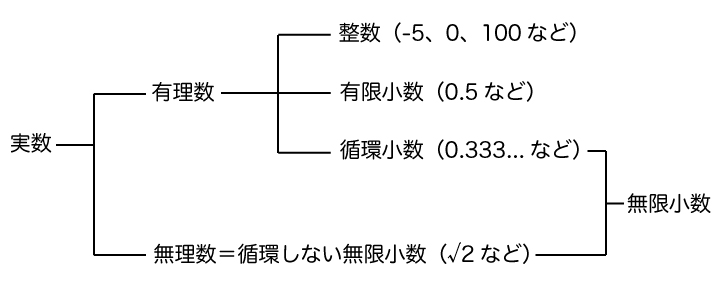
有理数とは、整数・有限小数・循環小数のことです。
有理数は必ず分数m/nで表すことができます(mは整数・nは0でない整数とする)
整数は-10、-6、0、5、100など小数や分数ではない数のことです。ちなみに、1以上の整数のことを自然数と呼ぶのでした。
整数である5は5/1、10は10/1、-100は-100/1のように表すことができるので有理数となります。
有限小数は1.74、5.5、-0.93など終わり(1.74の場合は4で終わっている)が決まっている小数のことです。
終わりが決まっている小数は必ず分数m/nで表すことができるので有理数となるわけです。
それに対して、終わりが決まっておらず、小数点以下が循環する小数のことを循環小数と言います。
例えば、1/3を小数にすると0.3333…となり3が永遠に続きます(=循環します)
1/9は0.1111…となり1が永遠に続きます(=循環します)
循環小数も分数m/nで表すことができるので有理数となります。
※有理数について詳しく解説した記事もや循環小数について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
無理数とは?
無理数とは終わりが決まっておらず、小数点以下が循環しない小数のことです。
例えば、円周率は3.1415926535…と小数点以下が法則性なく永遠に続く(=循環しない)ので無理数となります。
また、√2=1.41421…とこちらも小数点以下が法則性なく永遠に続くので無理数となります。
※循環しない無限小数と先ほどご紹介した循環小数を合わせて無限小数と言います。
しかし、√(ルート)が付く数字すべてが無理数というわけではないのでご注意ください。
例えば、√9=3となるので無理数ではなく有理数となります。
以上をまとめると、以下のようになります。
- 実数は有理数と無理数にわけられる
- 有理数は整数・有限小数・循環小数にわけられる
- 無理数とは、循環しない無限小数のことである
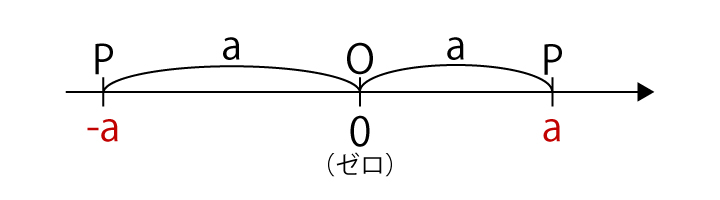
実数は数直線上の点で表すことができる
すべての実数は数直線上の点で表すことができます。
直線上に基準となる点Oをとり、単位の長さと正の向き(=通常は右向き)を定めます。点Oには実数0(ゼロ)を対応させます。
そして、この直線上の点Pに対して以下のように実数を対応させることができます。
- 点Pが点Oの右側に存在し、OPの長さがaのとき、正の実数a
- 点Pが点Oの左側に存在し、OPの長さがaのとき、負の実数-a
以上のように、直線上の各点に1つの実数を対応させるとき、この直線のことを数直線と言います。また、点Oは原点と呼ばれます。
実数に0は含まれる?マイナスの数は?
ここからは、実数に関するよくある質問をご紹介していきます。
【Q1】0(ゼロ)は実数ですか?
【A】はい、実数です。先ほども解説した通り、0は整数の1つであり、有理数なので実数となります。
【Q2】マイナスの数は実数ですか?
【A】はい、実数です。ただし、マイナスの数が有理数か無理数かは判断が必要です。分数で表現できるマイナスの数(例:-10、-3.56)は有理数ですが、-1.6482…など循環しないマイナスの無限小数の場合は無理数となります。
【Q3】整数・自然数は実数ですか?
【A】はい、ともに実数です。自然数は1以上の整数のことを指し、有理数に該当するので実数となります。
実数はRで表現される
実数は英語でReal Numberと呼ばれます。この頭文字を取って、実数はRと表現されるケースもあります。
例えば、自然数100は実数に該当するので、100∈Rのように表記されます。これは「100はR(実数)に含まれる」を意味しています。
Rの他には自然数=N(Natural number)、整数=Z(ドイツ語でZahlen)、有理数=Q(英語で和差積商の「商」を意味するQuotient)などがあります。
大学入試や共通テストなどで問われることはないので、特に暗記する必要はありません。
実数解を持つとは?
実数の文脈で実数解という言葉があります。
実数解とは二次方程式の解が実数であり、かつ異なる2つの値であるものをいいます。
例えば、二次方程式x2−x−6を解いてみましょう。
x2-x-6を因数分解すると(x+2)(x-3)となるので、答えは-2と3になりますね。
※因数分解のやり方がわからない人は数学1の因数分解について解説した記事をご覧ください。
-2も3もともに実数であり、かつ異なる値なので実数解と言えます。
実数解の他には二重解と虚数解がありますが、それは数学2で学習する内容のため、本記事では割愛させていただきます。
※二重解について詳しく解説した記事もご用意しているのでぜひ参考にしてください。
実数の対義語「虚数」とは?
実数の対義語は「虚数」です。虚数とは実数ではない数のことです。
虚数は「i」を使って表され、i2=-1となります。
ちなみに、実数と虚数を組み合わせたものを複素数といいます。例としては、3+iや7-iなどがあげられます。
虚数の詳細は数学2で学習する内容のため、本記事では割愛させていただきます。
実数に関する練習問題
最後に実数に関する練習問題を2つご紹介します。両方とも超基礎的な問題なので、必ず解けるようにしましょう。
【練習問題1】
次の数を有理数と無理数に分類せよ。
-7、9、1.7、3/5、0.972、√100、-√3、π
【解答&解説】
有理数=-7、9、1.7、3/5、0.972、√100
無理数=-√3、π
√100=10なので有理数となります。上記でも解説しましたが、√(ルート)が付く=無理数ではないのでご注意ください。
【練習問題2】
数直線上で、次の点A・B間の距離を求めよ。
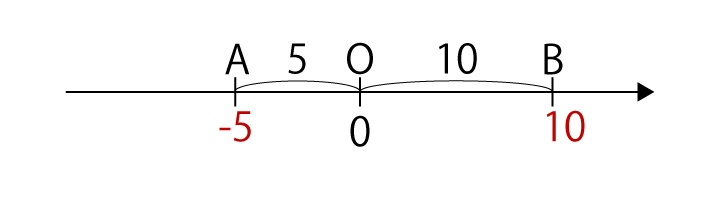
(1)A(-5)、B(10)
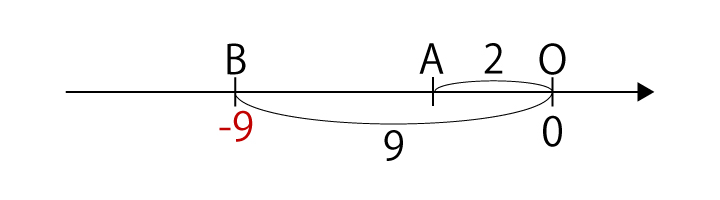
(2) A(-2)、B(-9)
【解答&解説】
(1)以下の図より、AB間の距離は15・・・(答)となります。
(2)以下の図より、AB間の距離は7・・・(答)となります。
今回は実数とは何か・定義について解説した後、実数と数直線の関係やR、虚数などをご紹介していきました。
数学2で虚数が登場するまでに目にする数字はすべて実数となります。虚数を学習したら虚数以外はすべて実数と覚えておけば特に問題はないでしょう。