高校数学の数学1では二次関数の前座的な役割として、一次関数の解説が教科書などで掲載されていることが多いので、本サイトでも解説することにします。
一次関数は中学数学でも学習した内容ですが、変化の割合や傾きなど重要用語も多いので改めてこれを機に復習しましょう。
※一次関数とは何かについて解説した記事もぜひ合わせてご覧ください。
本記事では早稲田大学教育学部数学科を卒業した筆者が一次関数の変化の割合・傾きとは何か、求め方について図解で解説していきます。
数学が苦手な人でも理解できるように解説してるので、ぜひ最後までお読みください。
一次関数の変化の割合・傾きとは?
まずは一次関数の変化の割合・傾きについて解説します。
変化の割合とはxが1増加したときに、yがどれだけ増加(または減少)するかを示したものです。
例えば、y=3x+5という一次関数があったとします。
x=1のとき、y=3×1+5=8ですね。ここで、xが1増加したときのyの増加量を考えてみましょう。
xが1増加すると、x=2となりますね。
x=2のとき、y=3×2+5=11ですね。
よって、yの増加量は11-8=3となります。
以上より、y=3x+5の変化の割合は3となります。
また、一次関数y=ax+bにおいて、aのことを「傾き」または「比例定数」と呼ぶのでした。
※比例定数とは何かについて詳しく解説した記事もぜひ合わせてご覧ください。
先ほど例にあげたy=3x+5の変化の割合は3で、これはy=3x+5の傾きと同じ値になっていますが、これは偶然ではありません。
一次関数においては変化の割合=傾き(=比例定数)となります。
傾きはxの値が1増加したときに、yの値がどれだけ増加するのかを示したものでした。
なので、傾きは変化の割合と同じ意味となるのです。
しかし、変化の割合=傾きとなるのは一次関数の場合のみとなるのでご注意ください。
※高校数学の数学1では二次関数を学習しますが、二次関数では傾きという概念は登場しません。
一次関数の変化の割合・傾きの求め方
ここからは、一次関数の変化の割合の求め方について解説していきます。
先ほども解説した通り、一次関数における変化の割合=傾きとなるので、変化の割合を求めるということは傾きを求めるのと同じです。
変化の割合を求めるには、以下2つのパターンがあります。
傾きがすでにわかっている場合
一次関数の傾きがすでにわかっている場合は変化の割合は1秒で求めることができます。
何度も解説している通り、変化の割合=傾きだからです。
例題を1つみてみましょう。
【例題】
一次関数y=-10x+4の変化の割合はいくつか答えよ。
【解答&解説】
傾きがすでに-10とわかっているので、変化の割合=-10となります。
傾きがわかっていない場合
傾きがわかっていない場合は傾きを求める必要があります。例題をみてみましょう。
【例題】
点(2,12)と点(5,18)を通る一次関数の変化の割合を求めよ。
【解答&解説】
変化の割合はyの増加量 / xの増加量で求めることができます。
(2,12)と(5.18)において、yの値は12から18に増加しているので、yの増加量=18-12=6です。
同様に考えてxの増加量は5-2=3です。
よって、変化の割合=6/3=2となります。
ちなみに、(2,12)と(5,18)を通る一次関数の式を連立方程式を使って解いてみましょう。
求める一次関数をy=ax+bとおくと、
- 12=2a+b・・・①
- 18=5a+b
より、-6=-3aとなるので、a=2となります。
a=2を①に代入して、12=4+bとなるので、b=8となります。
よって、(2,12)と(5,18)を通る一次関数はy=2x+8となります。
確かに傾きが2となっており、変化の割合と等しいことが確認できます。
※上記の通り、変化の割合だけを求めるのであればわざわざ連立方程式を解く必要はありません。
yの増加量 / xの増加量の公式をしっかりと使えるようにしておきましょう。
一次関数の変化の割合・傾きが大きいとグラフは急になる
ここからは、一次関数における変化の割合(傾き)とグラフについて解説していきます。
変化の割合の絶対値が大きいほど、一次関数のグラフは急になります。
例えば、y=2x+1とy=5x+1を比較してみましょう。
y=2x+1は変化の割合(傾き)の絶対値=2で、y=5x+1は変化の割合(傾き)の絶対値=5なので、以下の図のようにy=5x+1の方がグラフが急になります。
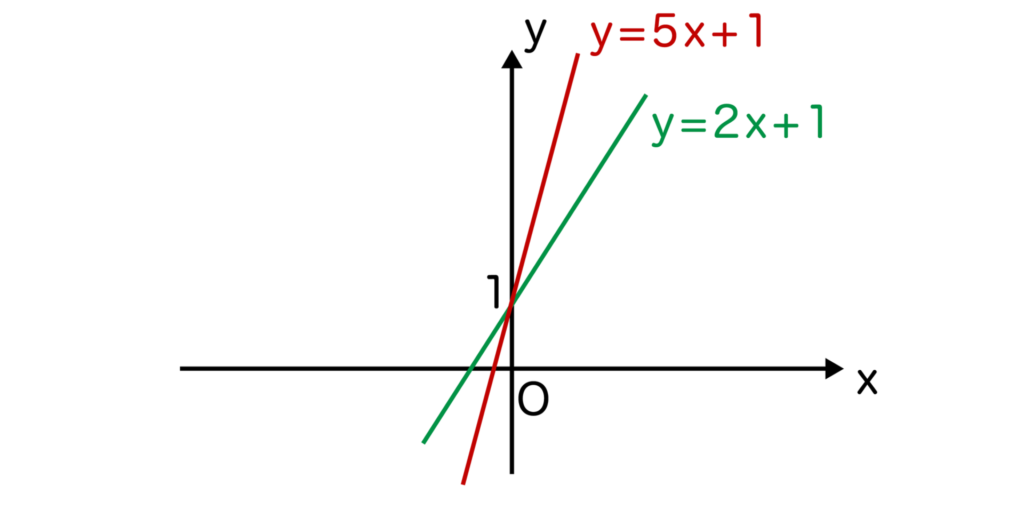
変化の割合がマイナスの場合はでも考え方は同じです。
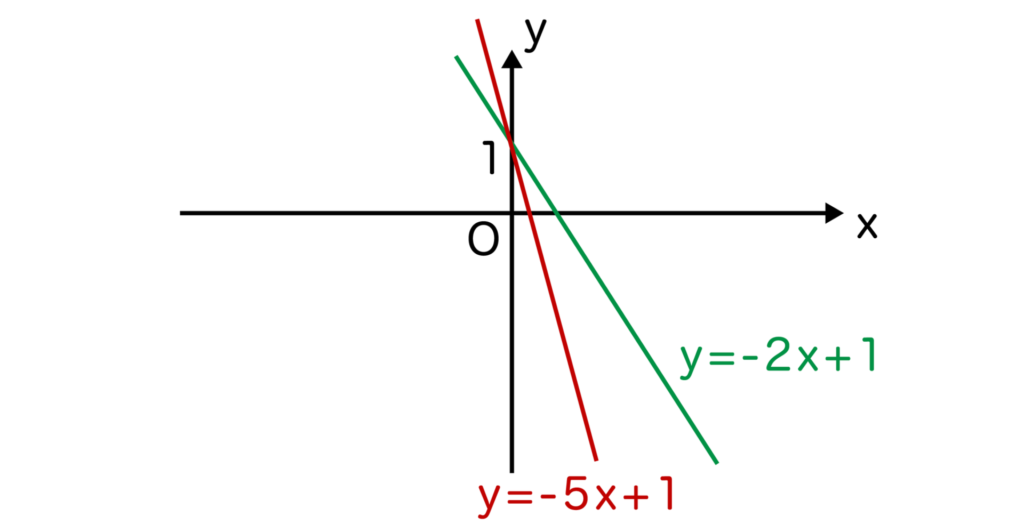
y=-2x+1とy=-5x+1と比較してみます。
y=-2x+1は変化の割合(傾き)の絶対値=2で、y=-5x+1は変化の割合(傾き)の絶対値=5なので、以下の図のようにy=-5x+1の方がグラフが急になります。
一次関数のグラフを書くときに使える知識なので、ぜひ知っておきましょう。
一次関数の変化の割合・傾きに関する問題
最後に一次関数の変化の割合・傾きに関する問題をご紹介します。
すべて基本問題なので、全問正解できるようにしておきましょう。
【練習問題1】
以下の一次関数における変化の割合を求めよ。
(1)y=4x+20
(2)点(-4,-7)と点(3,14)を通る一次関数
(3)点(-5,35)と点(-2,20)を通る一次関数
【解答&解説】
(1)傾きが4の一次関数なので、変化の割合も4となります。
(2)変化の割合=yの増加量 / xの増加量で求めることができるのでした。
よって、{14-(-7)} / {3-(-4)} = 21/7=3・・・(答)となります。
(3)こちらもyの増加量 / xの増加量で変化の割合を求めましょう。
(20-35)/{-2-(-5)}= -15/3=-5・・・(答)となります。
【練習問題2】
一次関数y=6x-10において、xの値が3から5に変化したときのyの増加量を求めよ。
【解答&解説】
繰り返しにはなりますが、変化の割合=yの増加量 / xの増加量です。
傾きが6なので、変化の割合=6となります。xの値が3から5に変化しているので、xの増加量=5-3=2です。
よって、6=yの増加量 / 2より、yの増加量=12となります。
※実際に検算してみましょう。x=3のとき、y=6×3-10=8です。
x=5のとき、y=6×5-10=20です。確かにyの増加量は20-8=12になっていることがわかります。
いかがでしたでしょうか?
今回は一次関数における変化の割合・傾きについて解説していきました。
変化の割合という概念はこの後に学習する二次関数でも登場します。変化の割合=yの増加量 / xの増加量という公式は必ず覚えておきましょう。
※一次関数では変域(定義域・値域)という重要用語も登場します。一次関数の変域とは何かについて解説した記事もご用意しているので、ぜひ合わせてご覧ください。