二次不等式の解5パターンをグラフとともに丁寧に解説！

二次不等式の解にはさまざまなパターンがあり、1つ1つの内容をしっかりと理解することが重要です。

特に、二次不等式では解＝「すべての実数」や「解なし」となる場合もあるので注意が必要です。

そこで今回は早稲田大学教育学部数学科を卒業した筆者が二次不等式の解5パターンについてグラフとともにわかりやすく解説していきます。

※二次不等式の解き方について解説した記事もぜひ参考にしてください。

二次不等式の解：パターン1

a>0かつ判別式D>0のとき、二次方程式ax²+bx+c=0の異なる2つの解をα、β（α<β）とします。

※判別式がわからない人は判別式とは何かについて解説した記事をご覧ください。

すると、

• ax²+bx+c>0の解は、x<α、β<x
• ax²+bx+c<0の解は、α<x<β

となります。上記が成り立つ理由ですが、y=ax²+bx+cのグラフを考えてみると、a>0かつD>0よりグラフは以下のようになりますね。

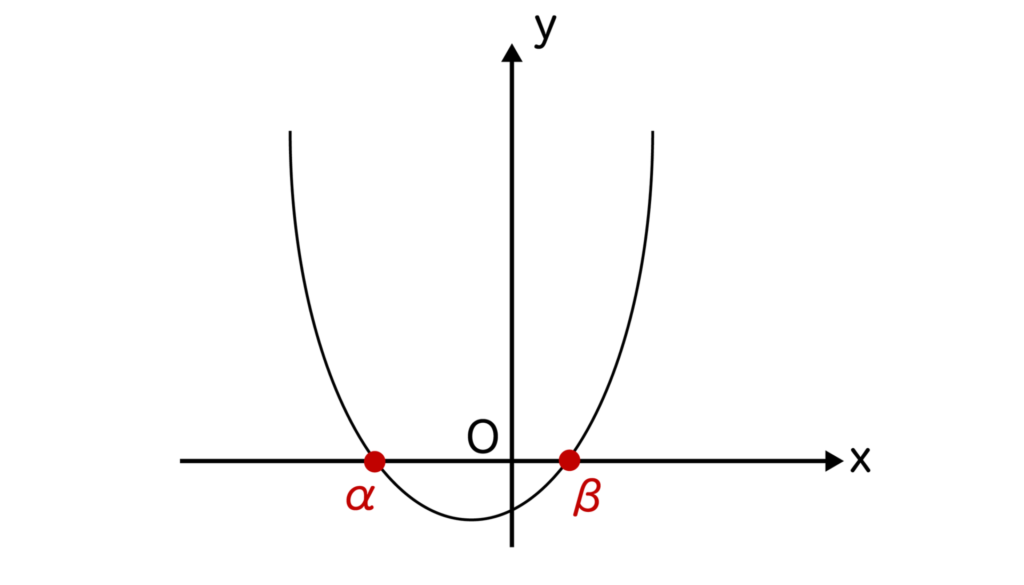
※上記のグラフになる理由がわからない人は二次関数のグラフの作成方法を解説した記事をご覧ください。

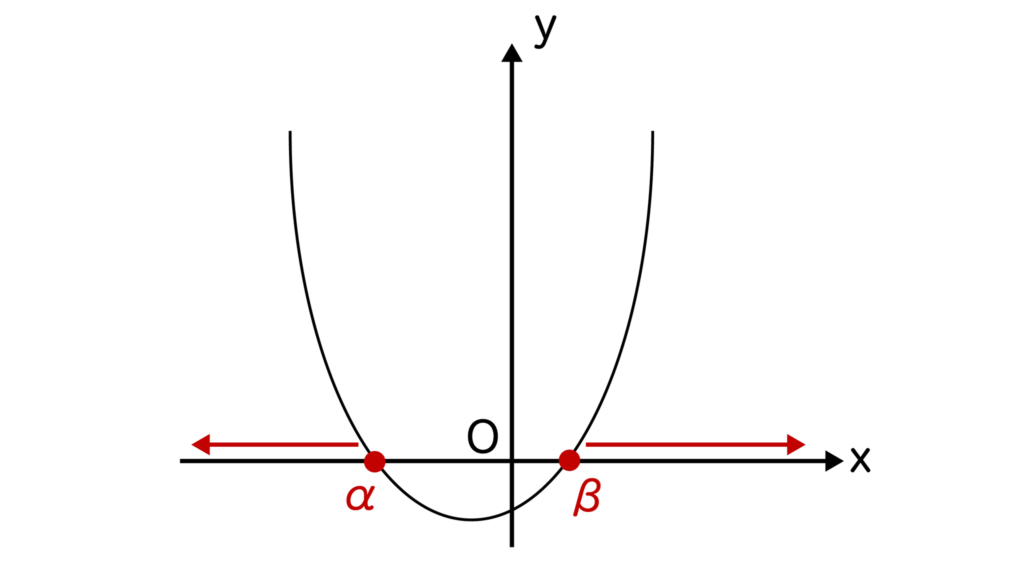
すると、ax²+bx+c>0つまり、y>0の箇所はx<α、β<xであることがわかります。

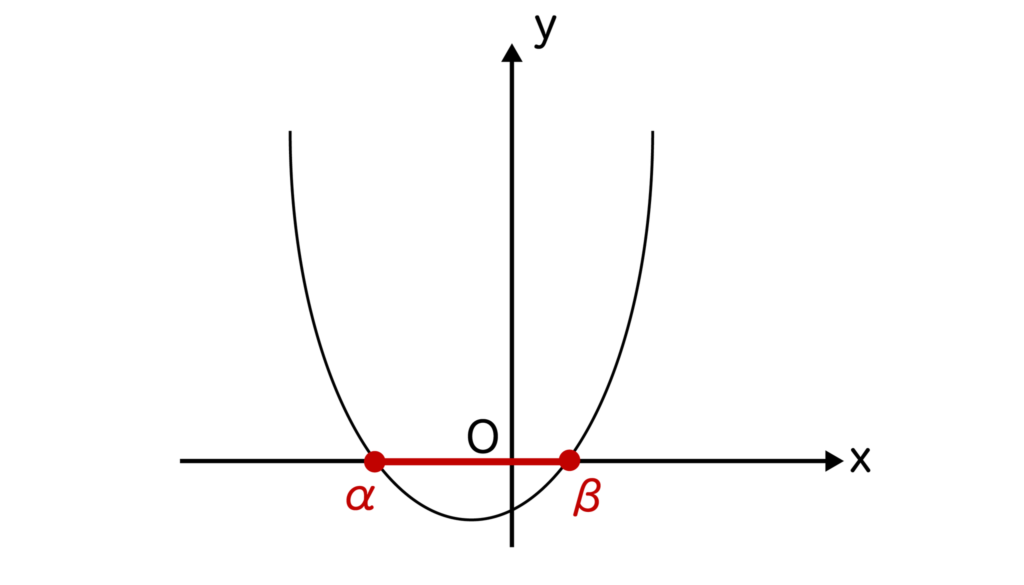
ax²+bx+c<0つまり、y<0の箇所はα<x<βであることがわかります。

ちなみに、「>」や「<」が「≧」や「≦」になった場合も中身は同じです。つまり

• ax²+bx+c≧0の解は、x≦α、β≦x
• ax²+bx+c≦0の解は、α≦x≦β

となります。合わせて覚えておきましょう。

※記号「>」「<」や「≧」「≦」の意味がわからない人は不等号の意味や読み方について解説した記事をご覧ください。

二次不等式の解：パターン2

a>0かつ判別式D>0のとき、二次方程式ax²+bx+c=0の異なる2つの解をα、β（α<β）とします。

すると、

• （x-α）（x-β）>0の解は、x<α、β<x
• （x-α）（x-β）<0の解は、α<x<β

となります。

以上が成り立つ理由ですが、パターン1の冒頭で解説した通り、a>0かつ判別式D>0のとき、二次方程式ax²+bx+c=0の異なる2つの解をα、β（α<β）としているので、ax²+bx+c＝（x-α）（x-β）に因数分解できるためです。

※因数分解がわからない人は数学1の因数分解について解説した記事をご覧ください。

こちらに関しても「>」や「<」が「≧」や「≦」になった場合も中身は同じです。つまり

• （x-α）（x-β）≧0の解は、x≦α、β≦x
• （x-α）（x-β）≦0の解は、α≦x≦β

が成り立ちます。

二次不等式の解：パターン3

a>0かつ判別式D=0のとき、二次方程式ax²+bx+c=0の重解をαとします。

すると、

• ax²+bx+c>0の解は、α以外のすべての実数
• ax²+bx+c<0の解はなし

が成り立ちます。

上記が成り立つ理由をグラフで考えてみます。二次関数y=ax²+bx+cを考えてみましょう。

a>0かつ判別式D=0、二次方程式ax²+bx+c=0の重解をαとすると、グラフは以下のようになりますね。

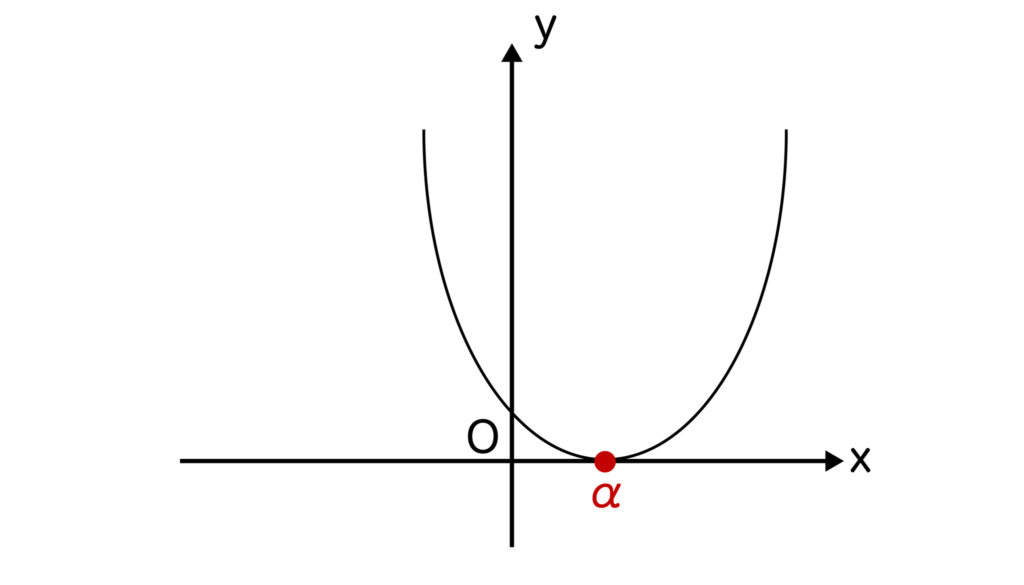
よって、ax²+bx+c>0つまりy>0の解はα以外のすべての実数であることがわかります。

※実数が何かわからない人は、実数とは何かについて解説した記事をご覧ください。

また、ax²+bx+c<0つまりy<0になっているところはグラフ上にどこにもないので解なしとなります。

では、

• ax²+bx+c≧0の解
• ax²+bx+c≦0の解

はどうなるでしょうか？

上記のグラフより、ax²+bx+c≧0つまりy≧0はx=αのときも成り立っているので、解はすべての実数となります。

そして、ax²+bx+c≦0つまりy≦0はx=αのときのみ成り立っているので、解はx=αとなります。

まとめると、

• ax²+bx+c≧0の解は、すべての実数
• ax²+bx+c≦0の解は、x=α

となります。パターン1・2のときとは違って「>」や「<」が「≧」や「≦」になった場合は解がガラリと変わるのでご注意ください。

※二次不等式で解が全ての実数となるケースについて詳しく解説した記事もぜひ参考にしてください。

二次不等式の解：パターン4

a>0かつ判別式D=0のとき、二次方程式ax²+bx+c=0の重解をαとします。

すると、

• （x-α）²>0の解は、α以外のすべての実数
• （x-α）²<0の解はなし

となります。上記が成り立つ理由ですが、ax²+bx+c=0の重解がαなので、ax²+bx+c＝（x-α）²に因数分解できますね。

パターン3で解説した通り、

• ax²+bx+c>0の解は、α以外のすべての実数
• ax²+bx+c<0の解はなし

なので、ax²+bx+cを（x-α）²に置き換えているだけです。

よって、

• ax²+bx+c≧0の解は、すべての実数
• ax²+bx+c≦0の解は、x=α

に関してもax²+bx+cを（x-α）²に置き換えて、

• （x-α）²≧0の解は、すべての実数
• （x-α）²≦0の解は、x=α

が成り立ちます。

二次不等式の解：パターン5

いよいよ最後のパターンとなります。

a>0かつ判別式D<0のとき、

• ax²+bx+c>0の解は、すべての実数
• ax²+bx+c<0の解はなし

が成り立ちます。

こちらもグラフで考えていきます。y=ax²+bx+cとすると、a>0かつD<0よりグラフは以下のようになります。x軸と接するところは1つもありません。

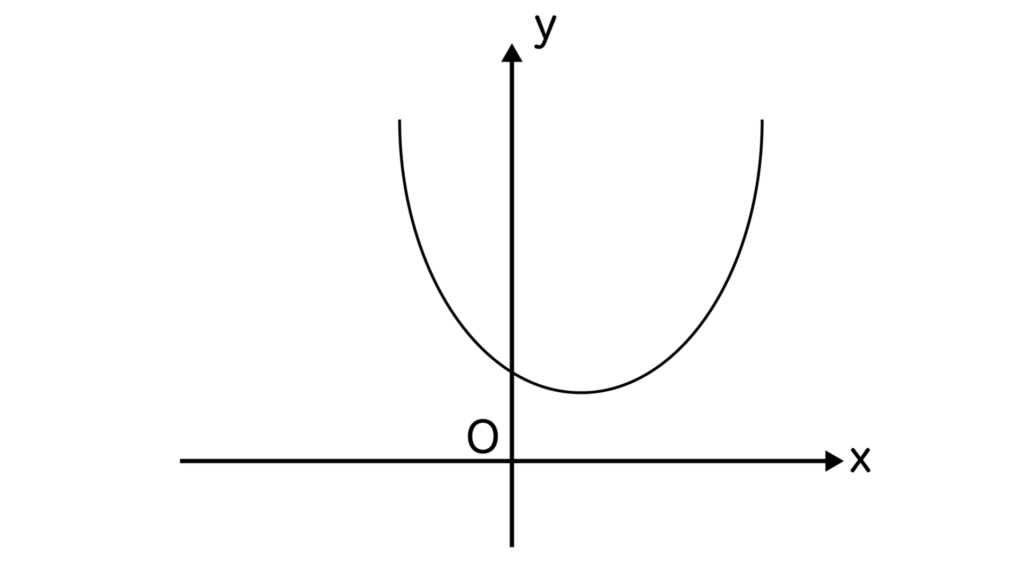
ax²+bx+c>0つまり、y>0になっている部分はグラフの全部なので、解はすべての実数となります。

そして、ax²+bx+c<0つまり、y<0になっている部分はグラフに1つもないので解なしとなります。

では、「>」や「<」が「≧」や「≦」になった場合はどうでしょうか？

ax²+bx+c≧0つまり、y≧0を考えてみるとグラフはすべてy≧0になっているので「ax²+bx+c>0」のときと変わらず解はすべての実数となります。

ax²+bx+c≦0に関しても同様です。グラフでy≦0になっている箇所は1つもないので「ax²+bx+c<0」のときと変わらず解なしとなります。

まとめると、

• ax²+bx+c≧0の解は、すべての実数
• ax²+bx+c≦0の解はなし

となります。

※二次不等式で解なしとなるケースについて詳しく解説した記事もご用意しているので、ぜひ参考にしてください。

二次不等式の解を求める計算問題

では、上記を踏まえて二次不等式の解を求める計算問題を解いてみましょう。

【問題】

以下の二次不等式を解きなさい。

（1）x²+x-2>0

（2）x²-4x+2≧0

（3）2x²-4x-48<0

（4）x²+x+2<0

（5）x²-10x+25>0

【解答＆解説】

（1）x²+x-2=0を解くきます。

（x-1）（x+2）=0より、x=1、-2となるのでx<-2、1<x・・・（答）となります。

（2）x²-4x+2=0を解きます。解の公式より、x=2±√2となります。

※解の公式がわからない人は二次方程式の解の公式とは何かについて解説した記事をご覧ください。

よってx≦2-√2、2+√2≦x・・・（答）となります。

（3）2x²-4x-48=0を解くとx=-4、6となるので、-4<x<6・・・（答）となります。

（4）x²+x+2=0の判別式をDとすると、

D=1²-4×1×2=-7<0となるので、解はない・・・（答）

（5）x²-10x+25＝（x-5）²より、解は5以外のすべての実数・・・（答）

いかがでしたか？今回は二次不等式の解5パターンをグラフとともに解説していきました。

今回ご紹介した事項は公式として暗記してしまいましょう。二次不等式の計算問題を解くためには必ず覚えておかなければならない知識となります。