二次関数の変化の割合の公式！傾き・切片も秒でわかる！

変化の割合は一次関数の分野でも登場しましたが、二次関数でも変化の割合は存在します。

今回は早稲田大学教育学部数学科を卒業した筆者が二次関数における変化の割合の公式や傾き、切片について解説します。

数学が苦手な人でも理解できるよう図解を使いながら解説しているので、ぜひ最後までお読みください。

二次関数における変化の割合の公式

まずは二次関数における変化の割合の公式から解説します。

一次関数の変化の割合の公式について解説した記事の通り、変化の割合＝yの増加量/xの増加量で求めることができます。これは一次関数だろうが二次関数だろうが変わりません。

以上が変化の割合の公式となります。必ず覚えておきましょう。

では、例題を1つ解いてみます。

【例題】

二次関数y＝x²+5x+3において、xの値が4から7に変化したときの変化の割合を求めよ。

【解答＆解説】

xの値が4から7に変化しているので、xの増加量＝7-4＝3ですね。

x＝4のとき、y＝4²+5×4+3＝39です。

x＝7のとき、y＝7²+5×7+3＝87です。

よって、yの増加量＝87-39＝48となります。

以上より、変化の割合＝48/3＝16・・・（答）となります。

二次関数の変化の割合は一目ではわからない

一次関数においては変化の割合＝傾きでしたので、例えばy＝5x-2という一次関数があったとき、変化の割合＝傾き＝5と一目でわかりましたが、二次関数における変化の割合は一目ではわかりません。

必ず変化の割合の公式であるyの増加量/xの増加量を使って計算しなければならないのでご注意ください。

また、一時関数における変化の割合は傾きと同じなので常に一定ですが、二次関数においてはxの増加量やyの増加量によって変化の割合は変化します。

例えば、上記の例題の通り二次関数y＝x²+5x+3において、xの値が4から7に変化したときの変化の割合は16でしたが、xの値が2から10に変化したときの変化の割合はどうでしょうか？

xが2から10に変化しているので、xの増加量＝8ですね。

x=2のときy=17、x=10のときy=153なので、yの増加量＝153-17=136となります。

よって変化の割合＝136/8=17となり、先ほどの16とは異なる値となりました。

二次関数の変化の割合は常に一定ではないということもしっかり覚えておきましょう。

二次関数における傾きと切片

では、二次関数における傾きと切片はどうやって求めるのでしょうか？

結論から申しますと、二次関数においては傾きという概念は存在しません。

なので、「二次関数y＝7x²-2x+1の傾きを求めよ」といった問題が出題されることはありません。

二次関数は以下の図のように放物線状のグラフとなり、一次関数のグラフのように直線ではありません。

※二次関数のグラフの作成方法を解説した記事もぜひ合わせてご覧ください。

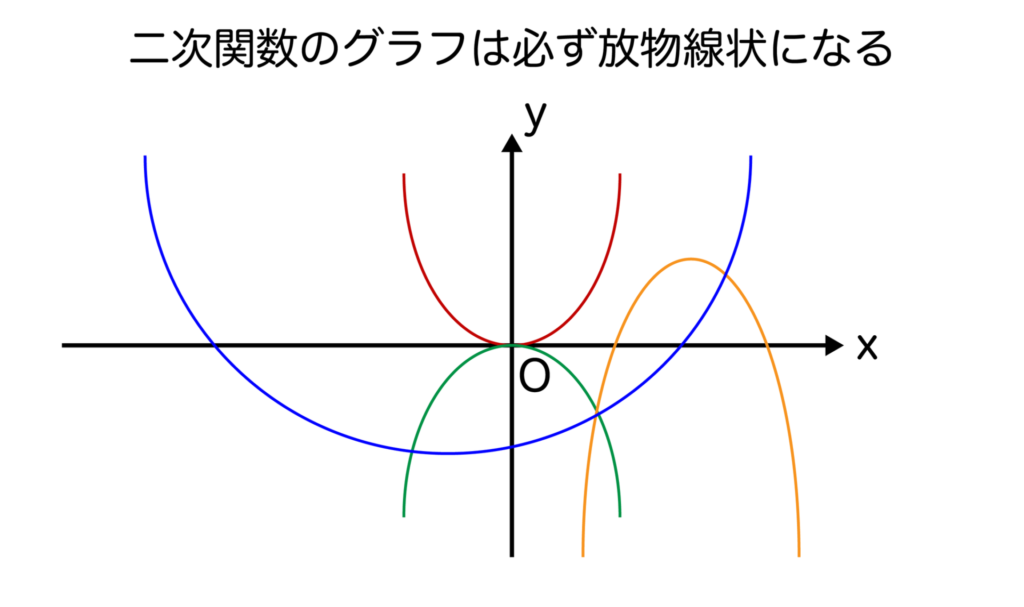
つまり、傾きが一定ではないので二次関数においては傾きという概念がないのです。

では、切片はどうでしょうか？

切片にはx切片とy切片がありますが、x切片はy=0のときのxの値、y切片はx=0のときのyの値となります。

例として、二次関数y=x2+8x+15のx切片とy切片を求めてみましょう。

まずはx切片からです。y=0のとき、

0=x²+8x+15より、0=（x+5）（x+3）となるので、x切片は-3、-5となります。

※因数分解のやり方がわからない人は数学1の因数分解について解説した記事をご覧ください。

次はy切片を求めます。x=0のとき、y=15となるのでy切片は15となります。

二次関数においては定数項の部分がy切片となりますので、覚えておきましょう。

※定数項がわからない人は多項式の定義について解説した記事をご覧ください。

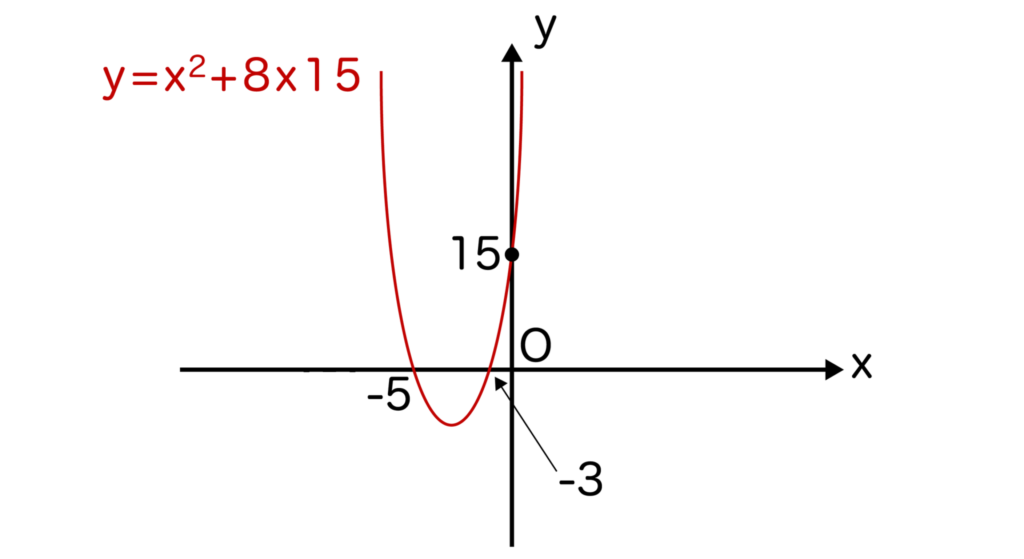
ちなみに、y=x²+8x+15のグラフは以下となります。x切片とy切片の位置を確認しておきましょう。

二次関数の変化の割合・切片の練習問題

最後に二次関数の変化の割合・切片に関する練習問題を用意しました。

全問解けるようになるまでしっかりと上記を理解しましょう。

【練習問題】

（1）二次関数y=3x²+x+1において、xの値が5から9に変化したときの変化の割合を求めよ。

（2）二次関数y=-x²-x+1において、xの値が-2から-10に変化したときの変化の割合を求めよ。

（3）二次関数y=-2x²-11x-5におけるx切片とy切片を求めよ。

【解答＆解説】

（1）x=5のときy=3×52+5+1=81、x=9のときy=3×92+9+1=343

よって、yの増加量は343-81=262

xの増加量は9-5=4なので、変化の割合＝262/4=131/2・・・（答）

（2）（1）と同様に考えて、x=-2のときy=-3、x=-10のときy=-89

xの増加量は-10-(-2)=-8なので、変化の割合＝ -89 / -8 =89/8・・・（答）

（3）x切片はy=0のときのxの値のことでした。

0=-2x²-11x-5より、0=-（2x+1）（x+5）となるので、x=-1/2、-5・・・（答）となります。

y切片はx=0のときのyの値のことであり、二次関数の式の定数項なので-5・・・（答）となります。

今回は二次関数の変化の割合の公式・傾き・切片について解説していきました。

本記事で解説したことはすべて二次関数の基本的な事柄なので、必ず理解しておきましょう！