二次方程式を利用した応用問題や文章題は大学入試でも頻出なので対策は必須です。
本記事では早稲田大学教育学部数学科を卒業した筆者が二次方程式を利用した応用問題・文章題を解く流れについて解説した後、二次方程式を利用した応用問題・文章題を5問ご紹介します。
数学が苦手な人でも理解できるように詳しい解答&解説も付けているので、ぜひチャレンジしてみてください。
※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式を利用した応用問題・文章題の解き方
まずは二次方程式を利用した応用問題・文章題の解き方の流れについて解説します。
基本的には未知数をxやaなどの文字に置き換えて二次方程式を立てるのですが、そのときのポイントは求める未知数をxやaなどの文字にすることです。
例えば、文章題で「A君が持っていた金額を求めよ」という問題が用意されているのであれば、A君が持っていた金額をx[円]とおけば良いのです。
もちろんすべての問題において求める未知数をxやaなどの文字にすればOKというわけではありませんが、基本的には求める未知数をxやaなどの文字にした方が問題を解きやすいケースが多いです。
そして、未知数を文字にしたら問題文の情報から二次方程式を立てて、その二次方程式を解けば良いです。
※二次方程式の解き方について解説した記事もぜひ合わせてご覧ください。
以上が二次方程式を利用した応用問題・文章題の解き方の流れとなります。
二次方程式を利用した応用問題・文章題その1
方程式(a2-4)x2+2ax+1=0の実数解の個数を求めよ。
【解答&解説】
問題が「二次方程式」ではなく単に「方程式」となっていることに注意しましょう。
二次方程式である必要はありません。
つまり、a=±2のときとそうでないときで場合分けが必要となります(a=±2のときは一次方程式になりますね)
※一次方程式の解き方について解説した記事もご用意しているので、忘れてしまった人はぜひ参考にしてください。
[1]a=±2のとき
方程式は±4x+1=0となり、a=2、a=-2それぞれについて方程式は実数解を1個持ちます。
[2]a≠±2のとき
方程式は二次方程式となり、判別式をD/4とするとD/4=a2-(a2-4)×1=4>0となるので異なる2つの実数解を持ちます。
※二次方程式の実数解の個数は判別式を利用すればわかるのでした。判別式について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式を利用した応用問題・文章題その2
aを定数とするとき、方程式ax+2=x+a2を解きなさい。
【解答&解説】
ax+2=x+a2より、(a-1)x=a2-2・・・①となりますね。
[1]a-1=0、すなわちa=1のとき
①は0 × x=-1となり、これを満たすxは存在しません。よって解なしとなります。
[2]a-1≠0、すなわちa≠1のとき
①よりx=(a2-2)/(a-1)となります。
二次方程式を利用した応用問題・文章題その3
2つの二次方程式x2+6x+12k-24=0とx2+(k+3)x+12=0がただ1つの実数を共有解として持つとき、実数の定数kの値を求めよ。また、そのときの共通解も求めよ。
【解答&解説】
2つの二次方程式の共通解をαとおいてみましょう。
すると、
- α2+6α+12k-24=0・・・①
- α2+(k+3)α+12=0・・・②
という連立方程式が立てられるので、
②-①より、(k-3)α-12k+36=0となるので、(k-3)(α-12)=0となります。
したがって、k=3、α=12となります。
二次方程式を利用した応用問題・文章題その4
二次関数y=ax2+bx+cが点(-1、0)と(3、8)を通り、一次関数y=2x+6に接するとき、a、b、cの値を求めよ。
【解答&解説】
y=ax2+bx+cが点(-1、0)と(3、8)を通るので、
- 0=a-b+c・・・①
- 8=9a+3b+c・・・②
となりますね。
②-①より、8a+4b=8となるので、b=-2a+2・・・③となります。
③を①に代入して、0=a-(-2a+2)+cより、
c=-3a+2・・・④が導けます。
③と④をy=ax2+bx+cに代入すると、
y=ax2+(-2a+2)x-3a+2となり、bとcを消去することができました。
これと一次関数y=2x+6からyを消去すると、
ax2+(-2a+2)x-3a+2=2x+6となり、整理すると、
ax2-2ax-3a-4=0となります。
判別式をD/4とすると、D/4=a2-a(-3a-4)=4a2+4a=4a(a+1)となりますね。
二次関数ax2+(-2a+2)x-3a+2が一次関数y=2x+6に接するための条件はD=0なので、a=-1、0となります。
ここで、y=ax2+bx+cは二次関数であることからa=0は不適となるので、a=-1となります。
a=-1を③と④に代入して、b=4、c=5となります。
二次方程式を利用した応用問題・文章題その5
以下の図のような正方形ABCDの紙を用意し、この紙の四隅から1辺の長さが2cmの正方形を4つ切り取って体積が450cm3の直方体を作りたい。このとき、ABの長さは何cmにすればよいか求めなさい。
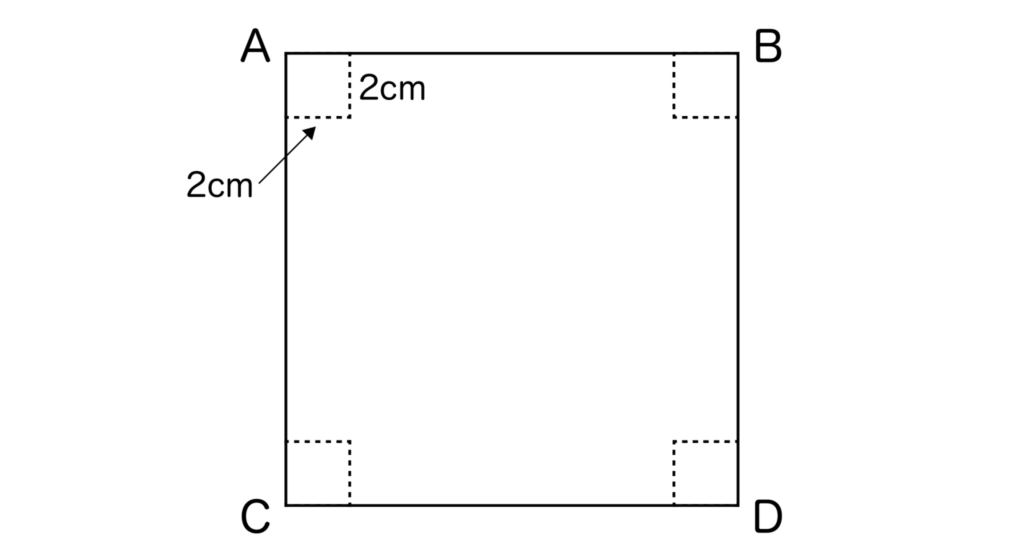
【解答&解説】
ABの長さを求めたいので、AB=x[cm]とおきましょう。また、直方体の体積=底面積×高さでしたね。
以下の図のように底面積をEFGHとみなすと、高さは2cmとなります。
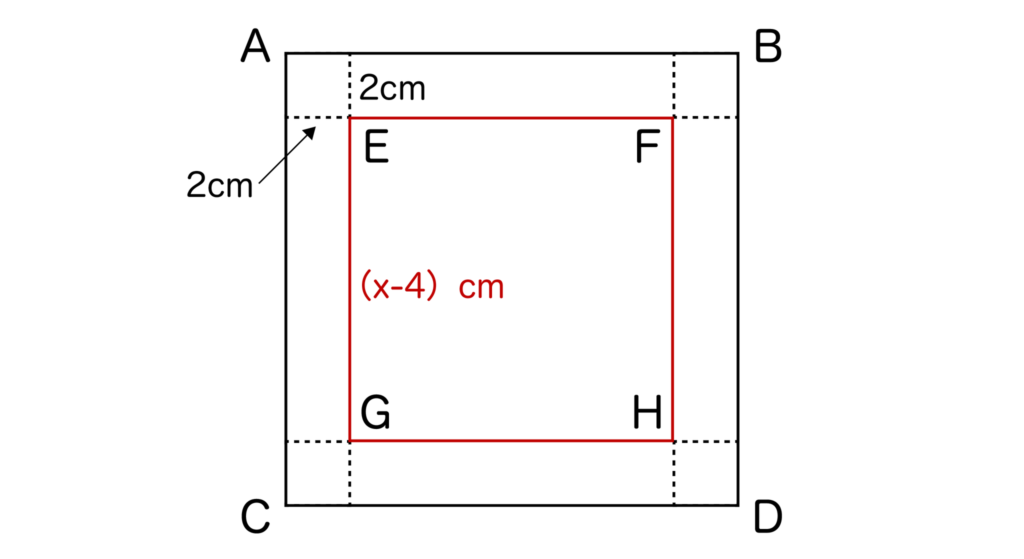
底面積EFGHは正方形でありEF=x-4[cm]なので、底面積=(x-4)2[cm2]となりますね。
よって、(x-4)2×2=450より、(x-4)2=225となり、x-4=±15となります。
※x-4=±15になる理由がわからない人は平方根とは何かについて解説した記事をご覧ください。
よってx=19、-11となりますが、xはABの長さで正の値になるのでx=-11は不適となります。
よって、x=19[cm]となります。
いかがでしたでしょうか?二次方程式を利用した応用問題・文章題を5問ご紹介しました。
問題文で単に「方程式」と言われた場合は二次方程式以外の可能性も考慮することを忘れないようにしましょう。これからもたくさんの応用問題を解いていき、大学入試や共通テストに備えてください。


