二次関数の式を求める場合、頂点の座標とその二次関数が通るもう1点の座標が分かれば二次関数の式は求めることができますが、頂点がわからない場合は基本的に3点の情報が必要となります。
※頂点から二次関数の式を求める方法については二次関数の頂点とは何かについて解説した記事をご覧ください。
そこで本記事では早稲田大学教育学部数学科を卒業した筆者が3点を通る二次関数の求め方について解説していきます。
裏ワザも2つご紹介しているので、ぜひ最後までお読みください。
3点を通る二次関数の求め方(王道編)
3点を通る二次関数の求め方の王道パターンは連立方程式を活用することです。
例題を使いながら解説していきます。
【例題】
3点(2、19)(1、8)(3、34)を通る二次関数の式を求めよ。
【解答&解説】
求める二次関数の式をy=ax2+bx+cとおきます。
すると、問題文の条件より
- 19=4a+2b+c・・・①
- 8=a+b+c・・・②
- 34=9a+3b+c・・・③
が成り立ちますね。
cの係数がすべて1なので、cを消すことを考えましょう。
※係数がわからない人は多項式の定義について解説した記事をご覧ください。
①-②より、11=3a+b・・・④です。
③-②より、26=8a+2b、つまり13=4a+b・・・⑤です。
⑤-④より、a=2が導けます。これを④に代入してb=5が導けます。
a=2、b=5を②に代入して、c=1となります。
よって求める二次方程式の式はy=2x2+5x+1となります。
以上が王道的な3点を通る二次関数の求め方です。この求め方は必ず理解しておきましょう。
上記のように、3点を通る二次関数の式を求める際にはy=ax2+bx+cの定数項であるcを消すことを意識しながら連立方程式を解くと良いです。
3点を通る二次関数の求め方(裏ワザ編)
先ほどは連立方程式を利用した王道的な3点を通る二次関数の求め方を解説しましたが、ここからは3点を通る二次関数の求め方として裏ワザを2つご紹介します。
裏ワザその1
こちらも例題で解説していきます。
【例題】
3点(-3、0)(1、0)(2、-10)を通る二次関数の式を求めよ。
【解答&解説】
今回は(-3、0)と(1、0)がともにy=0であることに注目します。
(p、0)(q、0)を通る二次関数の式はy=a(x-p)(x-q)で表すことができます。
※x=pを代入するとy=0、x=qを代入するとy=0になることが確認できます。
よって、今回求める二次関数はy=a(x+3)(x-1)とおくことができます。
これに(2、-10)を代入すると、
-10=a×5×1よりa=-2となります。
よって答えはy=-2(x+3)(x-1)となるので、y=-2x2-4x+6・・・(答)となります。
※この裏ワザは3点のうち2点のyが0である場合のみ使えるワザとなりますのでご注意ください。
裏ワザその2
裏ワザ2つ目のご紹介です。こちらも例題で解説します。
【例題】
3点(1、1)(2、3)(3、9)を通る二次関数の式を求めよ。
【解答&解説】
今回は先ほどのように3点のうち2点のyが0でなくても使える裏ワザとなります。
まずは3点のうち2点を選び、その2点を通る一次関数の式を導きます。
※一次関数がわからない人は一次関数とは何かについて解説した記事をご覧ください。
今回は点(1、1)と(2、3)を通る一次関数の式を考えてみましょう。
傾き=(3-1)/(2-1)=2となるので、y=2x+bに(1、1)を代入して1=2+bより、b=-1となるので、y=2x-1が導けます。
※傾きの求め方がわからない人は一次関数の変化の割合・傾きの求め方について解説した記事をご覧ください。
すると、求める二次関数の式はy=a(x-1)(x-2)+(2x-1)・・・①と表すことができます(細かい証明は本記事では割愛させていただきます)

この二次関数が(3、9)を通るので、
9=a×2×1+(6-1)=2a+5より、a=2が導けます。
①にa=2を代入すると、y=2(x2-3x+2)+(2x-1)より求める二次関数の式はy=2x2-4x+3となります。
※展開のやり方・整理方法がわからない人は多項式の計算について解説した記事をご覧ください。
この裏ワザは連立方程式を解くのがめんどくさそうなときにぜひお使いください。
3点を通る二次関数の求める練習問題
最後に3点を通る二次関数の求める練習問題をご用意しました。
全問正解できるまで繰り返し解きましょう。
【練習問題】
以下の3点を通る二次関数を求めよ。
(1)点(1、6)(2、12)(4、30)
(2)点(4、68)(2、22)(3、42)
【解答&解説】
(1)求める二次関数の式をy=ax2+bx+cとおきましょう。
- 6=a+b+c・・・①
- 12=4a+2b+c・・・②
- 30=16a+4b+c・・・③
より、cを消すことを考えます。
②-①より6=3a+b・・・④
③-②より18=12a+2b・・・⑤
⑤-2×④より6=6aとなるのでa=1が求まります。
a=1を④に代入してb=3が求まります。
a=1、b=3を①に代入してc=2が求まります。
よって求める二次関数の式はy=x2+3x+2・・・(答)となります。
(2)せっかくなので、上記でご紹介した裏ワザ2を使って解いてみましょう。
点(4、68)と(2、22)を通る直線(一次関数)の式はy=23x-24ですね。
すると、求める二次関数の式はy=a(x-4)(x-2)+(23x-24)・・・①と表すこことができます。
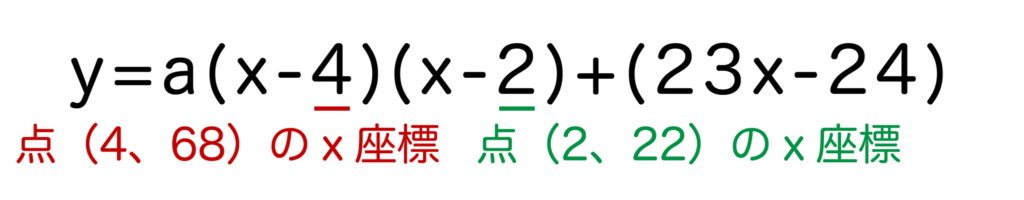
①に残りの点(3、42)を代入すると、
42=a×(-1)×1+(23×3-24)=-a+45となるのでa=3となります。
a=3を①に代入して、y=3(x2-6x+8)+(23x-24)=3x2+5x・・・(答)となります。
いかがでしたでしょうか?
今回は3点を通る二次関数の求め方について解説しました。基本的には連立方程式を使った求め方さえ覚えておけば問題ありあません。
余力がある人は裏ワザ2の方法も覚えておきましょう。


