今回は高校数学の数学1で登場する一次不等式を取り上げます。
一次不等式は共通テストで頻出の分野の1つなので、必ず解けるようにしておきましょう。
本記事では、早稲田大学教育学部数学科を卒業した筆者が一次不等式とはどんな式なのかについて解説した後、一次不等式の解き方や絶対値がある場合の解き方だけでなく、整数解を求める問題や応用問題・文書題などもご紹介していきます。
数学が苦手な高校生でも理解できるようにわかりやすい解説をこころがけているので、ぜひ最後までお読みください。
一次不等式とは?不等式の性質も
一次不等式とは何かを理解し、問題を解くためには不等号の意味や不等式の性質を理解しておかなければなりません。
※不等号の意味や読み方について解説した記事もぜひ合わせてご覧ください。
なので、まずは不等式の性質から解説していきます。以下4つの性質は必ず覚えましょう。
- a<b、b<cならば、a<c
- a<bならば、a+c<b+c、a-c<b-c
- a<b、c>0ならばac<bc、a/c < b/c
- a<b、c<0ならばac>bc、a/c > b/c
特に注意すべきは4です。負の数(=c)をかけたり、負の数で割ったりすると不等号の向きが変わるのでご注意ください。
例えば、a=10、b=20、c=-2とします。このとき、a<bが成立しており、両辺に-2をかけると、
10×(-2)>20×(-2)
=-20>-40
となります。また、両辺を(-2)で割ると、
10/(-2)>20/(-2)
=-5>-10
となります。
そして、一次不等式とは何かについてですが、不等式のすべての項を左辺に移行して整理したとき、ax+b>0、ax+b≦0のように、左辺がxの一次式になる不等式を「xについての一次不等式」と言います。ただし、a、bは定数でaは0ではないものとします。
※一次式とは何かについて解説した記事もぜひ参考にしてください。
※「項」が何かわからない人は多項式の定義について解説した記事をご覧ください。
一次不等式の解き方
言葉だけだとイメージがつかないと思いますので、例題で解き方を解説していきます。
一次不等式を6x-10<3xを解いてみましょう。
一次不等式の解き方としてはxを左辺に寄せ、定数項を右辺に寄せるのが定石です。
6x-10<3x=6x-3x<10=3x<10となります。
そして、両辺を3で割ります。先ほどご紹介した不等式の性質より、x<10/3・・・(答)となります。3は正の数なので、不等号の向きは変わらないことにご注意ください。
x>〇〇や、x≦〇〇のような形にすることがゴールとなります。
一次不等式に分数がある場合
一次不等式に分数がある場合は、両辺に数をかけて一次不等式を整理します。
例題をご紹介します。
(5x+1)/4 + 7/3 > x+1を解いてみましょう。
分母が4と3なので、4と3の最小公倍数である12を両辺にかけます。12は正の数なので、不等号の向きは変わりません。
(5x+1)/4 + 7/3 > x+1
=3(5x+1)+28 > 12x+12
=15x+31 > 12x+12
=3x > -19
=x > -19/3・・・(答)
となります。
一次不等式と数直線
ここからは、一次不等式と数直線の関係について解説していきます。
例えば、とある一次不等式を解いた結果、答えがx<10となったとします。
このとき、xは10よりも小さい数すべて(=無限に存在する)が対象となります。
これは数直線を用いて以下のように表現することができます。
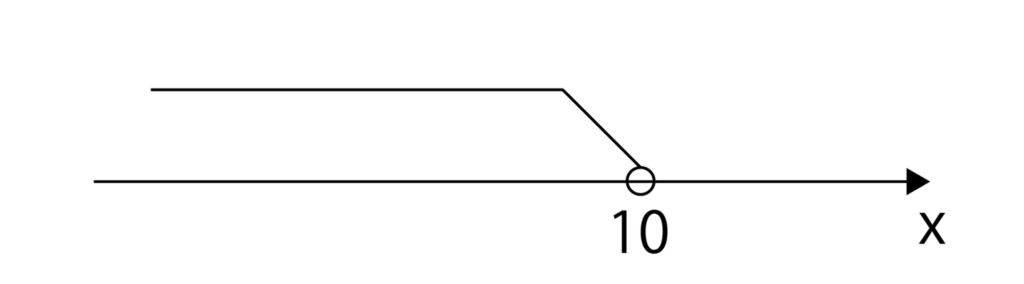
数直線上では、<と≦、>と≧を区別するために、●と◯を利用します。
●は●の点が範囲に含まれることを示し、◯は◯の点が範囲に含まれないことを示しています。
なので、上記のx<10は◯が使用されています。
では、x≧5は数直線上でどう表現できるでしょうか?≧なので、◯ではなく●が使用され、以下のようになります。
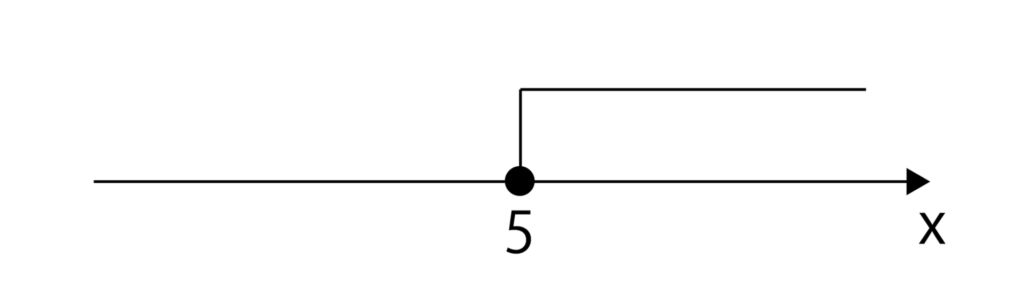
●の場合は線がまっすぐ上に伸びます。◯の場合は線が斜めに伸びます。
一次不等式の結果を数直線上で表現するテクニックは大学入試や共通テストでもよく使いますので、必ずやり方を覚えておきましょう。
連立一次不等式
複数の一次不等式を組み合わせたものを連立一次不等式と言います。
それらの一次不等式を同時に満たすxの値の範囲を求めることを、その連立一次不等式を解くと言います。
例えば、連立一次不等式
- 5x+1≦8x+16
- 2x-3<-x+6
を解いてみましょう。
まずは5x+1≦8x+16を普通に解きます。
5x+1≦8x+16
=-3x≦15
=x≧-5・・・①
となります。
2x-3<-x+6も普通に解きます。
2x-3<-x+6
=3x<9
=x<3・・・②
となります。そして、①と②を同時に満たすxの範囲を考えます。
以下のように数直線で考えるとわかりやすいです。
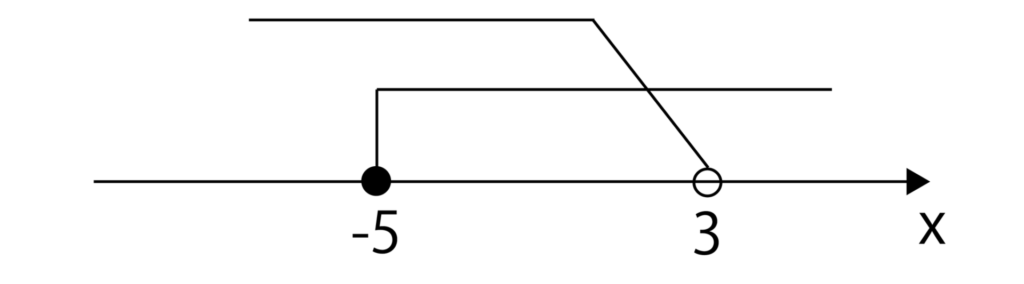
重なっている部分を考えて-5≦x<3・・・(答)となります。
もう1つ例題をご紹介します。
連立一次不等式 -2x+1<3x+4<6x-8を解いてみましょう。
このように、一次不等式が一直線に並んでいる場合は、
- -2x+1<3x+4
- 3x+4<6x-8
の2つにわけて考えます。
-2x+1<3x+4=-5x<3より、x>-3/5・・・③
3x+4<6x-8=-3x<-12より、x>4・・・④
③と④を数直線に表すと以下のようになります。
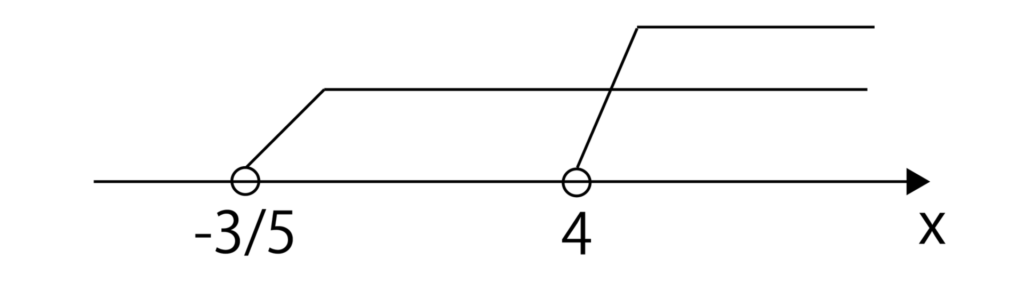
よって、答えはx>4・・・(答)となります。
絶対値を含む一次不等式の解き方
一次不等式に絶対値が含まれているケースがあります。
絶対値を含む一次不等式を解くためには、まずは以下の公式を覚えましょう。
c>0のとき、
- 方程式|x|=cの解は、x=±c
- 不等式|x|<cの解は、-c<xc
- 不等式|x|>cの解は、x<-c、c<x
例えば、一次不等式|x-2|<3を解いてみましょう。
上記より、|x-2|<3=-3<x-2<3より、-1<x<5・・・(答)となります。
一次不等式と整数解
一次不等式に関する問題では「整数解を求めよ」という問題が出題されるケースがあります。
共通テストでもたまに出題される重要問題なので、必ず解き方を覚えておきましょう。
整数解とはその名の通り、解が整数であるもののことです。
例題を1つご紹介します。
一次不等式3x<5x−2<x+12を満たす整数解xをすべて求めてみましょう。
3x<5x−2=-2x<-2より、x>1・・・①
5x−2<x+12=4x<14より、x<7/2・・・②
①・②より、1<x<7/2となります。
7/2=3.5なので、整数解x=2、3・・・(答)となります。
一次不等式の練習問題
ここからは、一次不等式の練習問題をご紹介します。
すべて基本的な問題なので、全問正解できるようにしておきましょう。
以下の一次不等式を解きなさい。
【練習問題1】
(1)5x-7>3(x+3)
(2)(3x+2)/5<2x-1
(3)0.2x+1<-0.3x-2.5
【解答&解説】
(1)5x-7>3(x+3)
=5x-7>3x+9
=2x>16
=x>8・・・(答)
(2)分母に5があるので、両辺を5倍しましょう。5は正の数なので、不等号の向きは変わりません。
(3x+2)/5<2x-1
=3x+2<10x-5
=-7x<-7
=x>1・・・(答)
(3)両辺を10倍して、小数点を取りましょう。
0.2x+1<-0.3x-2.5
=2x+10<-3x-25
=5x<-35
=x<-7・・・(答)
【練習問題2】
連立一次不等式
- 3(x-4)≦x-3
- 6x-2(x+1)<10
を解きなさい。
【解答&解説】
3(x-4)≦x-3
=3x-12≦x-3
=2x≦9
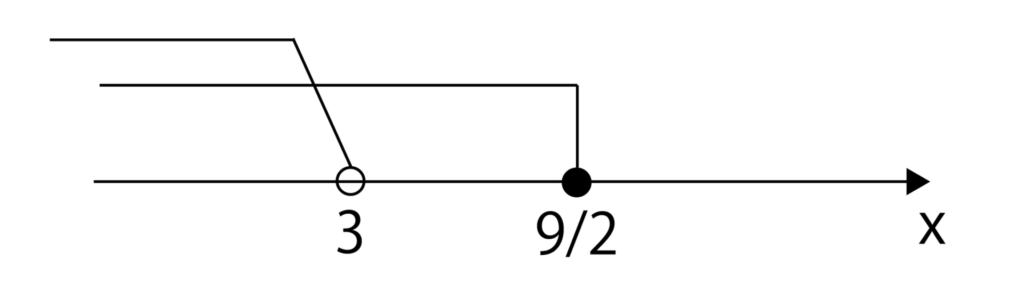
=x≦9/2・・・①
また、6x-2(x+1)<10
=6x-2x-2<10
=4x<12
=x<3・・・②
より、①・②を数直線に表すと以下のようになるので、答えはx<3・・・(答)となります。
【練習問題3】
以下の一次不等式を解きなさい。
|x-5|>3
【解答&解説】
|x-5|>3より、x-5<-3、3<x-5
したがって、x<2、8<x・・・(答)
一次不等式の応用問題と文章題
最後に一次不等式の応用問題と文章題を1つずつご紹介するので、ぜひチャレンジしてみてください。
【応用問題】
一次不等式 ax<-2x+4<2xの解が1<x<4となるとき、aの値を求めなさい。
【解答&解説】
-2x+4<2xより、-4x<-4となるので、x>1です。
よって、解が1<x<4となるためにはax<-2x+4の解がx<4とならなければなりません。
ax<-2x+4
=ax+2x<4
=(a+2)x<4・・・①
より、a>-2のとき、
①=x<4/(a+2)より、a=-1。これはa>-2を満たすので答えとなります。
a=-2のとき、①=0・x<4となり、xはすべての実数となり、x<4となりません。
※実数とは何かについて解説した記事もぜひ参考にしてください。
a<-2のとき、①=x>4/(a+2)より、x<4となることはありません。
よって、答えはa=-1・・・(答)のみとなります。
【文章題】
ある小学校で子どもたちにお菓子を配る。1人に4個ずつ配ると19個余るが、1人に7個ずつ配ると最後の子どもは4個よりも少なくなってしまう。このとき、お菓子は全部で何個あるか求めなさい。
【解答&解説】
子どもの人数をx人とおいてみましょう。
すると、お菓子の個数=4x+19(個)となりますね。
また、1人に7個ずつ配ると、最後の子どもは4個よりも少なくなるので(x-1)人には無事7個ずつ配ることができており、残ったお菓子が最後の子どもの分となるので、
0≦4x+19-7(x-1)<4 という一次不等式を作ることができます。
0≦4x+19-7(x-1)より、
0≦-3×26=x≦26/3・・・①
4x+19-7(x-1)<4
=-3x+26<4
=x>22/3・・・②
①・②より、22/3<x≦26/3となります。
22/3=7.3…で、26/3=8.6…です
xは子どもの数で、自然数であるから=8となります。よって、求めるお菓子の個数は4×8+19=51[個]・・・(答)となります。
今回は一次不等式とはどんな式なのかについて解説した後、一次不等式の解き方や絶対値がある場合の解き方、整数解を求める問題や応用問題などをご紹介していきました。
一次不等式は大学入試や共通テストでも頻出分野の1つなので、しっかりと勉強・対策をしておきましょう。


