皆様はcosθ=0、cosθ=1、cosθ=1/2のときのθの値を自力で求めることができますでしょうか?
これからより深く三角関数の学習をしていくにあたって、自力でθの値を求める能力は必須となります。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がcosθ=0、cosθ=1、cosθ=1/2のときのθの値の求め方・計算方法について解説していきます。
数学が苦手、三角関数が苦手な人でも理解できるようわかりやすく解説していますので、ぜひ最後までお読みください。
※三角比(sin・cos・tan)の基礎がまだ不安な人は三角比の覚え方について解説した記事をまずはお読みください。
cosθ=0の求め方・計算方法
まずはcosθ=0から解いていきましょう。
cosθ=0やsinθ=1など、θの値を求めるには単位円を使うのが一般的です。
なので、まずは単位円のおさらいを軽くしておきましょう。
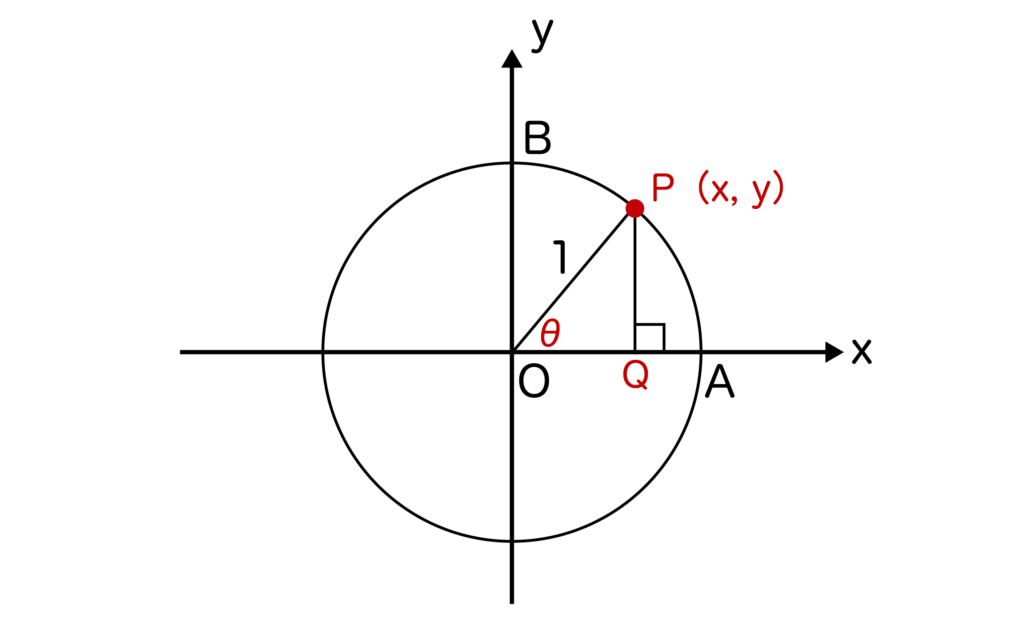
単位円とはxy平面において原点Oを中心とした半径=1の円のことでしたね。そして、以下の図においてAO=0度としてθを取ったとき、sinθ=y、cosθ=xが成り立つのでした。
※sinθ=PQ/OP=PQ=y、cosθ=OQ/OP=OQ=xより
なので、cosθ=0を解くときは、単位円上にx=0を引いてみることから始めましょう。単位円上にx=0を引くと以下の赤線のようになりますね。
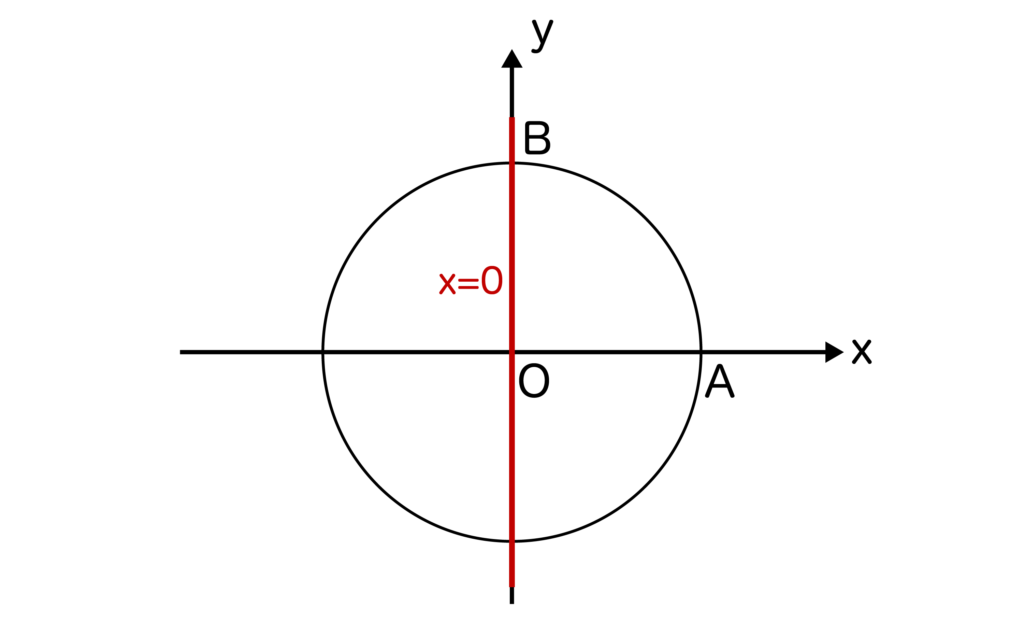
すると、θ=∠AOBとなるのでθ=90度であることがわかります。
まだ単位円の使い方が掴めていない人も多いと思うので、もう1つ例題を解いてみましょう。
cosθ=1の求め方・計算方法
次はcosθ=1のときのθを求めてみます。
今回はcosθ=1なので、x=1を単位円上に取ってみます。
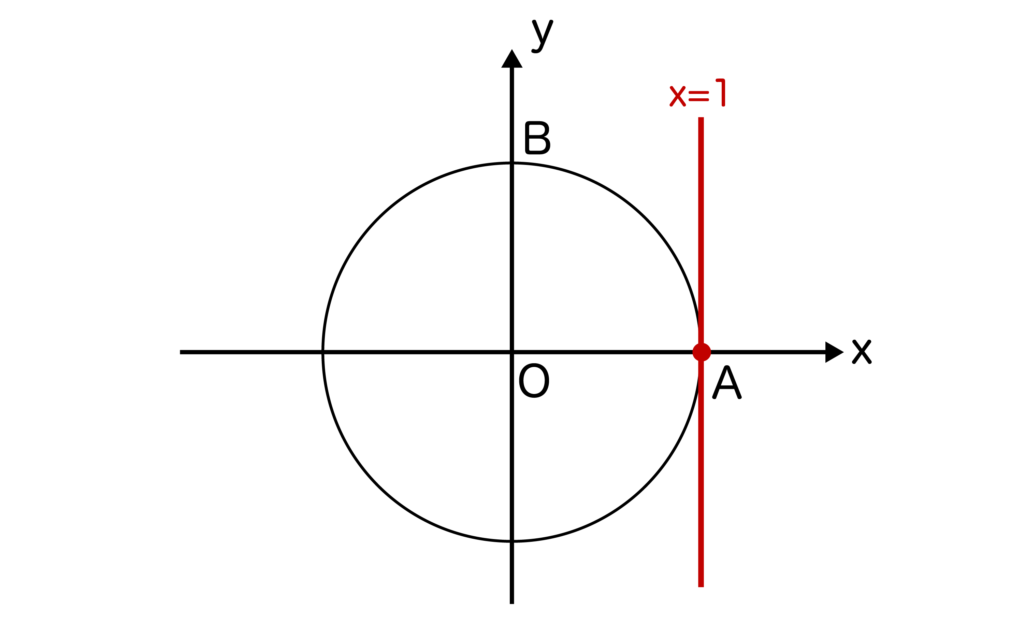
すると、単位円とx=1は点Aだけで交わることがわかりますね。
よって求めるθ=AO=0度となります。
もう1つ例題を解いてみましょう。
cosθ=1/2の求め方・計算方法
最後はcosθ=1/2のθを求めてみましょう。
x=1/2を単位円上に引いてみます。そして、以下の図のように単位円との交点をPとR、x軸との交点をQとします。
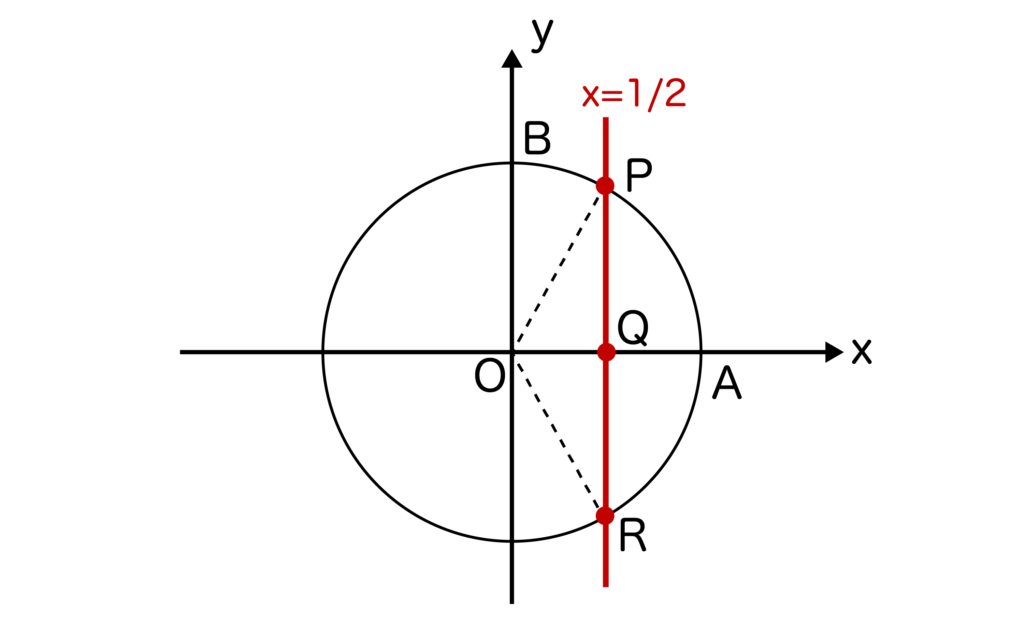
すると、OQ=1/2ですね。また、単位円なのでOP=1です。
したがって、OQ:OP=1:2であり、∠OQP=90度なので三角形OPQは辺の比が1:2:√3の直角三角形であることがわかります。
同様に考えて、三角形ORQも辺の比が1:2:√3の直角三角形であることがわかります。
よって、∠AOP=60度となるので、求めるθ=60度となります。
また、∠AORも60度なので、求めるθ=360度-60度=300度となります。
つまり、cosθ=1/2となるθの値は0度<θ<360度においては60度と300度になります。
cosθ=aを解く手順としては、
- 単位円上にx=aを引く
- x=aと単位円との交点を見つけて、その交点と原点O、x軸との角度を求める
という流れになります。
単位円を使ったθの求め方は三角関数の基本であり、非常に重要です。必ずできるようにしておきましょう。
単位円にもっと慣れたい人はsinθ=1やsinθ=1/2の求め方について解説した記事もぜひ合わせてご覧ください。
cosθ=0、1、1/2のときのsinθとtanθ
以上をまとめると、
- cosθ=0のとき、θ=90度
- cosθ=1のとき、θ=0度
- cosθ=1/2のとき、θ=60度、300度
となります。それぞれのθにおけるsin、tanの値もついでに求めてみましょう。
まず、θ=90度からです。θ=90度のときsinθ=1ですね。
※詳しくはsin90度が1なのはなぜかについて解説した記事をご覧ください。
tanθですが、ここでtanθ=sinθ/cosθの公式を使います。
※tanθ=sinθ/cosθがわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
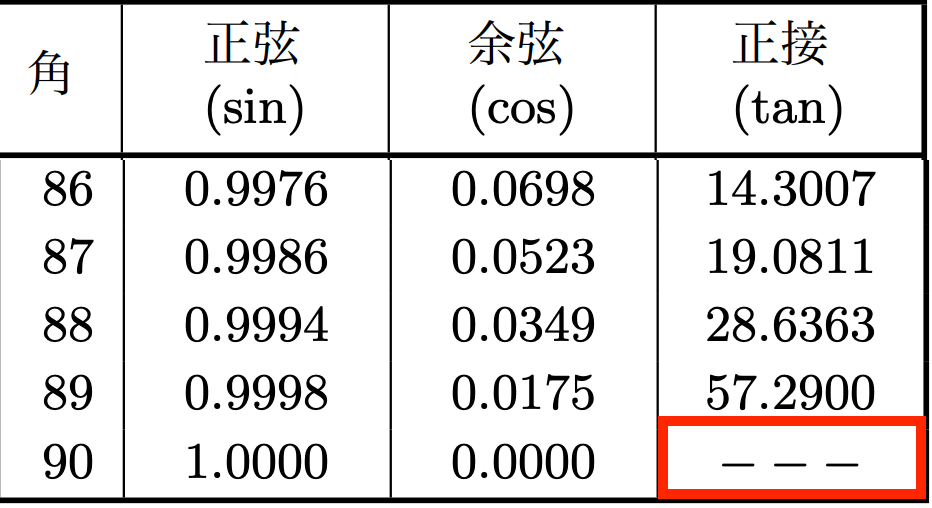
tan90度=sin90度/cos90度=1/0=計算不可となります。
分数において分母=0は認められておらず、計算不可となるのでした。なので、tan90度は定義することができません。
※tan90度はなぜ値がないかについて詳しく解説した記事もぜひ合わせてご覧ください。
実際に三角比の表を見てもtan90度の値は記載されていないことがわかります(以下参照)
※三角比の表の見方がわからない人は三角比の表の見方について解説した記事をご覧ください。
次はθ=0度のときです。sin0度=0ですね。
※詳しくはsin0度の求め方について解説した記事をご覧ください。
tan0度=sin0度/cos0度=0/1=0となります。
※tan0度について詳しく解説した記事もぜひ合わせてご覧ください。
続いてはθ=60度です。
sin60度=√3/2ですね。
※詳しくはsin60度の求め方について解説した記事をご覧ください。
したがって、tan60度=sin60度/cos60度=√3/2 ÷ 1/2=√3となります。
※tan60°が√3になる理由3つについて解説した記事もぜひ合わせてご覧ください。
最後はθ=300度です。θ=300度を単位円に取ると以下のようになるのでした。
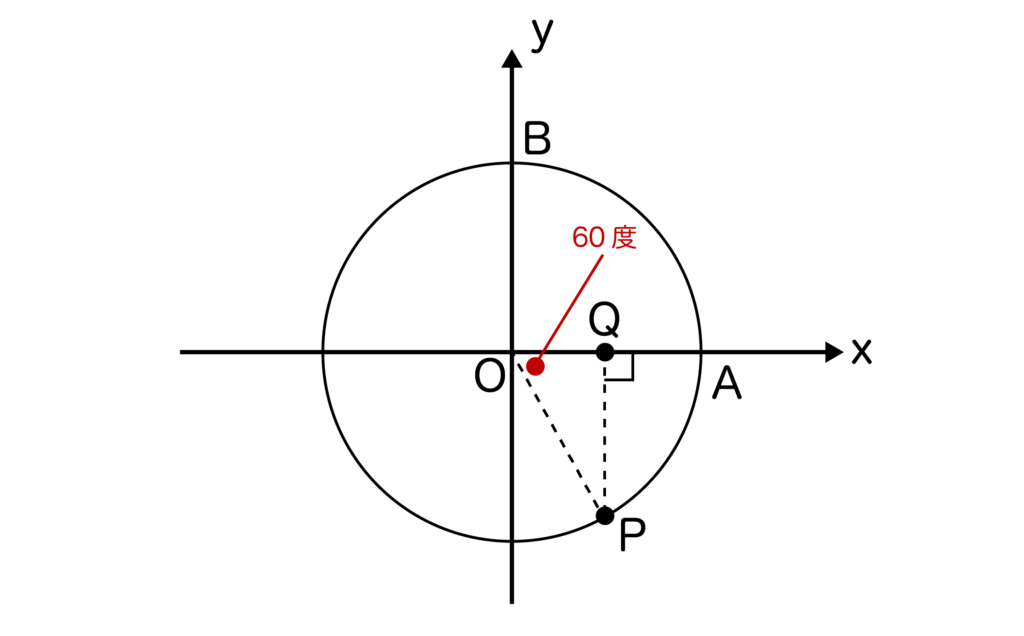
上記でも解説した通り、三角形OPQは辺の比が1:2:√3の直角三角形であり、OP=1なのでOQ=1/2、QP=√3/2となりますね。
つまり、点Pの座標は(1/2、-√3/2)となります。y座標はマイナスであることにご注意ください。
よって、sin300度=点Pのy座標=-√3/2となります。
したがって、tan300度=sin300度/cos300度=-√3/2 ÷ (1/2)=-√3となります。
いかがでしたでしょうか?
今回はcosθ=0、1、1/2の求め方・計算方法について解説しました。
繰り返しにはなりますが、単位円は大学入試や共通テストでも頻出です。必ず使えるようにしておいてください。


