「三角形の成立条件を答えよ」と言われて、皆様はすぐに答えられますでしょうか?
三角形の成立条件はこれから三角関数の学習を進めていく上で重要な公式の1つです。
そこで今回は早稲田大学教育学部数学科を卒業した筆者が三角形の成立条件とは何か(辺の長さの関係)について解説した後、三角形の成立条件の証明も行います。
最後には三角形の成立条件に関する練習問題も用意しているので、ぜひ最後までお読みください。
三角形の成立条件とは?公式
三角形の成立条件とは、三角形の2辺の長さの和は他の1辺の長さよりも大きいことを言います。
例えば、以下の三角形ABCを見てみましょう。
-1024x258.png)
AB=10ですね。残りの2辺の和AC+BC=6+15=21なので、三角形の成立条件が成り立っていることがわかります。
次はACに注目してみましょう。AC=6ですね。残りの2辺の和AB+BC=10+15=25なので、こちらに関しても三角形の成立条件が成り立っていることがわかります。
最後はBCに注目してみましょう。BC=15ですね。残りの2辺の和AB+AC=10+6=16なので、こちらに関しても三角形の成立条件が成り立っていることがわかります。
ここで、三角形の成立条件を一般化しておきましょう。
以下のように三角形ABCにおいて、頂点A、B、Cに向かい合う辺(対辺といいます)BC、CA、ABの長さをそれぞれa、b、cとします。
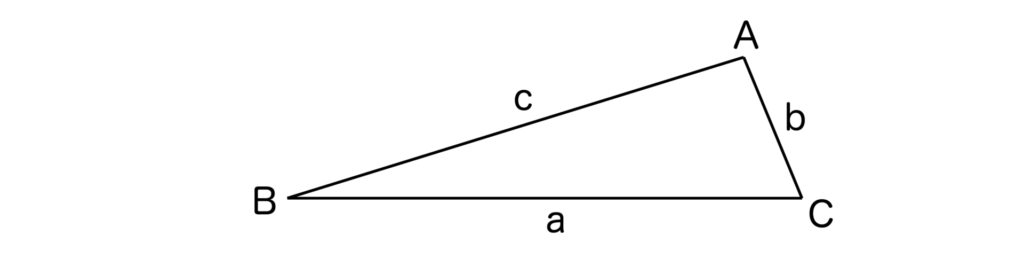
すると、|b-c|<a<b+cが成り立ちます。
以上は三角形の成立条件の公式として必ず覚えておきましょう。
三角形の成立条件の証明
ここからは三角形の成立条件の証明(成り立つ理由)について解説していきます。
三角形の成立条件の証明は三角比を使うことで証明できます。
※三角比がわからない人は三角比の覚え方について解説した記事をご覧ください。
【証明】
以下の図のような三角形ABCを用いて三角形の成立条件の証明を行なっていきます。
頂点AからBCに垂線AHを下ろすと、cosC=HC/bより、HC=bcosCとなりますね。
同様に考えて、cosB=BH/cより、BH=ccosBを得ることができます。
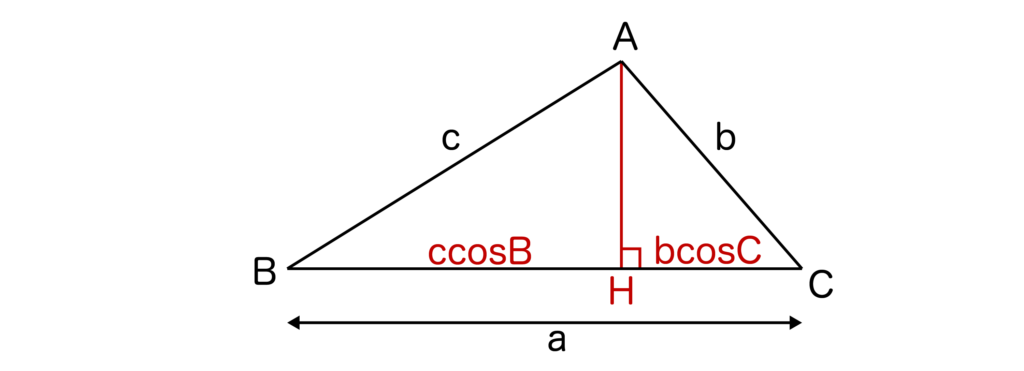
ここで、
- -1<cosB<1、-1<cosC<1
- a=ccosB+bcosC
なので、b+c-a=b+c-(ccosB+bcosC)=b(1-cosC)+c(1-cosB)>0となりますね。
よって、a<b+cとなります。
同様に考えて、b<c+a、c<a+bが成り立ちます、
また、b<c+a、c<a+bからb-c<aかつc-b<aとなります。
この2つは|b-c|<aとまとめることができるので、|b-c|<a<b+cが成り立ちます。
※同様に、|c-a|<b<c+a、|a-b|<c<a+bとなります。
以上が三角形の成立条件の証明となります。
三角形の成立条件の証明自体は大学入試や共通テストで出題される可能性はかなり低いので暗記する必要はありませんが、三角形の成立条件の公式は必ず覚えておきましょう。
三角形の成立条件に関する練習問題
最後に、三角形の成立条件に関する練習問題を用意しました。
以上で学習したことを踏まえて解いてみましょう。
【練習問題1】
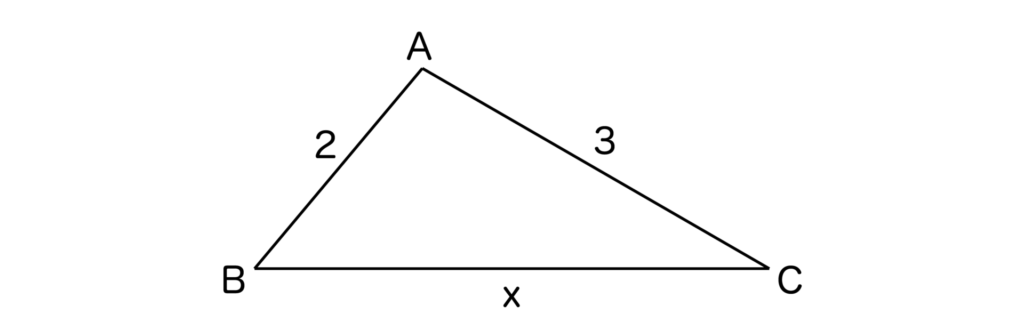
AB=2、BC=x、CA=3の三角形ABCがある。
(1)xのとりうる値の範囲を求めなさい。
(2)三角形ABCが鈍角三角形となるとき、xのとりうる値の範囲を求めなさい。
【解答&解説】
(1)三角形の成立条件の公式より、
|3-2|<x<3+2が成り立つので、1<x<5・・・(答)
※|x-3|<2<x+3 または |2-x|<3<2+xを解いても問題ありませんが、計算が面倒なので|3-2|<x<3+2にしましょう。
(2)どの辺が最大の長さの辺になるのかで場合分けして考えます。
[1]1<x<3のとき、最大辺=3となるので、その対角が90度より大きいと鈍角三角形になります。
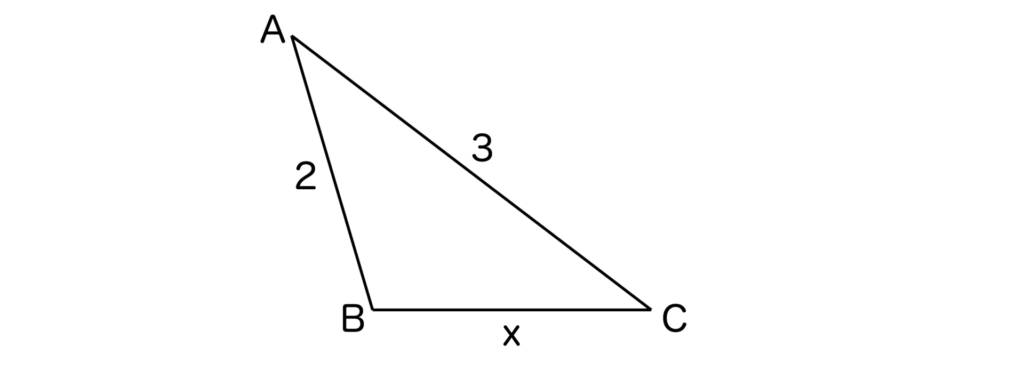
このとき、三角形の辺と角の大小の関係より、B>90° ⇔ AC2>AB2+BC2となりますね。
※三角形の辺と角の大小について解説した記事もご用意しているので、ぜひ参考にしてください。
したがって、32>22+x2よりx2-5<0が成り立ちます。
よって、-√5<x<√5となります。
※二次不等式の解き方がわからない人は二次不等式の解き方について解説した記事をご覧ください。
1<x<3との共通範囲を求めて、1<x<√5となります。
[2]3≦x<5のとき、最大辺=xとなるので、その対角が90°よりも大きいと鈍角三角形になります。
よって、x2>22+32より、x2-13>0となるので、x<-√13、√13<xとなります。
3≦x<5との共通範囲を求めて、√13<x<5となります。
答えは[1]と[2]を合わせて、1<x<√5、√13<x<5・・・(答)となります。
【練習問題2】
AB=x、BC=x-3、CA=x+3の三角形ABCがある。
(1)xのとりうる値の範囲を求めなさい。
(2)三角形ABCが鋭角三角形となるとき、xのとりうる値の範囲を求めなさい。
【解答&解説】
(1)x>0であることから、CAが最大辺となりますね、
よって、三角形の成立条件の公式よりx+3<x+(x-3)となるので、x>6・・・(答)
(2)CAが最大辺であることから、三角形ABCが鋭角三角形であるとき∠B<90°が成り立ちます。
よって、AC2<AB2+BC2より、(x+3)2<x2+(x-3)2
整理して、x2-12x>0より、x<0、12<x
(1)よりx>6であるからx>12・・・(答)となります。
いかがでしたか?
今回は三角形の成立条件の公式と証明、三角形の成立条件に関する練習問題をご紹介していきました。
三角形の成立条件の公式は割と忘れがちなので、これを機にしっかりと覚えておきましょう。