因数分解は中学数学でも学習したかと思いますが、高校数学でも登場します。
因数分解は大学入試や共通テストでも頻出なので、勉強・対策の優先度はかなり高いです。
そこで本記事では、早稲田大学教育学部数学科を卒業した筆者が数学1で学習する因数分解の公式やたすき掛けのコツ、入試で使えるテクニックや応用問題をご紹介していきます。
数学が苦手な高校生でも理解できるようわかりやすく解説しているので、ぜひ参考にしてください。
数学1:因数分解の公式
まずは因数分解とは何かについて簡単に解説します。
因数分解とは1つの多項式を、1次以上の多項式の積(=掛け算)の形に変形することです。
※多項式が理解できていない人は、多項式の定義について解説した記事をご覧ください。
例えば、多項式a2+5a+6があったとします。これは(a+2)×(a+3)と表現することができます。
実際に(a+2)×(a+3)を分配法則を使って計算してみると、
(a+2)×(a+3)
=a2+3a+2a+6
=a2+5a+6となっていることがわかります。
※分配法則については多項式の計算方法について解説した記事をご覧ください。
つまり、多項式a2+5a+6は(a+2)と(a+3)の積で表現できるので、「a2+5a+6を因数分解せよ」と言われたら(a+2)(a+3)が答えとなります。
ちなみに、積を作っている各式のこと因数と呼びます。上記の例だと、(a+2)と(a+3)が因数となります。
因数分解では、ma+mb=m(a+b)のように、各項に共通な因数があれば、その共通の因数をかっこ()の外にくくり出すのが基本です。
例えば、2a2+6a+4=(2a+4)(2a+1)と因数分解することができますが、因数(2a+4)は2をかっこの外に出せるので2(a+2)とする必要があります。
よって、最終的な答えは2(a+2)(2a+1)となります。
因数分解とは何かを理解できたら、数学1で登場する以下5つの因数分解の公式を覚えましょう。
- a2+2ab+b2 = (a+b)2
- a2-2ab+b2 = (a-b)2
- a2-b2 = (a+b)(a-b)
- x2+(a+b)x+ab = (x+a)(x+b)
- acx2+(ad+bc)x+bd = (ax+b)(cx+d)
5つ目の公式は覚えにくいですが、後ほどご紹介するたすき掛けのやり方やコツを覚えて問題をたくさん解けば自然に覚えている状態になるので、今の時点ではあまり気にしなくても大丈夫です。
数学1:因数分解のたすき掛け
次数が2の項(x2やa2など)の係数が1ではない多項式ax2+bx+cの因数分解は上記でご紹介した因数分解の公式acx2+(ad+bc)x+bd = (ax+b)(cx+d)を利用して行います。
例えば、3x2+5x+2を因数分解することを考えてみましょう。
手順としては以下の3つとなります。
手順1
まずはx2の係数である3と定数項2に注目します。
そして、3=ac、2=bdとなる数の組(a、c)(b、d)を考えます。
※a、b、c、dはすべて正の整数とします。組み合わせは複数存在するケースが多いです。
すると、
(a、c)=(1、3)(3、1)
(b、d)=(1、2)(2、1)
となりますね、
手順2
手順1で求めた(a、c)(b、d)のうち、xの係数である5=ad+bcとなるa、b、c、dを探します。
すると、a=1、b=1、c=3、d=2であることがわかります。
※a=3、b=2、c=1、d=1でも問題ありませんが、今回は上記で進めてみます(答えは同じになるのでご安心ください)
探し方としては、以下のような図を書くと見つけやすいです(これをたすき掛けと言います)
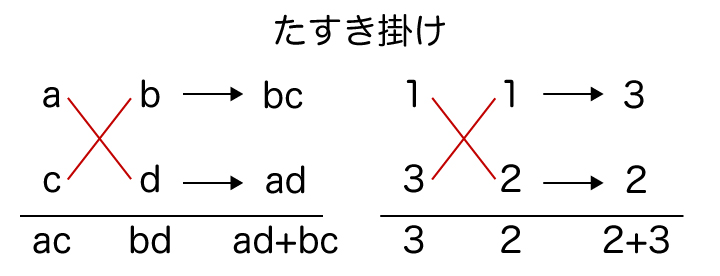
手順3
手順2で求めたa、b、c、dを(ax+b)(cx+d)に代入して因数分解完了です。
つまり、3x2+5x+2を因数分解すると(x+1)(3x+2)となります。
ちなみに、a=3、b=2、c=1、d=1とした場合は(3x+2)(x+1)となりますが、いずれにせよ答えは同じになります。
因数分解のたすき掛けのコツ
たすき掛けでは複数の組み合わせが存在するケースがほとんどなので、効率よくa、b、c、dを見つける必要があります。
因数分解の問題をたくさん解いていくうちに組み合わせを見つけるスピードは確実に早くなるので、問題をたくさん解くというのが一番の近道ではあるのですが、コツを1つご紹介しておきます。
例えば、6x2+x-2を因数分解することを考えてみましょう。
ac=6、bd=-2より、組み合わせとしては以下8通りが考えられます。
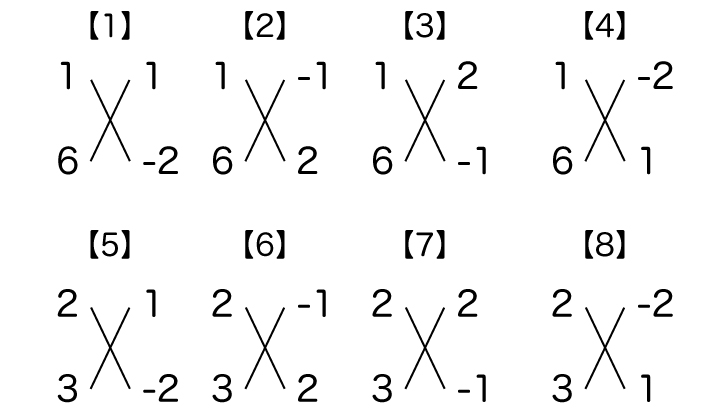
以上8通りのうち、【1】【2】【7】【8】は横に並んだ2つの数が1以外の約数を持つため、候補外であることがわかります(以下の図参照)
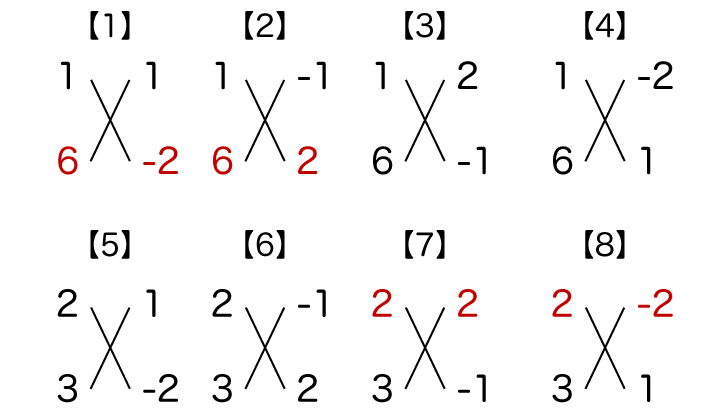
例えば【1】の場合だと(x+1)(6x-2)が答えになりますね。しかし、(6x-2)は2(3x-1)となり、2でくくり出せますが、もとの多項式6x2+x-2は2でくくり出すことができないので【1】の組み合わせで因数分解できることはありえないということになります。
以上より、【3】【4】【5】【6】の中から適した組み合わせを探せば良くなるので、少し効率が良くなります。
「くくり出せる組み合わせは選ばない」というコツはかなり有効なので、ぜひ覚えてください。
置き換えを利用した因数分解
多項式に同じ形の式が含まれているものは置き換えを利用するとスムーズに因数分解できます。
例えば、(x2+x-5)(x2+x-7)+1を因数分解してみましょう。
x2+xという式が2つ存在しているので、x2+x=Aとおいてみます。
すると、(x2+x-5)(x2+x-7)+1
=(A-5)(A-7)+1
=A2-12A+35+1
=A2-12A+36
=(A-6)2
となります。ここで、Aをx2+xに戻して、
(x2+x-6)2
={(x-2)(x+3)}2・・・(答)となります。
置き換えは大学入試・共通テストでも頻出のテクニックなので、必ず覚えておきましょう。
最低次の文字に注目した因数分解
2つ以上の文字を含む多項式は最低次の文字に注目すると因数分解できるケースがあります。
例えば、3ab+9b2-2a-4を因数分解してみましょう。
aとbという2つの文字が含まれており、aの次数=1、bの次数=2なのでaについて降べきの順に整理してみます。
すると、(3b-2)a+9b2-4となりますね。
※降べきの順の整理する方法について解説した記事もぜひ合わせてご覧ください。
9b2-4=(3b+2)(3b-2)と因数分解できるので、
(3b-2)a+9b2-4
=(3b-2)a+(3b+2)(3b-2)
=(3b-2)(a+3b+2)・・・(答)となります。
最低次の文字に注目した因数分解もよく使うテクニックなので、必ず覚えておきましょう。
平方の差を作る因数分解
2乗-2乗の形(a2-b2など)を作ることができれば(a+b)(a-b)のように因数分解できます。
上手く2乗-2乗の形を作れないか?に注目してみるのも1つのテクニックです。
例えば、x4+4x2+16を因数分解してみましょう。
x4+4x2+16
=(x4+8x2+16)-4x2
=(x2+4)2-(2x)2
=(x2+2x+4)(x2-2x+4)・・・(答)
となります。
因数分解の練習問題
以上で数学1の因数分解で必要な公式やテクニックはすべてご紹介しました。
ここからはたくさんの練習問題を解いて因数分解に慣れていくのみです。
【練習問題】
以下の多項式を因数分解せよ。
(1)(x-y)2-zx+yz
(2)x2+8x+16
(3)9x2-12xy+4y2
(4)x2+12x+32
(5)2x2-9x+4
(6)2(x-1)2-11(x-1)+15
(7)x3-x2y-xz2+yz2
(8)4x4+1
【解答&解説】
(1)(x-y)2-zx+yz
=(x-y)2-z(x-y)
=(x-y)(x-y-z)・・・(答)
(2)x2+8x+16
=(x+4)2・・・(答)
(3)9x2-12xy+4y2
=(3x-2y)2
(4)x2+12x+32
=(x+4)(x+8)・・・(答)
(5)たすき掛けの問題となります。
以下でたすき掛けができます。
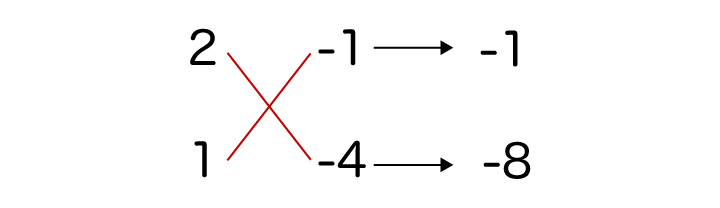
よって、2x2-9x+4
=(2x-1)(x-4)・・・(答)
(6)(x-1)が共通しているので、(x-1)=Aとおいてみましょう。
すると、2(x-1)2-11(x-1)+15
=2A2-11A+15
=(2A-5)(A-3)
ここで、Aをx-1に戻して、(2x-7)(x-4)・・・(答)となります。
(7)xの次数=3、yの次数=1、zの次数=2なので、yについて降べきの順に整理してみましょう。
x3-x2y-xz2+yz2
=(z2-x2)y+x3-xz2
=(z2-x2)y-x(z2-x2)
=(z2-x2)(y-x)
=(z+x)(z-x)(y-x)・・・(答)
(8)平方の差を作れないか考えてみましょう。
4x4+1
=(4x4+4x2+1)-4x2
=(2x2+1)2-(2x)2
=(2x2+1+2x)(2x2+1-2x)
=(2x2+2x+1)(2x2-2x+1)・・・(答)
今回は高校数学の数学1が学習する因数分解の公式や大学入試・共通テストで活用できるテクニックなどをご紹介していきました。
因数分解は高校数学の基礎なので、必ずできるようにしておきましょう。問題集や参考書でたくさんの問題を解いて慣れていってください。


