余弦定理は正弦定理と一緒に学習することが多い、三角関数の分野で非常に重要な公式です。
余弦定理は正弦定理と同じく、大学入試や共通テストでも頻出です。
本記事では、早稲田大学教育学部数学科を卒業した筆者が余弦定理とは何か?公式や証明、余弦定理を使って面積を求める方法など余弦定理に関して知っておくべき情報を完全網羅しました。
最後には余弦定理に関する練習問題も用意しているので、ぜひ最後までお読みください。
余弦定理とは?公式
まずは余弦定理とは何か?余弦定理の公式から解説していきます。
以下のように三角形ABCにおいて、頂点A、B、Cに向かい合う辺(対辺といいます)BC、CA、ABの長さをそれぞれa、b、cとします。また、∠A、∠B、∠Cの大きさをそれぞれA、B、Cとします。
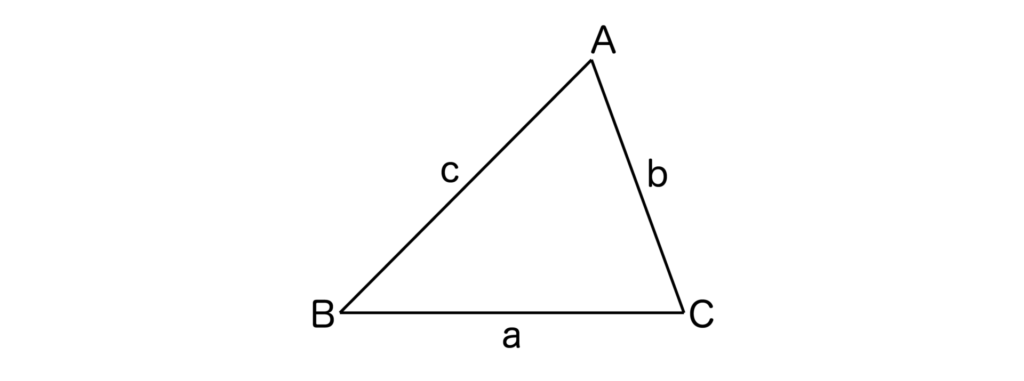
すると、三角形ABCにおいて
- a2=b2+c2-2bccosA
- b2=c2+a2-2cacosB
- c2=a2+b2-2abcosC
が成り立ちます。これを余弦定理と言います。冒頭でも解説した通り、余弦定理は正弦定理と同様に大学入試や共通テストで頻出です。必ず暗記しておきましょう。
※正弦定理について詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
また、以上の余弦定理の公式を変形することで以下の式を得ることができます。
- cosA=(b2+c2-a2)/2bc
- cosB=(c2+a2-b2)/2ca
- cosC=(a2+b2-c2)/2ab
この式も非常によく使うので、余弦定理と一緒に覚えておきましょう。
ちなみにですが、正確にいうと以上の余弦定理は第二余弦定理と呼ばれています。
「第二」というくらいなので、もちろん第一余弦定理もあります。第一余弦定理については後ほど解説していきます。
余弦定理の証明(成り立つ理由)
ここからは余弦定理(第二余弦定理)の証明(余弦定理が成り立つ理由)について解説していきます。
【証明】
以下の図のようにxy平面上に三角形ABCを取ります。
A(0、0)、B(c、0)とすると、C(bcosA、bsinA)となりますね。
※cosA=AH/bより、AH=bcosA=点Cのx座標となります。同様に考えて、sinA=CH/bより、CH=bsinA=点Cのy座標となります。sin、cosの求め方がわからない人は三角比の覚え方について解説した記事をご覧ください。
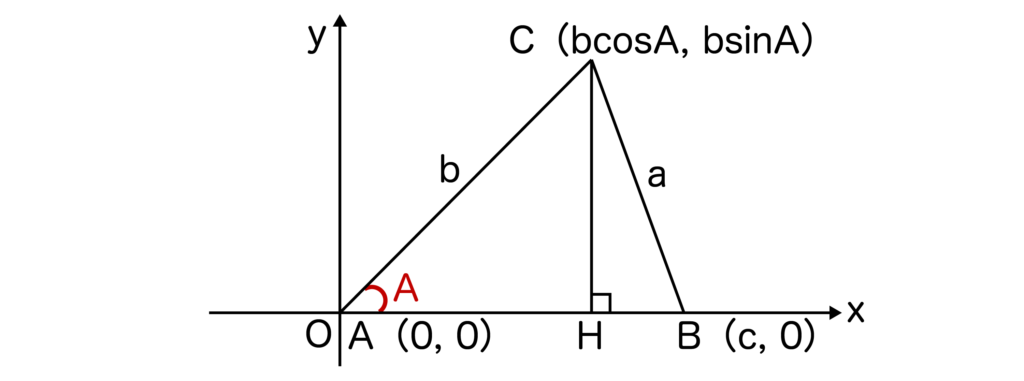
ここで直角三角形BCHに注目すると、三平方の定理より
BC2=BH2+CH2
が成り立ちますね。ゆえに、
a2
=|c-bcosA|2+(bsinA)2
=c2-2bccosA+b2(cos2A+sin2A)
=b2+c2-2bccosA・・・①
となります(cos2θ+sin2θ=1でしたね。詳しくは三角比の関係式・相互関係について解説した記事をご覧ください)
①においてa→b、b→c、c→a、A→Bとすると、
b2=c2+a2-2cacosB
さらに、b→c、c→a、a→b、B→Cとすると、
c2=a2+b2-2abcosC
となります。以上より、余弦定理の証明ができました。
余弦定理の覚え方
ここからは余弦定理(第二余弦定理)の覚え方をご紹介します。余弦定理を改めて以下に書いてみます。
- a2=b2+c2-2bccosA
- b2=c2+a2-2cacosB
- c2=a2+b2-2abcosC

例えば、a2=b2+c2-2bccosAだとaを求めるには両端の辺の2乗の和から2bc・cosAを引けば良いですね。
求めたい辺の両端にある辺の和の2乗から、2×両辺×cos(求めたい辺の対角)と覚えましょう。
しかし、無理に覚える必要はありません。これから先の三角関数の学習で余弦定理は何回も使います。
何回も使えば自然に公式は覚えている状態になります。なので、現時点では無理に余弦定理の公式を覚えようとはせず、たくさんの練習問題を解くことを意識してください。
第一余弦定理とは?
以上は第二余弦定理に関する解説でした。
第一余弦定理は三角形の辺の長さと三角比との関係を表すもので、以下の公式のことを言います。
三角形ABCにおいて、
- a=ccosB+bcosC
- b=acosC+ccosA
- c=bcosA+acosB
が成り立つ。

証明もしておきましょう。a=ccosB+bcosCを示します。
【証明】
[1]0°<C<90°のとき
以下の図のように頂点AからBCに垂線AHを下ろします。
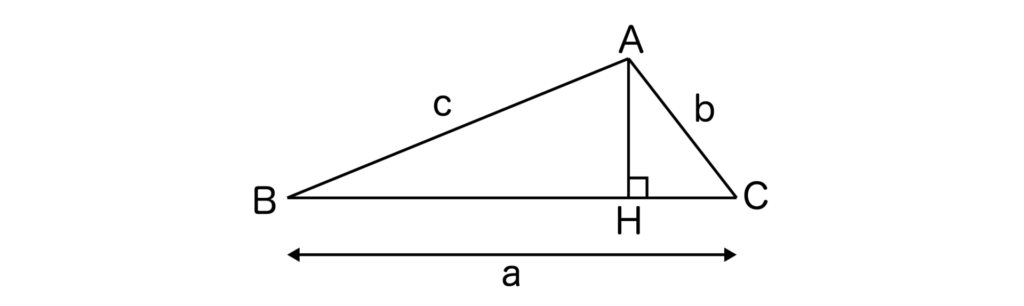
すると、a=BC=BH+HC=ccosB+bcosCとなることがわかります。
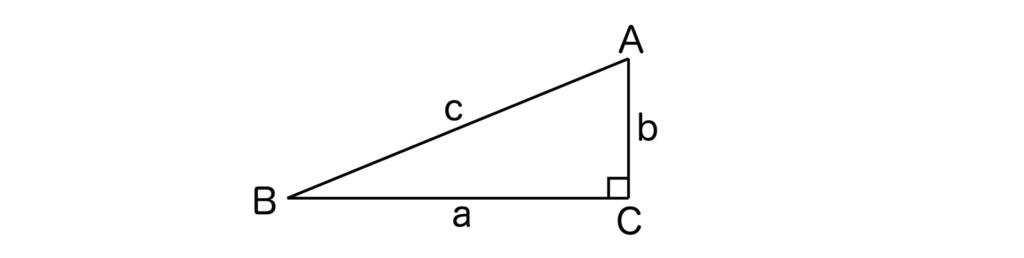
[2]C=90°のとき
cosB=a/c、cosC=0であるから、a=ccosB+bcosCが成り立ちます。
[3]90°<C<180°のとき
頂点Aから直線BCに垂線AHを下ろします。
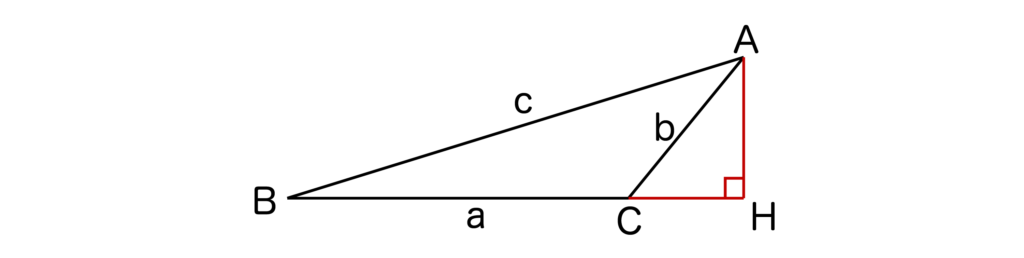
すると、a=BC=BH-HCですね。
また、BH=ccosB、CH=bcos(180°-C)=-bcosCなので、
a=BH-HC=ccosB+bcosCとなります。
以上より、a=ccosB+bcosCが成り立ちます。
b=acosC+ccosA、c=bcosA+acosBも同様に示すことが可能です。
以上が第一余弦定理の公式と証明になります。一般的な余弦定理(=第二余弦定理)と一緒に覚えておくと便利です。
余弦定理で角度と面積を求めてみよう
ここからは余弦定理(第二余弦定理)の活用シーンをご紹介していきます。
余弦定理を使えば、3辺の情報から角度と面積を求めることができます。では、例題をみてみましょう。
【例題】
以下の三角形ABCにおいて角Aの大きさと三角形ABCの面積を求めよ。
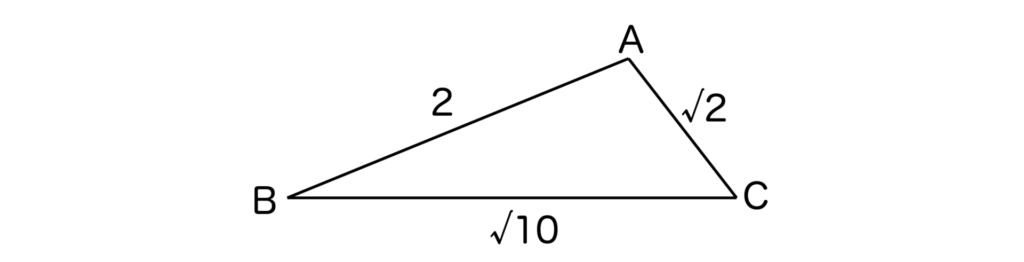
【解答&解説】
余弦定理より、
cosA=(√2)2+22-(√10)2 / 2・√2・2=-1/√2
したがって、A=135度・・・(答)
※cosA=-1/√2からA=135度になる理由がわからない人は、cosθの求め方について解説した記事をご覧ください。
また、三角形ABCの面積=1/2・2・√2・sin135度=1/2・2・√2・1/√2=1・・・(答)
※三角形ABCの面積=1/2・bc・sinAで求められるのでした。詳しくは三角形の面積の求め方の公式3つをご紹介した記事をご覧ください。
※sin135度の求め方について解説した記事もぜひ参考にしてください。
三角形の3辺から角度を求めて、面積を求めるというのは余弦定理のよくある使い方です。必ずできるようにしておきましょう。
余弦定理の練習問題
最後に余弦定理の練習問題を2問解いてみましょう。
これ以外にも数学の教科書や参考書などでたくさんの余弦定理の問題を解いて、1日も早く余弦定理を覚えてしまいましょう。
【練習問題】
(1)三角形ABCにおいて、A=60度、b=5、c=3のときaの値を求めよ。また、三角形ABCの面積も求めよ。
(2)三角形ABCにおいて、a=√2、b=2、A=30度のとき、c、B、Cを求めよ。
【解答&解説】
(1)余弦定理より、
a2=b2+c2-2bccosAなので、
a2=52+32-2・5・3・cos60°=25+9-2・5・3・1/2=19
a>0なので、a=√19・・・(答)となります。
また、三角形ABCの面積=1/2・5・3・sin60度=1/2・5・3・√3/2=15√3/4・・・(答)となります。
※sin60度=1/2です。詳しくはsin60度、sin-60度の値について解説した記事をご覧ください。
(2)余弦定理より、
(√2)2=22+c2-2・2・c・cos30度
よって、c2-2√3c+2=0となるので、c=√3±1となります。
※c=√3±1となる理由がわからない人は解の公式について解説した記事をご覧ください。
[1]c=√3+1のとき
余弦定理より、
cosB=(√3+1)2+(√2)2-22 / 2(√3+1)・√2=1/√2
となるので、B=45度となります。よって、C=180度-30度-45度=105度となります。
[2]c=√3-1のとき
余弦定理より、
cosB=(√3-1)2+(√2)2-22 / 2(√3-1)・√2=-1/√2
となるので、B=135度となります。よって、C=180度-30度-135度=15度となります。
[1]と[2]より、
- c=√3+1のとき、B=45°、C=105°
- c=√3-1のとき、B=135°、C=15°
となります。
【別解】
第一余弦定理を使って求めることも可能です。
正弦定理より、
2/sinB=√2/sin30°が成り立つので、sinB=1/√2となりますね。
A=30度より、0度<B<150度なので、B=45度、135度が求まります。
[1]B=45度のとき
C=180度-30度-45度=105度
第一余弦定理より、c=bcosA+acosB=2cos30°+√2cos45°=√3+1
[2]B=135度のとき
C=180度-30度-135度=15度
第一余弦定理より、c=bcosA+acosB=2cos30°+√2cos135°=√3-1
となります。
以上のように、2辺と対角(2辺とその間以外の1つの角)の条件が与えられたときは三角形が1通りに定まるとは限らないのでご注意ください。
以上のように第二余弦定理を使う場合は余弦定理を活用してcについての二次方程式を作って解き、正の解が2つ得られたら、それぞれについて場合分けを行うことで残りの角を求める必要があります。
※二次方程式の解き方3パターンについて解説した記事もぜひ合わせてご覧ください。
いかがでしたでしょうか?
今回は余弦定理とは何か・公式・証明・面積の求め方について解説していきました。
ぜひ正弦定理とセットでたくさんの問題を解いて余弦定理に慣れていってください。