皆様はsin135度とcos135度の値を自力で求めることができますでしょうか?
中にはsin135度とcos135度の値を暗記している人もいるかもしれませんが、三角比(sin・cos・tan)の値を暗記だけに頼るのは非常に危険です。いつでも自力で値を求められるようにしておかないとこの先の三角関数の学習でつまずいてしまいます。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin135度とcos135度の求め方について図解で解説していきます。
ぜひ最後までお読みいただき、自力で三角比を求められるようにしておきましょう。
sin135度とcos135度の求め方
sin135度やcos135度のように、sinθ、cosθのθが90度を超える場合は単位円を使ってその値を求めるのが定石です。
単位円とはxy平面上において、原点Oを中心とした半径=1の円のことを指すのでした。
そして、以下の図のように単位円の円周上に点P(x、y)を取ると、sinθ=y、cosθ=xが成り立つのでしたね。
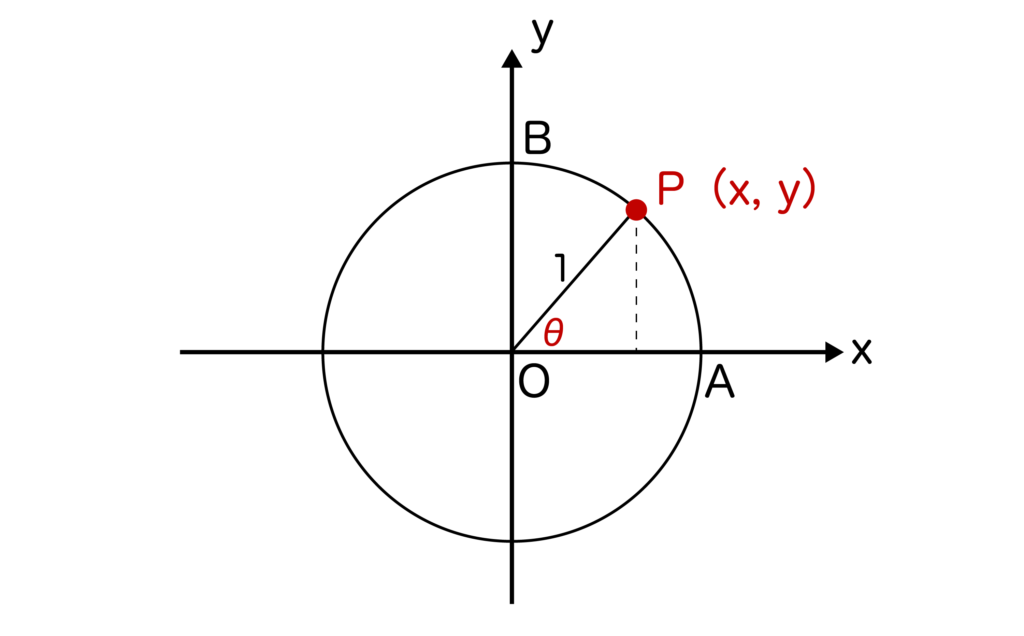
※sinθ=y、cosθ=xが成り立つ理由についてはsin90度が1なのはなぜかについて解説した記事をご覧ください。
つまり、点Pのy座標がsinθに該当し、点Pのx座標がcosθに該当するということです。
以上を用いてsin135度とcos135度の値を求めてみましょう。
まずは単位円上にθ=135度を取ります。そして、点Pからx軸に垂線をおろし、その垂線とx軸との交点をQとします。単位円なので、OP=1となります。
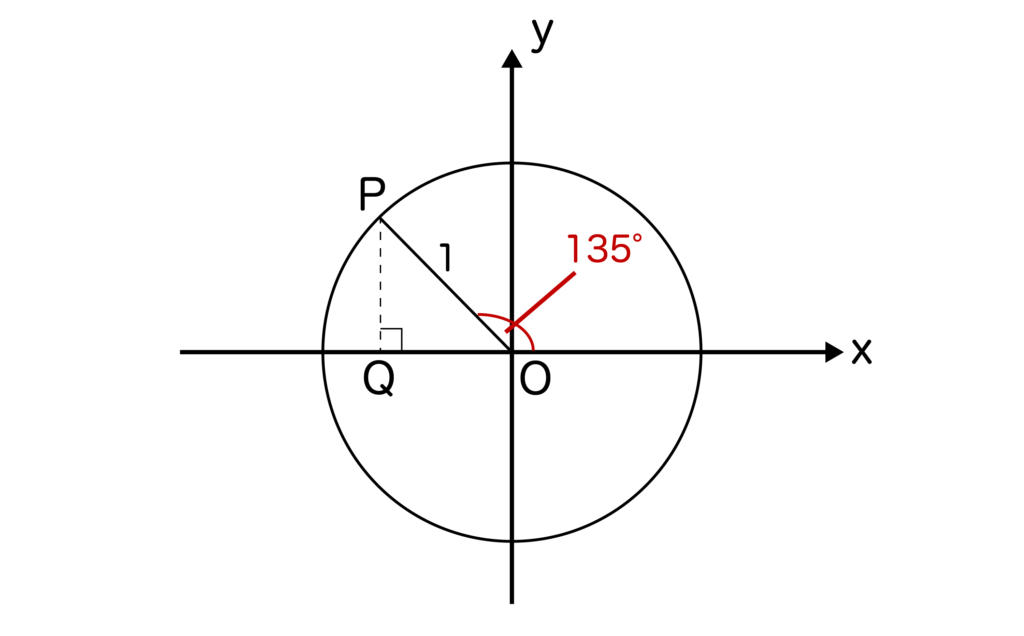
すると、∠QOP=180度-135度=45度となりますね。
つまり、三角形OPQはOQ:PQ:OP=1:1:√2の直角三角形であることがわかります。
OP=1なので、PQ=OQ=1/√2となります。
つまり、点P(-1/√2、1/√2)であることがわかりました。
したがって、
- sin135度=点Pのy座標=1/√2
- cos135度=点Pのx座標=-1/√2
となります。1/√2や-1/√2は分母の有利化を行っても問題はありませんが、そのままでも十分綺麗な分数の形なので有利化を行う必要は特にありません。
以上が単位円を活用したsin135度、cos135度の求め方となります。
単位円はこれからより深く三角関数の学習を進めていくとわかりますが、非常に便利・優秀なツールです。ぜひ使いこなせるようにしておきましょう。
加法定理でsin135度とcos135度を求める方法
三角関数では加法定理という公式が登場します。
※加法定理をまだ習っていない人はスキップしていただいて問題ありません。
加法定理とは以下の公式のことです。
※本記事で使用する加法定理のみをピックアップします。
- sin(α+β)=sinαcosβ+cosαsinβ
- cos(α+β)=cosαcosβ-sinαsinβ
加法定理を使ってsin135度とcos135度を求めることも可能です。
135度=45度+90度なので、加法定理より
sin135度=sin(45度+90度)=sin45度・cos90度+cos45度・sin90度=1/√2・0+1/√2・1=1/√2となります。
※sin45度の求め方について解説した記事やsin90度の求め方について解説した記事もぜひ合わせてご覧ください。
また、
cos135度=cos(45度+90度)=cos45度・cos90度-sin45度・sin90度=1/√2・0-1/√2・1=-1/√2となります。
sin135度もcos135度も先ほど単位円を使って求めた値と一致していることが確認できます。
加法定理も非常に便利な公式なので、単位円と同様に必ず使えるようにしておきましょう。
sin135度、cos135度からtan135度を求める
sin135度とcos135度を求めることができたので、ついでにtan135度も求めておきましょう。
tan135度を求めるには三角比の関係式・相互関係の公式tanθ=sinθ/cosθを活用します。
※tanθ=sinθ/cosθがわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
tan135度=sin135度/cos135度=1/√2 ÷ (-1/√2)=-1となります。
三角比においてはsinθ、cosθ、tanθのどれか1つでも値がわかると、残り2つの三角比の値も必ずわかるということを覚えておきましょう。
今回はsin135度とcos135度の求め方について解説しました。単位円と加法定理は両方とも重要なので、どちらでも求められるようにしておきましょう。
慣れてくると加法定理よりも単位円を使った方が早く三角比の値を求めるができるかと思います。