中学数ではxy座標という言葉が登場してきます。後ほど詳しく解説しますが、xy座標とはx軸とy軸が存在する座標のことです。
xy座標とは何かを理解しておかないと、この先の中学数学は必ずつまずいてしまいますので、今のうちにしっかりと理解しておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者がxy座標とは何かについて図解でわかりやすく解説していきます。
また、座標軸や原点などxy座標と一緒に覚えておくべき用語もご紹介していきますので、ぜひ最後までご覧ください。
xy座標とは?
では早速、xy座標とは何かについて解説していきます。
例えば、x=5のときy=3であるとします。これは以下の図ように点Pで表現することができます(このような表し方を座標といいます)
※今回はPという文字を使いましたが、P以外の文字を使っても問題ありません。
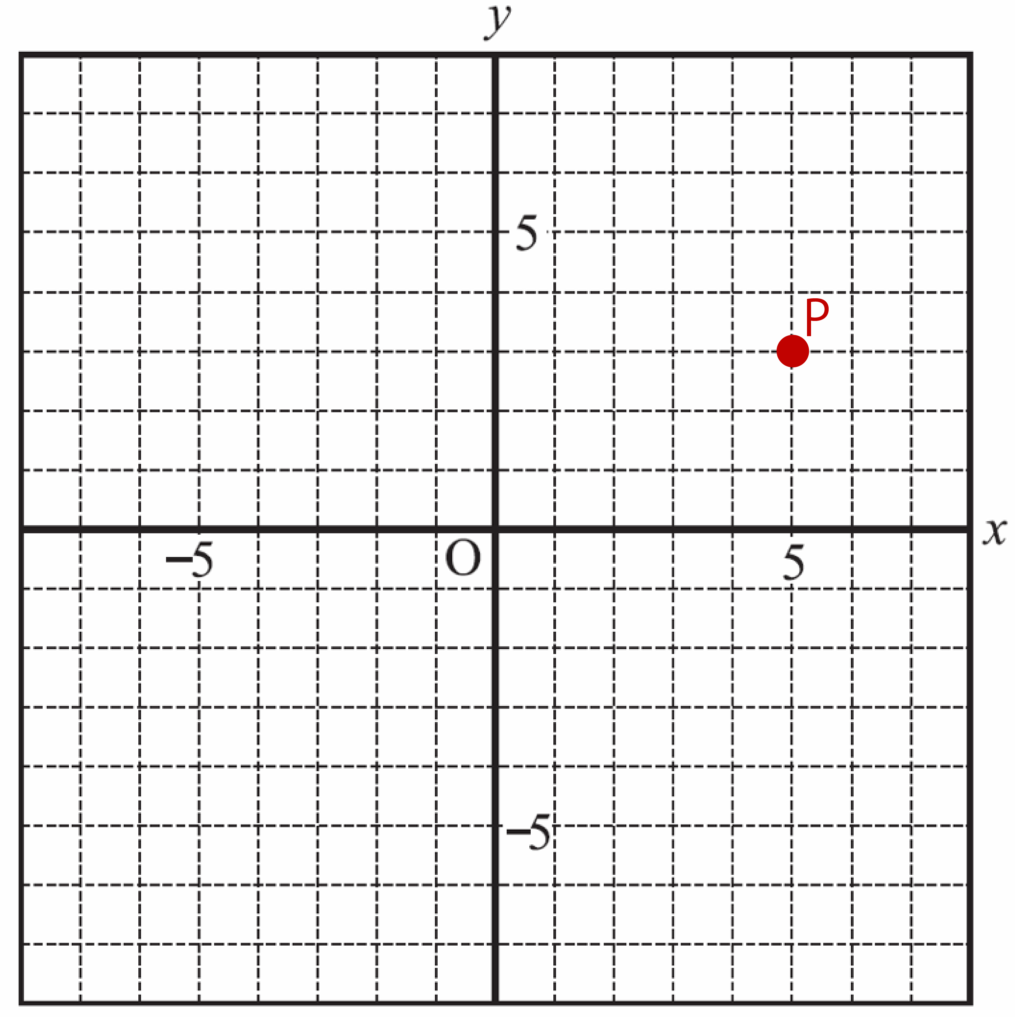
上記の図において、横の直線をx軸、縦の直線をy軸といいます。
特に、x軸とy軸が引いてある座標のことをxy座標といいます。また、x軸とy軸を合わせて座標軸といいます。
さらに、座標軸の交点Oのことを原点といいます。
そして、今回の点Pで示した箇所はx=5、y=3にあたる点ですが、これをP(5、3)と表現します。
5は点Pのx座標、3は点Pのy座標といいます。(5、3)は点Pの座標といいます。
xy座標においてマス目がない場合は?
先ほどご紹介したxy座標では目盛りやマス目がしっかりと記載されていました。
しかし、自分でゼロからxy座標を書いて点P(5、3)の位置を示す場合、いちいちマス目は書いてられません。
そのような場合は以下のようにxy座標を書いて点Pを示しても問題ありません。
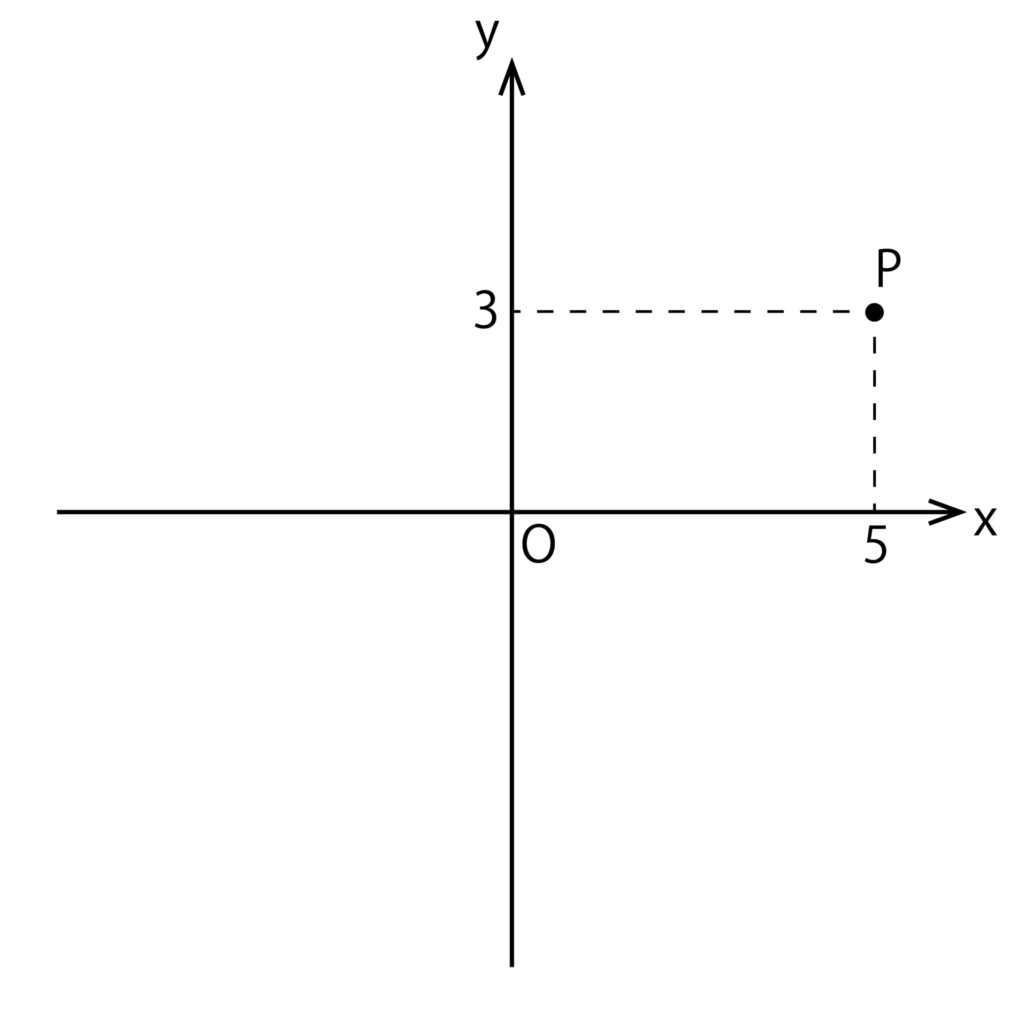
x軸を示すxの表記、y軸を示すyの表記、原点Oの3つは必ず記載しましょう。
xy座標に慣れよう!練習問題
xy座標とは何かについて理解した上で、xy座標に慣れるためにも以下の練習問題を解いてみましょう。
【練習問題1】
以下のxy座標において、点A〜Eの座標を答えなさい。
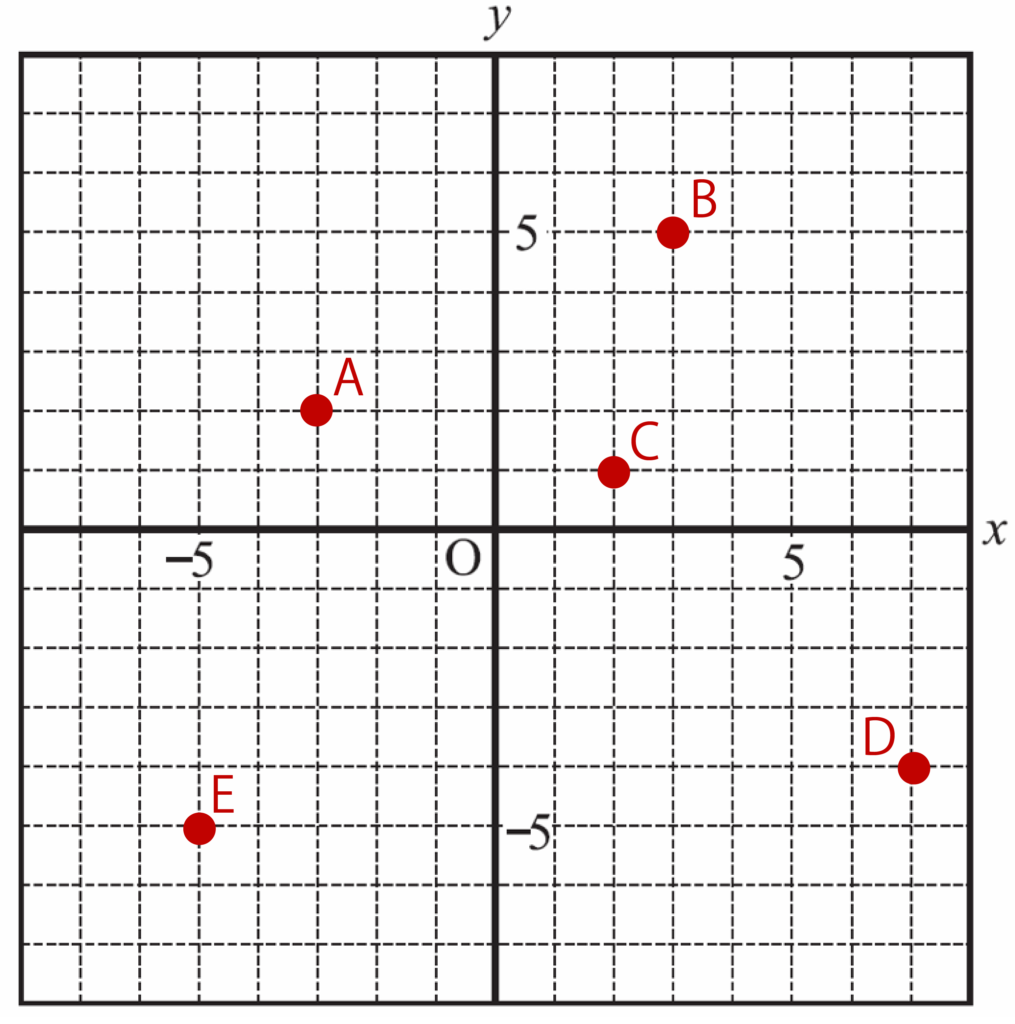
【解答&解説】
上記でも解説した通り、例えばx=5、y=3は(5、3)と示すのでした。x座標→y座標の順番に気をつけてください。
A(-3、2)、B(3、5)、C(2、1)、D(7、-4)、E(-5、-5)となります。
【練習問題2】
以下のxy座標においてP(1、6)、Q(-3、4)、R(6、-2)の位置を示しなさい。
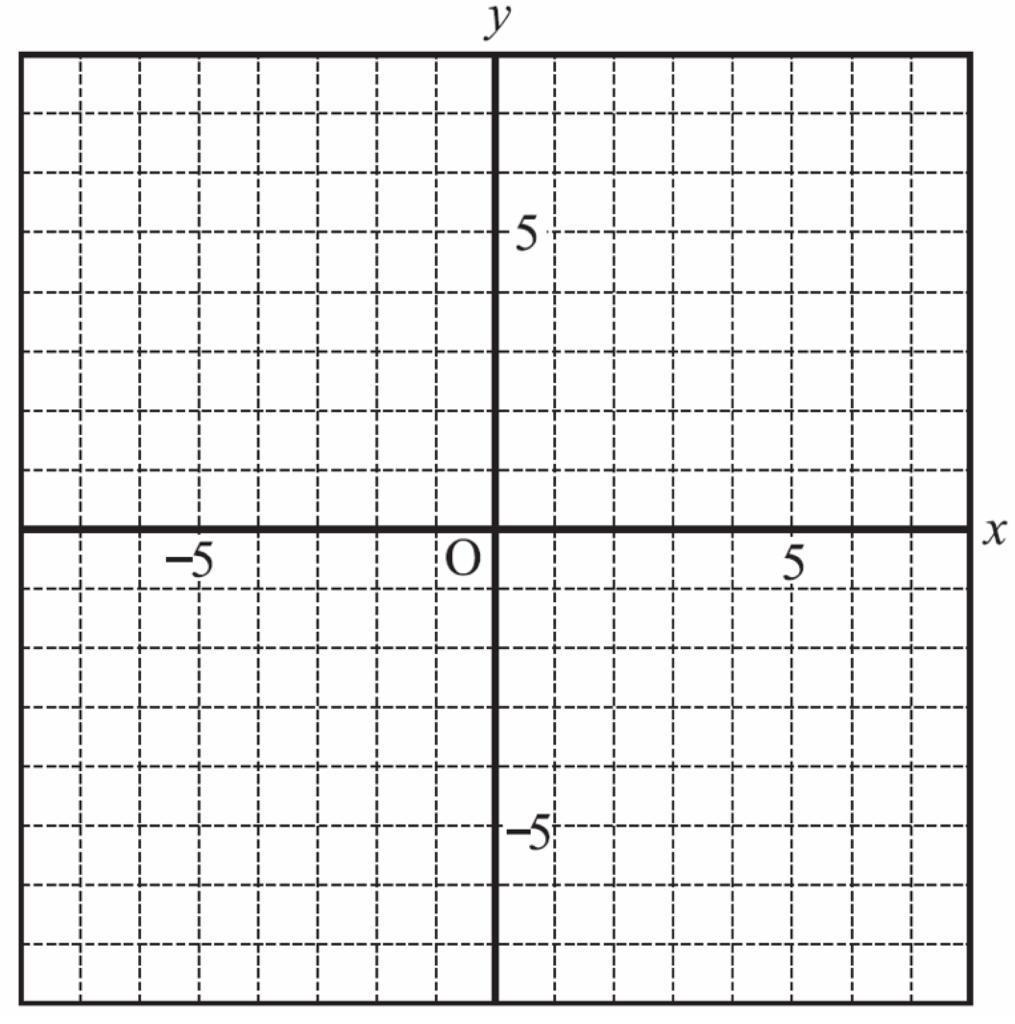
【解答&解説】
以下のようになります。
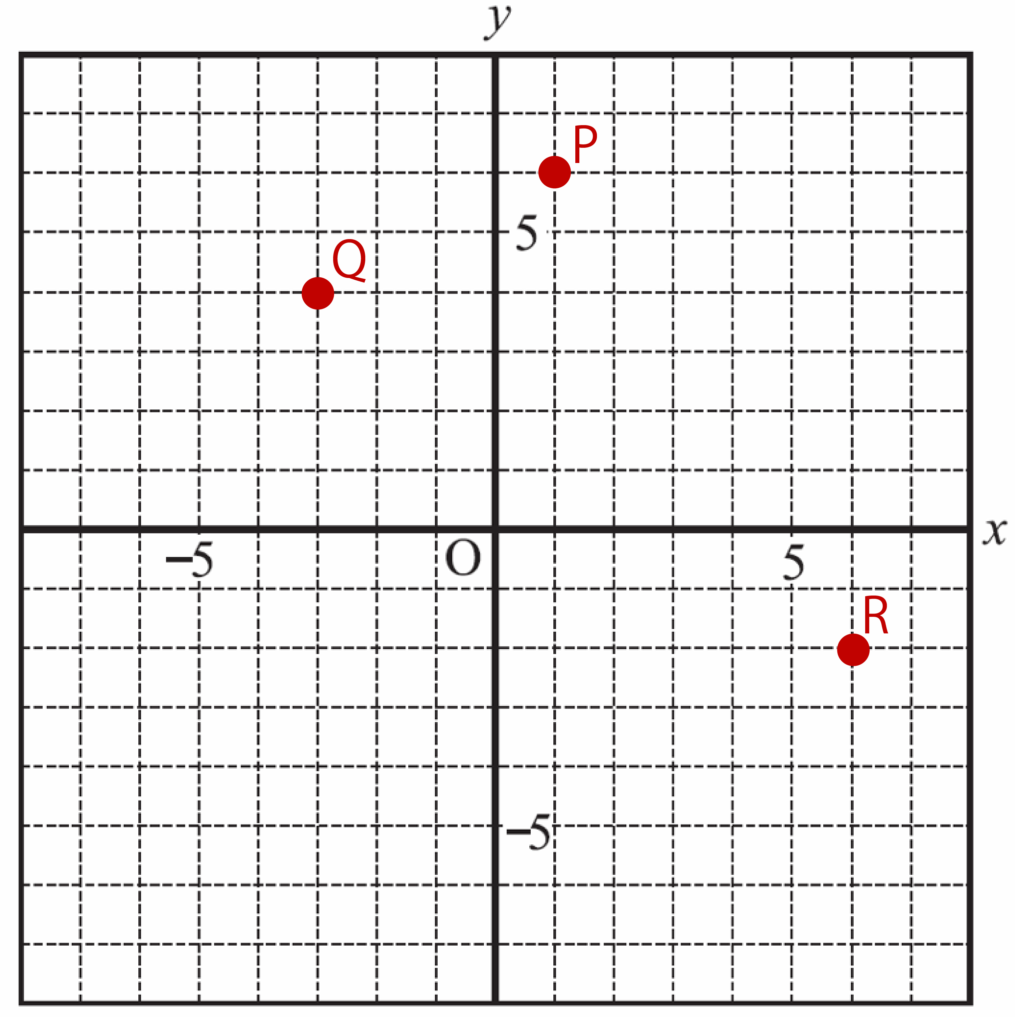
xy座標と象限
xy座標はx軸とy軸によって4つの部分に切り分けられていますが、以下のように各切り分けられた箇所は第1象限、第2象限、第3象限、第4象限と呼ばれています。
x座標、y座標の符号でどの象限かを判断します。
例えば、第1象限はx座標・y座標ともにプラス(+)です。第2象限はx座標はプラス(+)ですが、y座標はマイナス(-)です。
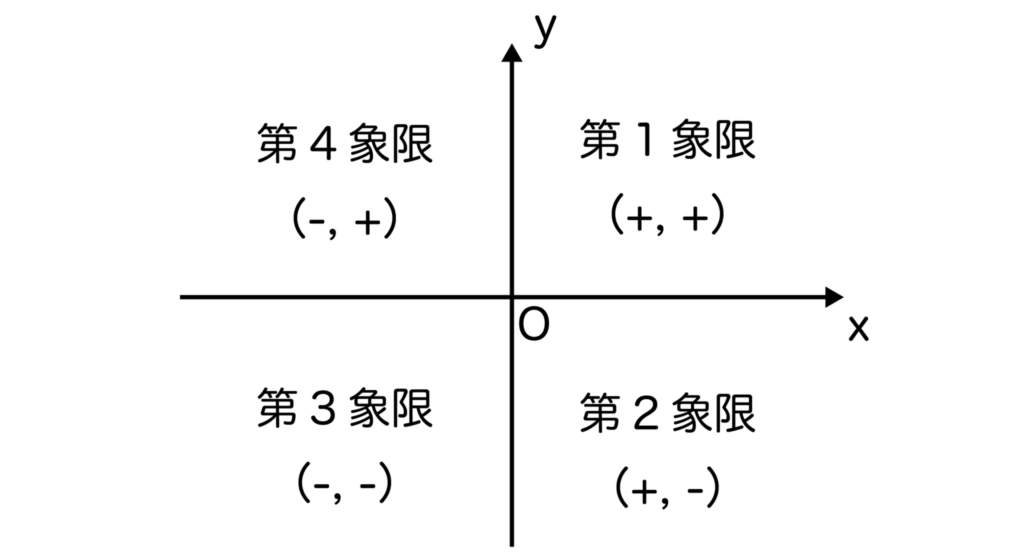
第1象限から反時計まわりに第2象限、第3象限、第4象限となるので、覚えておきましょう。
xy座標における点と点との距離
最後に、xy座標における点と点との距離の求め方について解説して起きます。
以下のように、xy座標においてP(5、3)とQ(3、4)があるとします。
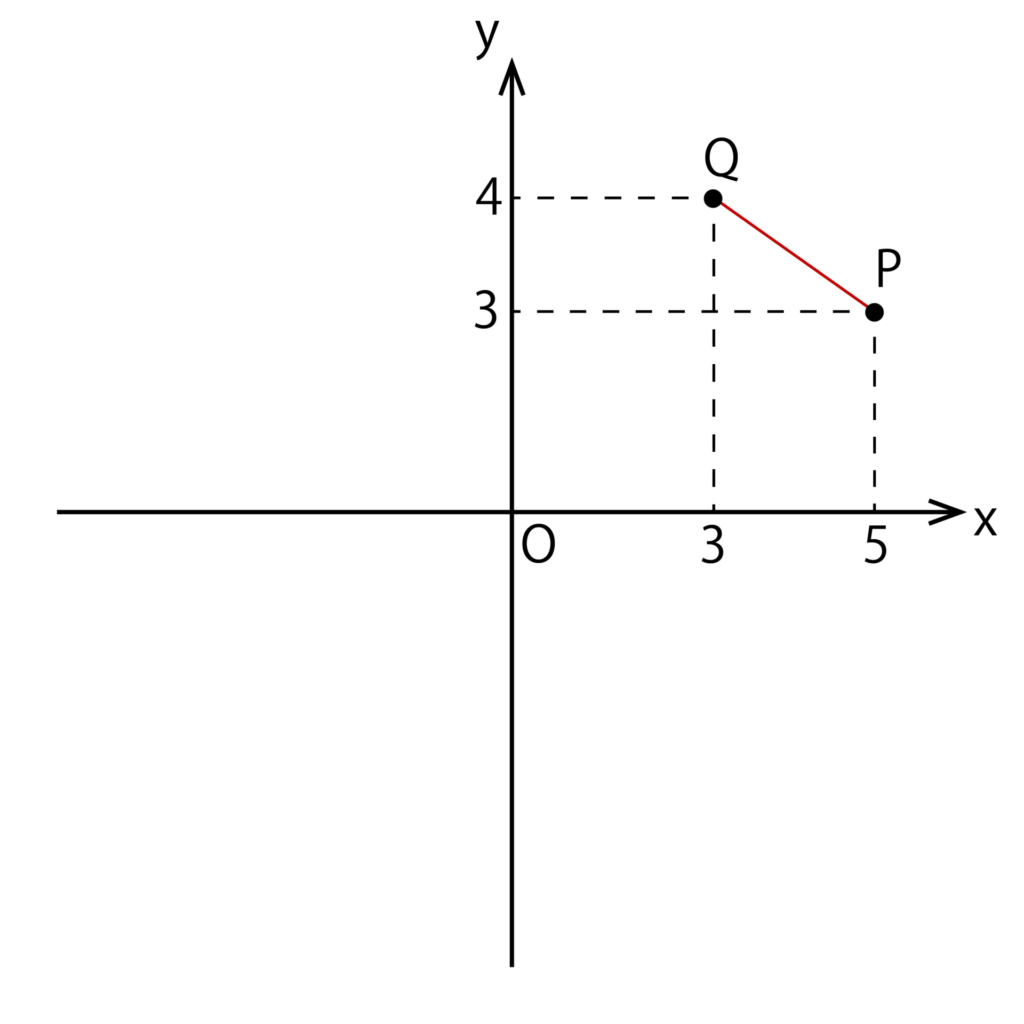
このとき、PQの長さ(距離)を求めてみます。
まず、点Pからy軸に対して下ろした垂線と点Qからx軸に対して下ろした垂線の交点を以下のようにRとしましょう。
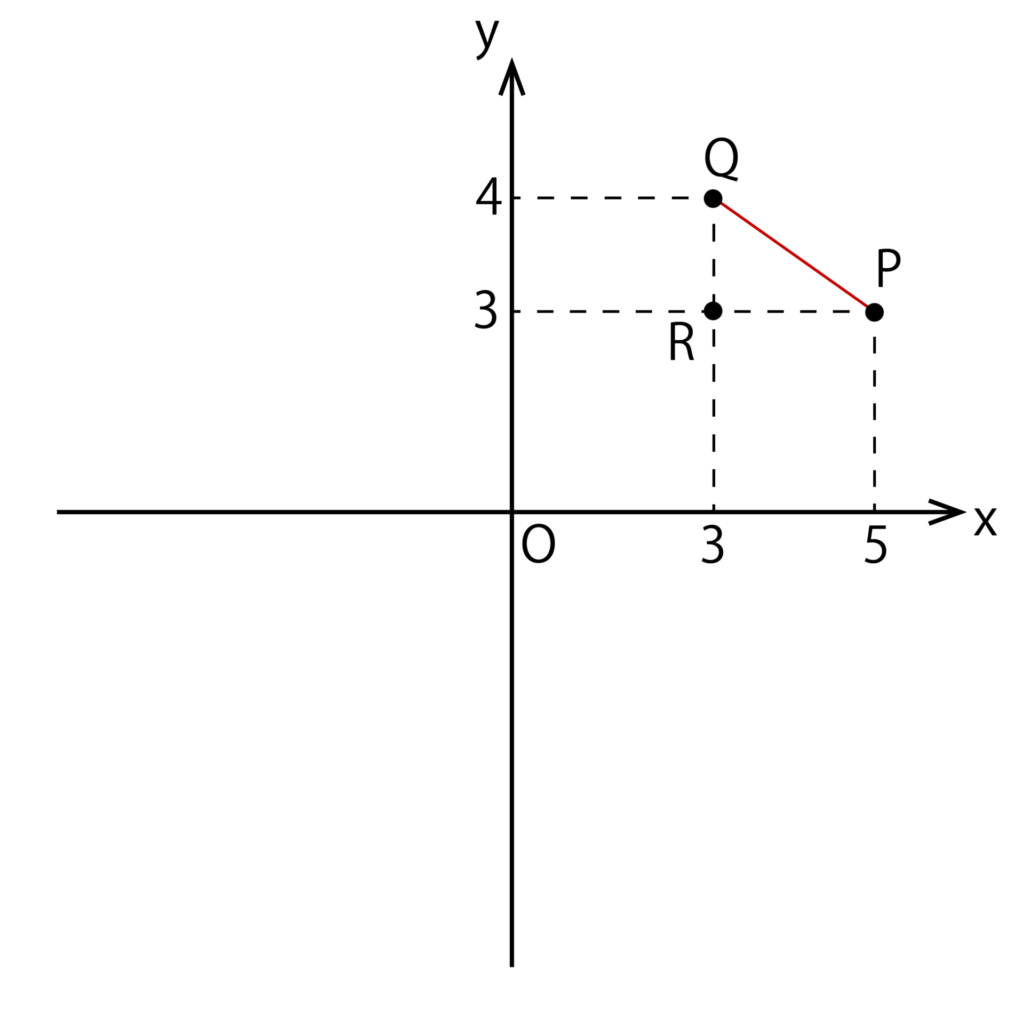
すると、三角形PQRは直角三角形であり、
- PR=Pのx座標-Qのx座標=5-3=2
- QR=Qのy座標-Pのy座標=4-3=1
ですね。よって、三平方の定理よりPQ2=PR2-QR2=22-12=3となるので、PQ=√3となります。
xy座標と三平方の定理は非常に相性が良いので、必ず使えるようにしておきましょう。
いかがでしたか?
今回はxy座標とは何かについて図解で解説していきました。xy座標はこの先の数学でも必ず登場します。
いつでも自分で点の位置を書けるようにしておきましょう!