中学数学で多くの人がつまずきやすい分野の1つが比例と反比例です。
比例と反比例は一見難しそうですが、1つ1つ丁寧に学習していけば難しくはないのでご安心ください。
今回は早稲田大学教育学部数学科を卒業した筆者が比例とは何かについて解説した後、比例の式や比例のグラフの書き方・反比例との違いなど比例に関して必ず知っておくべき知識をわかりやすく解説していきます。
数学が苦手な人でも理解できるようにわかりやすく解説していくので、ぜひ最後までご覧ください。
比例とは?わかりやすく解説
では早速、比例とは何かについて解説していきます。
比例とは変数xとyがあったとき、xの値が2倍、3倍、4倍・・・になるにつれてyの値も2倍、3倍、4倍・・・になることです。
※変数がわからない人は変数とは何かについて解説した記事をご覧ください。
このとき、yはxに比例するといいます。
例えば、y=3xという式があったとしましょう。
すると、
- x=1のときy=3
- x=2のときy=6
- x=6のときy=18
ですね。xの値が1から2になったとき、つまりxの値が2倍になったとき、yの値は3から6に変化しておりyの値も2倍になっていることがわかります。
また、xの値が2から6になったとき、つまりxの値が3倍になったとき、yの値は6から18に変化しておりyの値も3倍になっていることがわかります。
よって、y=3xという式はxはyに比例するといえます。
以上が比例とは何かについての解説となります。
比例の式とは?わかりやすく解説
ここからは比例はどんな式で表現することができるのかについて解説していきます。
結論からいうと、xがyに比例するとき、比例の式はy=axで表現することができます。
先ほどy=3xを例に比例とは何かについて解説しましたが、y=3xも比例の式の1つとなります。
y=3xの場合、a=3です。
その他の比例の式としてはy=5xやy=100x、y=-4x、y=4/7xなどあげればキリがありません。
aは正の数・負の数でも分数でも少数でも問題ありません。ただし、aは0ではないものとします。
※正の数・負の数とは何かについて解説した記事もぜひ合わせてご覧ください。
比例定数とは?求め方は?
先ほど、比例の式はy=axで表現できると解説しましたが、このaのことを比例定数といいます。
例えばy=6xという比例の式があったとき「比例定数を求めよ」といわれたら6が答えとなります。
比例定数はy÷xで求めることができます。比例の式y=axよりa=y/xとなるからです。
では、以下の例題を解いてみましょう。
【例題】
yはxに比例しx=6のとき、y=42である。このとき、比例定数を求めよ。
【解答&解説】
比例定数=y/x=42/6=7となります。
丁寧に解説すると、yはxに比例するので、y=axと表すことができます。x=6のとき、y=42なので、x=6のとき、y=42をy=axに代入すると、42=6aとなりますね。
※6a=6×aのことでした。詳しくは文字と式について解説した記事をご覧ください。
よってa=42/6=7となります。
比例定数は比例の分野の中でも重要な用語の1つなので、必ず覚えておきましょう。比例定数について詳しく解説した記事もぜひ参考にしてください。
比例と反比例の違いをわかりやすく解説
ここからは比例と反比例の違いについて解説します。
先ほど、比例とは変数xとyがあったとき、xの値が2倍、3倍、4倍・・・になるにつれてyの値も2倍、3倍、4倍・・・になることであると解説しました。
それに対して反比例とは、変数xとyがあったとき、xの値が2倍、3倍、4倍・・・になるにつれてyの値も1/2倍、1/3倍、1/4倍・・・になることです。
比例の反対=反比例という理解で問題ありません。
反比例の式はy=a/xとなります(ただし、aは0ではないものとする)
例えば、y=10/xという反比例の式を考えてみると、
- x=2のときy=5
- x=10のときy=1
ですね。xの値が2から10になったとき(5倍になったとき)、yの値は5から1になっているので1/5倍になっていることがわかります。
反比例も比例と同じく非常に重要な分野なので必ず合わせて学習しておきましょう。反比例とは何かについて詳しく解説した記事もご用意しているので、ぜひご覧ください。
比例のグラフと書き方をわかりやすく解説
比例のグラフの書き方は簡単です。
比例のグラフ(y=ax)はxy座標上において必ず原点O(0、0)を通る直線となります。
※xy座標がわからない人はxy座標とは何かについて解説した記事をご覧ください。
例えば、y=3xのグラフは以下のようになります。
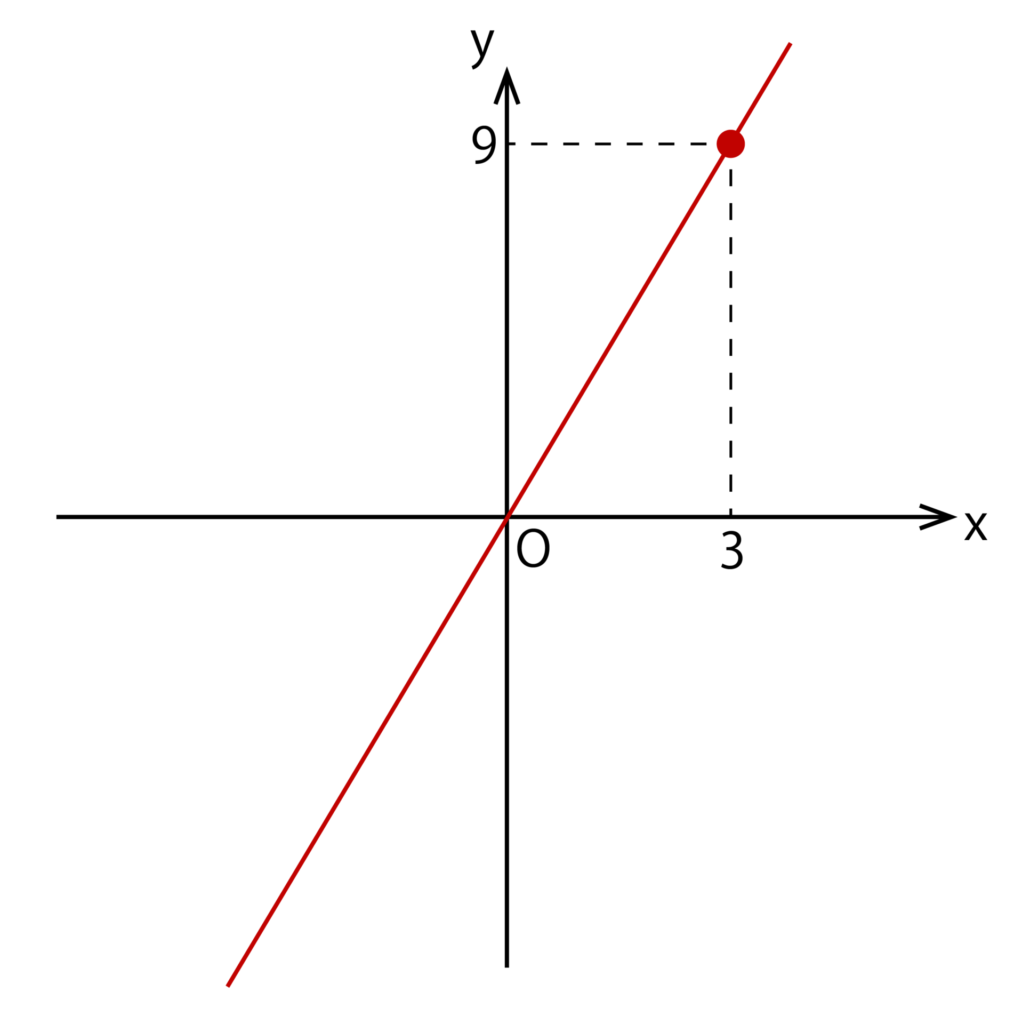
y=3xなので、x=3のときy=9であることがわかります。また、グラフの通り確かに原点Oも通っていることが確認できます。
比例のグラフの特徴としては以下の3つがあります。
- 比例のグラフは必ず直線になる
- 比例のグラフは必ず原点Oを通る
- 比例定数が大きいほどグラフの傾きは急になる
比例のグラフの書き方や特徴について詳しく解説した記事もご用意しているので、ぜひ合わせてご覧ください。
比例の記号をご紹介
比例を表す記号として「∝」があります。「∼」を使うこともあります。
※このパートは数学の教科書では登場しないので、興味がある人だけご覧ください。
例えば「yはxに比例する」を記号「∝」を使って表現する場合、「y∝x」と書きます。
比例の記号「∝」に読み方はなく、「y∝x」と書かれていた場合「yはxに比例する」と読むのが一般的です。
比例と変域について
比例の学習を進めていくと比例と変域が絡んだ問題に遭遇することがあります。
変域とは変化する領域という意味で、xやyの値が制限されることをいいます。
変域は不等号を使って表現されます。例えば、5≦x≦10という変域が与えられた場合、xは5以上10以下の値しか取ることができません。
※不等号がわからない人は不等号の意味や読み方について解説した記事をご覧ください。
比例と変域が絡んだ問題として以下を解いてみましょう。
【問題】
以下の図のようにAB=8cm、AD=10cmの長方形ABCDがある。点PがBC上を点Bから点Cまで1cm/秒の速さで動く。点Pが点Cに到着した後は点Pは動かないものとする。
点Pが点Bを出発してからx秒後の三角形ABPの面積をy[cm2]として以下の問いに答えなさい。
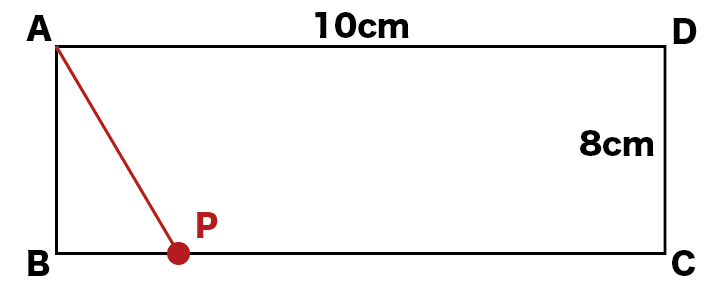
(1)xの変域を求めなさい。
(2)yをxの式で表しなさい。
(3)三角形ABPの面積が20cm2となるのは点Pが点Bを出発してから何秒後か求めなさい。
【解答&解説】
(1)点Pが点Bを出発してから点Cに到着するまでの時間は10÷1=10秒ですね。
よってxの変域は0≦x≦10・・・(答)となります。
(2)三角形ABPの面積y=BP×8÷2で求められますね。
BP=xなので、y=x × 8÷2=4x・・・(答)となります。
(3)y=4xにy=20を代入してx=5となるので、5秒後・・・(答)となります。
一次関数と比例について
中学2年生になると一次関数という分野を学習します。
一次関数は比例とよく似ており、y=ax+bという式で表すことができます。
これは比例の式y=axをy軸方向に+bだけ移動させたものとなります。
例えば一次関数y=x+2のグラフは以下のようになります。
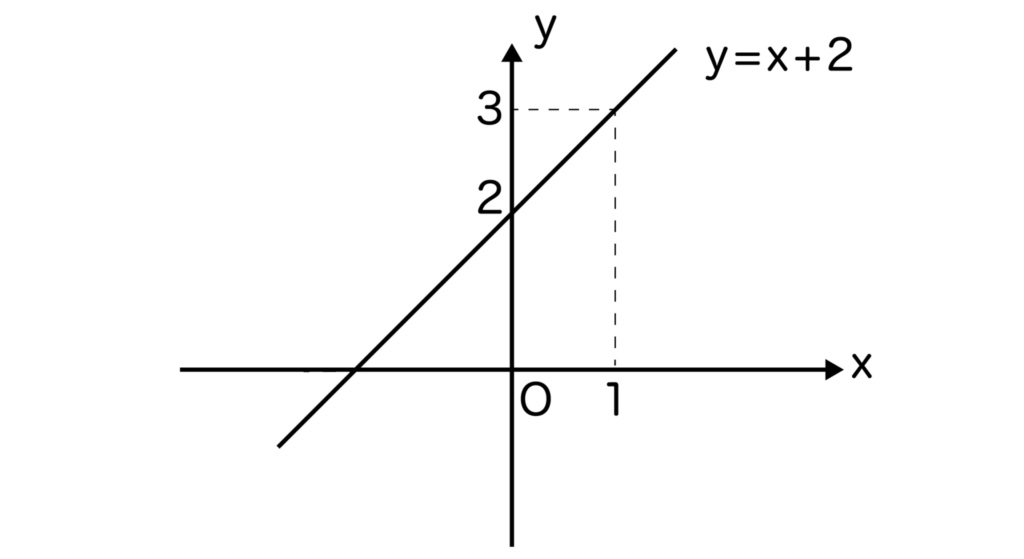
x=1のときy=1+2=3となっていることが確認できます。また、x=0のときy=0+2=2になっていることも確認できます。
一次関数を理解するには比例を理解しておかなければならないので、中学1年生の人はこの先の一次関数でつまずかないためにも、今のうちにしっかりと比例を学習しておきましょう。
一次関数とは何かについて詳しく解説した記事もご用意しているので、興味がある人はぜひご覧ください。
比例を利用した練習問題
最後に比例を利用した練習問題を解いてみましょう。
基礎的な問題なので、比例がしっかり頭に入っていれば問題なく解けるでしょう。
【問題】
60[m/分]で歩くA君がx[分間]で進む距離をy[m]とする。このとき、以下の問いに答えなさい。
(1)yをxの式で表しなさい。
(2)A君が1200m進むのにかかる時間を求めなさい。
【解答&解説】
(1)道のり=速さ×時間で求めることができるのでした。
よってy=60x・・・(答)となります。
(2)y=60xに1200を代入すると、1200=60xとなるのでx=20[分]・・・(答)となります。
いかがでしたか?
今回は比例とは何か・比例の式・グラフの書き方・反比例との違いなどについて解説していきました。
比例は中学数学の重要分野の1つです。高校入試でも頻出なので、必ず理解しておきましょう。


