対頂角・同位角・錯角とは何かについては中学数学で学習しましたが、高校数学の数学Aの教科書でも中学数学の復習として対頂角・同位角・錯角が簡単に取り上げられているケースが多いです。
なので、本記事でも対頂角・同位角・錯角とは何かについて念のため取り上げておきます。
今回は早稲田大学教育学部数学科を卒業した筆者が対頂角・同位角・錯角とは何かについて解説した後、対頂角・同位角・錯角が等しい理由(証明)について図解で解説していきます。
数学が苦手な人でも理解できようにわかりやすく解説していくので、ぜひご覧ください。
対頂角・同位角・錯角とは?
まずは対頂角・同位角・錯角とは何かについて図解で解説していきます。
まずは対頂角からです。
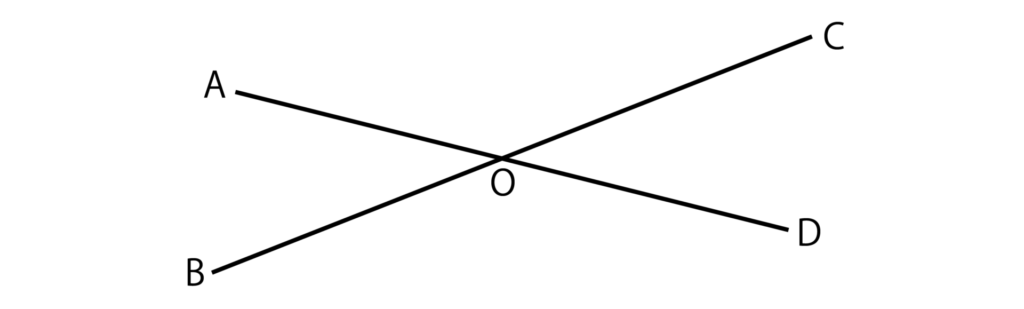
対頂角とは以下のような2直線があったときに向かい合う角のことです。
∠AOBの対頂角は∠CODとなり、∠AOCの対頂角は∠BODとなります。
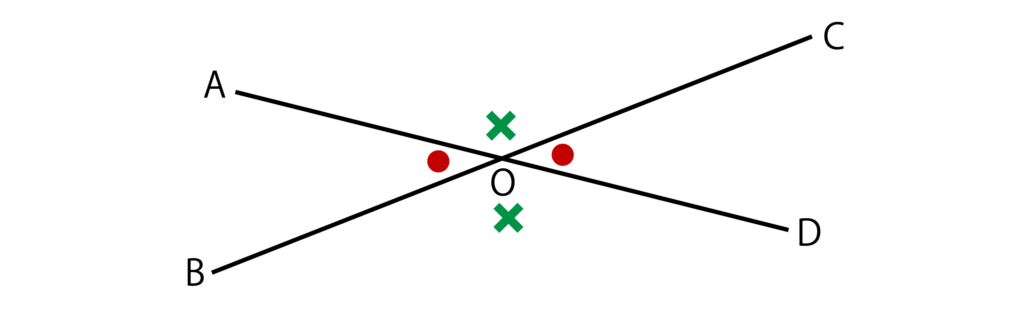
そして、対頂角は等しいという性質があります。
つまり、∠AOB=∠COD、∠AOC=∠BODが成り立ちます。
以上が対頂角とは何かについての解説となります。
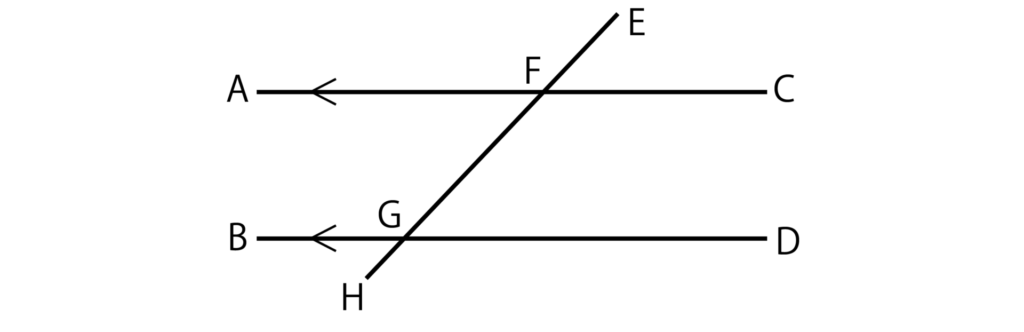
続いては同意角です。以下の図のようにAB//CDなとき、∠EFCの同意角は∠FGDとなります。
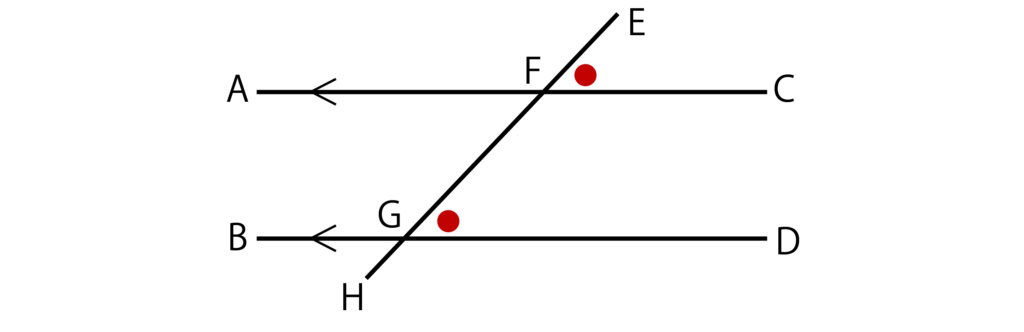
そして、同意角は等しいという性質があります。つまり、∠EFC=∠FGDが成り立ちます。
以上が同意角とは何かについての解説となります。
最後は錯角とは何かです。以下の図のようにAB//CDなとき、∠GFAの錯角は∠FGDとなります。

錯角は等しいという性質があります。つまり、∠GFA=∠FGDが成り立ちます。
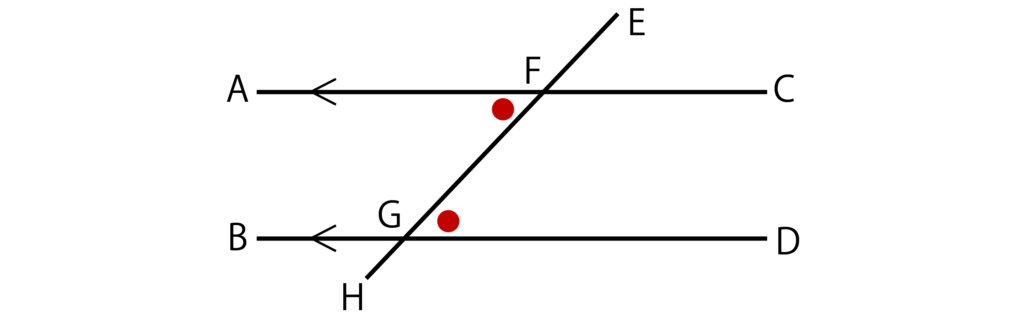
以上が錯角とは何かについての解説となります。
以上で解説した対頂角・同位角・錯角はすべて中学数学で学習する内容です。非常に基礎的な内容なので必ず理解しておきましょう。
対頂角が等しい理由の証明
ここからは対頂角が等しい理由を証明していきます。
以下の図において∠AOBと∠CODは対頂角なので、∠AOB=∠CODとなります。
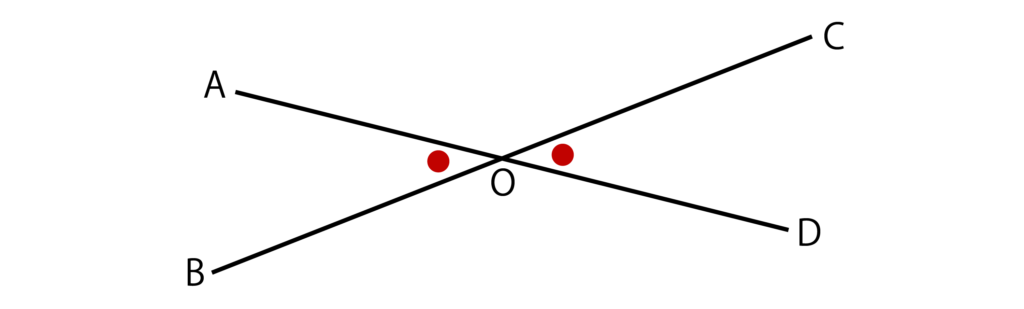
∠AOB=∠CODを証明していきます。
【証明】
BCは直線なので、∠AOB+∠AOC=180度・・・①ですね。
また、ADも直線なので∠AOC+∠COD=180度・・・②です。
①-②より、∠AOB-∠COD=0となるので、∠AOB=∠CODが証明できます。
簡単でしたね。
以上では対頂角が等しい証明を行いまいしたが、数学の問題を解くにあたっては「対頂角は等しい」は証明なしで使って問題ありません。
同位角が等しい理由の証明
次は同意角が等しい理由を証明していきます。
以下の図において∠EFCと∠FGDは同意角なので、∠EFC=∠FGDとなります。

では、∠EFC=∠FGDを証明していきましょう。
【証明】
とは言いつつも、同意角が等しいことをしっかり数学的に証明しようとすると大学数学もしくはそれ以上の領域に突入してしまいます。
なので、本記事では中学生・高校生向けの簡易的な証明を記載することとします。
まず、以下のようにACとBDに垂直に交わるように線を引きます(以下の図における赤線)
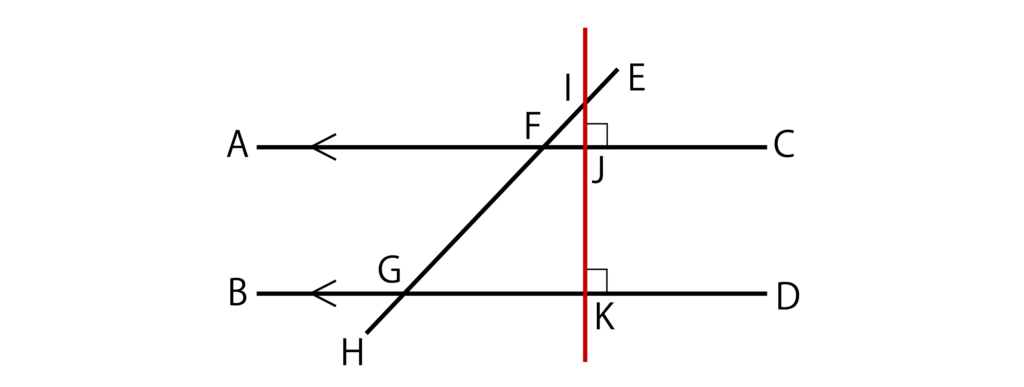
そして、三角形IFJと三角形IGKに注目します。
すると、∠FIJ=∠GIK、∠IJF=∠IKG=90度なので、三角形IFJと三角形IGKは相似であることがわかります。
よって∠EFC=∠FGDが成り立つことが証明できました。
「同意角は等しい」というのも、数学の問題を解くときは証明なしに使って問題ありません。
錯角が等しい理由の証明
最後は錯角が等しい理由の証明を行います。
以下の図において∠AFGと∠FGDは錯角なので、∠AFG=∠FGDとなります。

では、∠AFG=∠FGDであることを証明していきます。
【証明】
上記で対頂角は等しいことの証明を行いました。
よって、∠AFG=∠EFC・・・①となります。
また、上記で同意角は等しいことの証明も行いました。
よって、∠EFC=∠FGD・・・②となります。
①・②より。∠AFG=∠FGDが証明できました。
錯角の証明は対頂角と同意角を使えば簡単に行うことができます。
「錯角は等しい」に関しても、数学の問題では証明なしに使って問題ありません。
対頂角・同位角・錯角の練習問題
では最後に、対頂角・同位角・錯角の練習問題を解いてみましょう。
超基本問題となりますので、必ず解けるようにしておきましょう。
【問題】
以下の図において、∠BOGと∠FEDの大きさを求めよ。
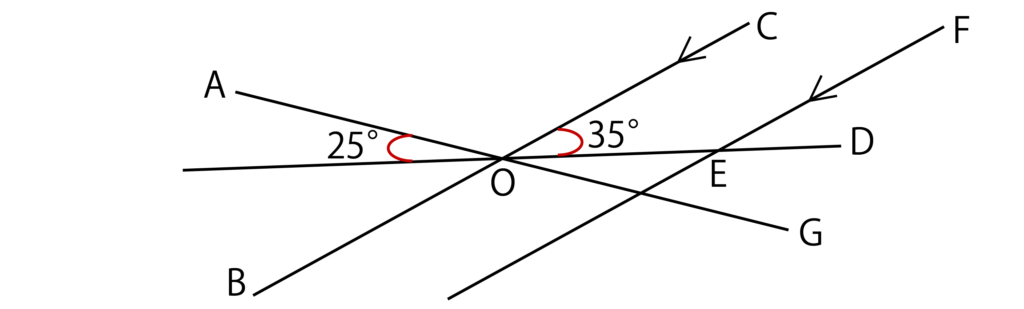
【解答&解説】
∠AOC=180°-25°-35°=120°ですね。
∠BOGと∠AOCは対頂角なので、∠BOG=∠AOCとなります。よって、∠BOG=120°・・・(答)となります。
また、CB//FEより、同意角は等しいから∠FED=∠CODです。
よって、∠FED=35°・・・(答)となります。
いかがでしたでしょうか?
今回は対頂角・同位角・錯角とは何かについて解説しました。
繰り返しにはなりますが、対頂角・同位角・錯角が等しいことは証明なしに使って問題ありません。対頂角・同位角・錯角は図形問題の基本となりますので、必ず理解しておきましょう。


