二次関数では頂点・軸という用語が登場します。
二次関数の頂点・軸とは何かを理解していないと、この先、二次関数の問題を解くことができません。必須の知識なので本記事で必ず覚えましょう。
今回は早稲田大学教育学部数学科を卒業した筆者が二次関数の頂点・軸とは何かについて解説した後、頂点を求めるための公式や平行移動との関係なども解説していきます。
二次関数の頂点・軸に関して必要な情報は本記事を読めばマスターできるので、ぜひ最後までお読みください。
二次関数の頂点・軸とは?
まずは二次関数の頂点・軸とは何かについて解説します。
まずは二次関数の軸からですが、軸とは二次関数のグラフの対称軸のことを指しています。
二次関数のグラフは必ず放物線状になっており、1本の縦のまっすぐな線で左右対称にすることができます。
※二次関数のグラフの作成方法を解説した記事もぜひ合わせてご覧ください。
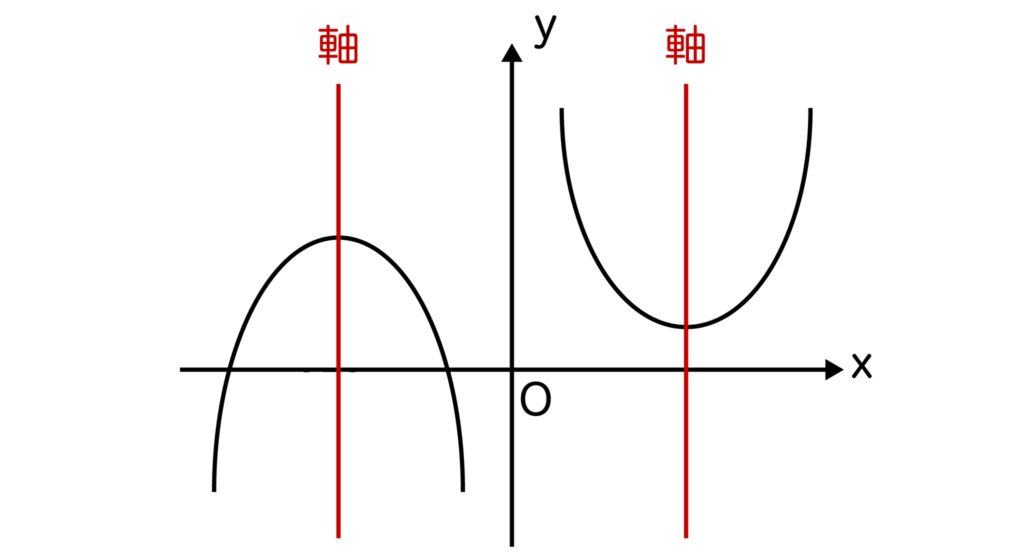
その縦のまっすぐな線のことを軸といいます。軸は縦にまっすぐな直線なのでx=a(aは実数)で表すことができます。
※実数がわからない人は実数とは何かについて解説した記事をご覧ください。
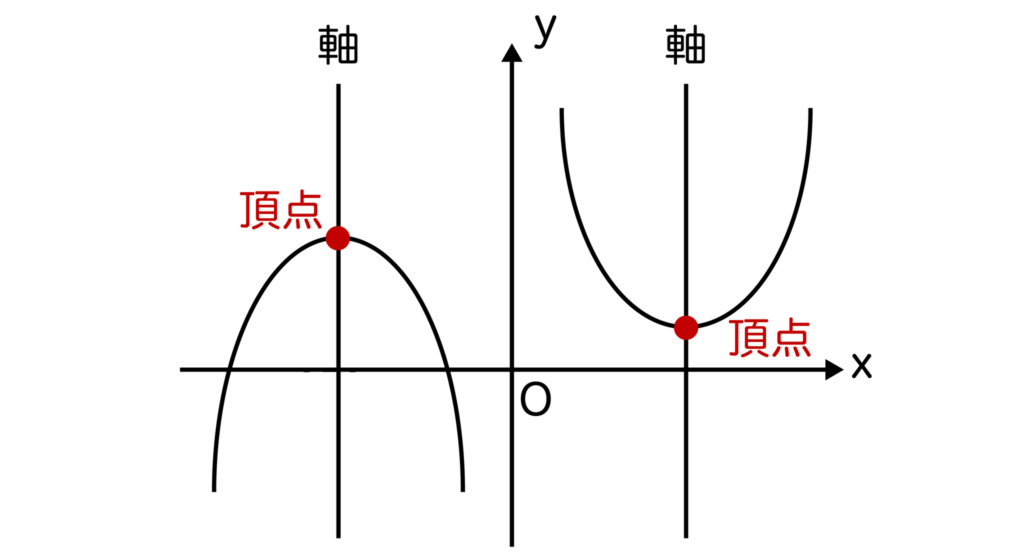
そして、二次関数の頂点とは軸と放物線の交点のことをいいます。
二次関数の頂点と軸を求める方法2つ
ここからは二次関数の頂点と軸を求める方法について解説していきます。
※頂点が求まれば軸は求まります。
二次関数の頂点を求める方法は2つあります。
方法その1:平方完成を使う
y=ax2+bx+cという二次関数があったとき、y=ax2+bx+cを平方完成するとy=a(x-p)2+qになる場合、頂点は(p、q)となります。
例えば、y=x2+8x+10という二次関数があったとします。
y=x2+8x+10を平方完成するとy=(x+4)2-6ですね。
※平方完成のやり方がわからない人は、平方完成の公式・やり方について解説した記事をご覧ください。
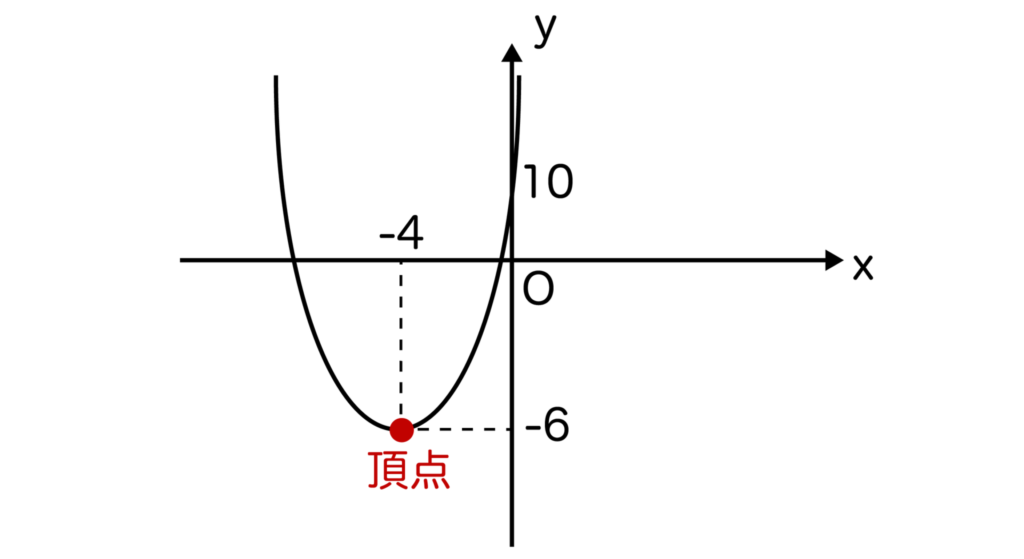
よって、y=x2+8x+10の頂点の座標は(-4、-6)となります。
また、先ほども解説した通り、二次関数の頂点は軸と放物線の交点なので軸はx=-4となります。
方法その2:公式を使う
二次関数y=ax2+bx+cがあるとき、頂点の座標は(-b/2a、-(b2-4ac)/4a)となります。
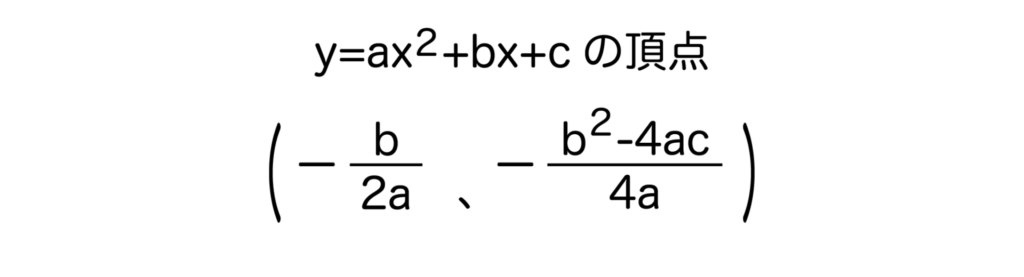
二次関数の頂点を求める公式として覚えておくと便利です。
先ほど二次関数y=x2+8x+10の頂点を平方完成を使って求めましたが、今度は以上の公式を使って頂点を求めてみましょう。
y=x2+8x+10より、a=1、b=8、c=10なので、頂点の座標は
(-8/2×1、-(82-4×1×10)/4×1)
=(-4、-6)
となり、先ほど平方完成を使って求めた頂点の座標と確かに一致しています。
以上の公式で二次関数の頂点が求められることの証明も行なっておきます。
二次関数y=ax2+bx+cを平方完成することを考えましょう。
y=ax2+bx+c
=a(x2+b/a・x)+c
=a(x+b/2a)2-a(b/2a)2+c
=a(x+b/2a)2-a(b2/4a2)+c
=a(x+b/2a)2-(b2/4a)+c
=a(x+b/2a)2+(-(b2-4ac)/4a)
より、頂点の座標が(-b/2a、-(b2-4ac)/4a)となることが確認できました。
二次関数の頂点から式を求める方法
二次関数では、その二次関数が通る2点がわかると、そこから二次関数の式を求めることも可能です。
例えば、頂点(-1、4)と(3、36)を通る二次関数の式を求めてみましょう。
まず、頂点(-1、4)を通るということは、求める二次関数の式は
y=a(x+1)2+4と表すことが可能ですね。
この二次関数が(3、36)を通るので、上記の式にx=3、y=36を代入します。
36=a(3+1)2+4
より、36=16a+4となるのでa=2が求まります。
したがって求める二次関数の式はy=2(x+1)2+4・・・(答)となります。
y=2(x+1)2+4を展開してy=2x2+4x+6としても問題ありませんが、y=a(x-p)2+qの形も綺麗な形なので、わざわざ展開して回答する必要はありません。
※展開のやり方がわからない人は多項式の計算方法について解説した記事をご覧ください。
二次関数の頂点と平行移動
先ほど、二次関数y=a(x-p)2+qのグラフの頂点は(p、q)であると解説しましたが、y=a(x-p)2+qはy=ax2をx軸方向にp、y軸方向にqだけ平行移動したグラフとなります。
※二次関数の平行移動について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
一般的に関数y=f(x)のグラフFをx軸方向にp、y軸方向にqだけ平行移動して得られるグラフGの方程式はy-q=f(x-p)となります。
※y+q=f(x+p)ではないのでご注意ください。
以上が成り立つ証明は以下となります。
Fが放物線y=ax2である場合について考えてみましょう。
G上に任意の点P(x、y)を取り、点Pをx軸方向にp、y軸方向にqだけ平行移動した点をQ(X、Y)とします。
すると、x=X+p、y=Y+qよりX=x-p、Y=y-qとなりますね。
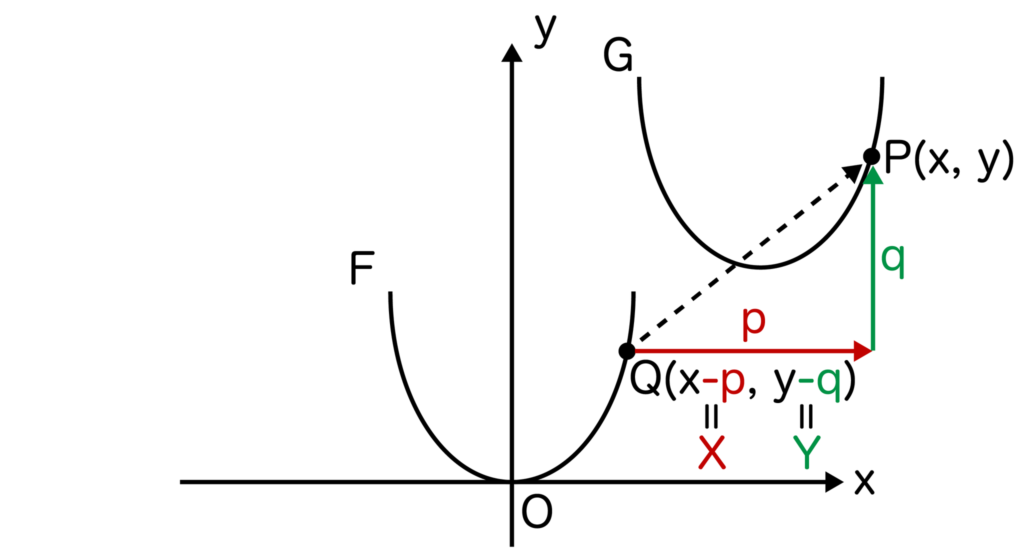
点QはF上にあるのでY=aX2が成り立ちます。
これにX=x-p、Y=y-qを代入すると、Gの方程式は
y-q=a(x-p)2となることがわかります。
二次関数の頂点と軸に関する練習問題
最後に二次関数の頂点と軸に関する練習問題をご用意しました。
どれも基本的な問題なので、すべて解けるようにしておきましょう。
【練習問題1】
以下の二次関数の頂点の座標と軸の式を求めなさい。
(1)y=x2+8x+9
(2)y=-x2-6x+30
(3)y=5x2+8x+21
【解答&解説】
(1)y=x2+8x+9=(x+4)2-7より、頂点は(-4、-7)・・・(答)
軸はx=-4・・・(答)
(2)y=-x2-6x+30=-(x2+6x-30)=-(x+3)2+39より、頂点は(-3、39)・・・(答)
軸はx=-3・・・(答)
(3)平方完成するのが少しめんどくさそうなので、頂点の公式を使いましょう。
頂点は(-8/(2×5)、-(82-4×5×21)/4×5)=(-4/5、89/5)・・・(答)となります。
軸はx=-4/5・・・(答)です。
【練習問題2】
頂点が(4、8)で点(8、40)を通る二次関数の式を求めよ。
【解答&解説】
頂点が(4、8)より求める二次関数の式はy=a(x-4)2+8とおくことができます。
これが(8、40)を通るので40=a(8-4)2+8という方程式が立てられます。
40=16a+8より、a=2となるので求める二次関数の式はy=2(x-4)2+8・・・(答)となります。
【練習問題3】
二次関数y=x2+12x+6のグラフはy=x2のグラフをx軸方向、y軸方向それぞれにどれだけ並行移動させたグラフか答えよ。
【解答&解説】
二次関数y=x2+12x+6を平方完成すると(x+6)2-30となるので、y=x2のグラフをx軸方向に-6、y軸方向に-30だけ平行移動させたグラフとなります。
今回は二次関数の頂点と軸とは何か?、求め方・公式について解説した後、二次関数の頂点から式を求める方法や二次関数の頂点と平行移動の関係についても解説しました。
本記事で解説したことはすべて基本的な内容なので、何度も読み返して必ず頭に入れておきましょう。


