三角比ではsinやcos、tanを用いた関係式(公式)があります。
この関係式は三角比の相互関係とも言われています。
今回は早稲田大学教育学部数学科を卒業した筆者が三角比の関係式・相互関係をご紹介した後、なぜその関係式・相互関係が成り立つのか?の証明も行います。
また、最後には三角比の関係式・相互関係を活用した問題もご用意しています。ぜひ最後までご覧ください。
三角比の関係式・相互関係
では早速、三角比の関係式・相互関係をご紹介します。
まずは以下3つの公式を覚えましょう。
θが鋭角、すなわち0°<θ<90°のとき以下が成り立つ。
- tanθ=sinθ/cosθ
- sin2θ+cos2θ=1
- 1+tan2θ=1/cos2θ
※三角比(sin、cos、tan)がわからない人は三角比の覚え方について解説した記事をご覧ください。
また、90°-θの三角比に関して、以下が成り立ちます。
※こちらもθが鋭角、すなわち0°<θ<90°とします。
- sin(90°-θ)=cosθ
- cos(90°-θ)=sinθ
- tan(90°-θ)=1/tanθ
以上の6つは大学入試や共通テストでもよく登場するので、公式として暗記してしまいましょう。
※ちなみにですがsin90度=1となります。sin90度が1なのはなぜかについて解説した記事もぜひ参考にしてください。
三角比の関係式・相互関係の証明
ここからは、上記でご紹介した三角比の関係式・相互関係がなぜ成り立つのかについて証明を行います。
まずは以下の3つから証明を行います。
- tanθ=sinθ/cosθ
- sin2θ+cos2θ=1
- 1+tan2θ=1/cos2θ
以下の図の直角三角形ABCにおいて、cosθ=x/r、sinθ=y/rですね。
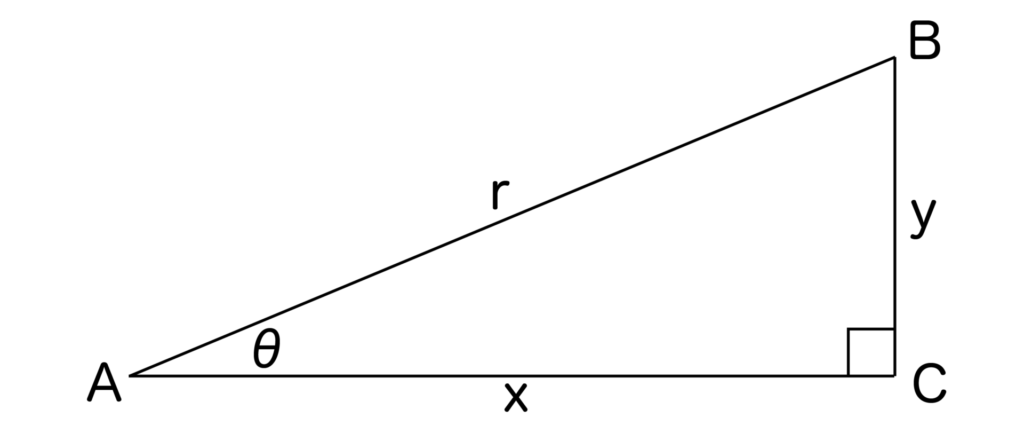
つまり、x=rcosθ、y=rsinθとなります。
よって、tanθ=y/x=rsinθ/rcosθ=sinθ/cosθが証明できました。
また、三平方の定理よりx2+y2=r2が成り立ちます。
したがって、(rcosθ)2+(rsinθ)2=r2
両辺をr2で割って、sin2θ+cos2θ=1が証明できました。
さらに、sin2θ+cos2θ=1の両辺をcos2θで割ると、
tan2θ+1=1/cos2θが証明できました。
※tanθ=sinθ/cosはすでに証明できているので、sin2θ/cos2θ=tan2θとなります。
3つの三角比sinθ、cosθ、tanθのどれか1つでも値がわかると、上記3つの公式を使うことによって残り2つの三角比の値も計算可能になるということを覚えておきましょう。
続いては以下3つの証明です。
- sin(90°-θ)=cosθ
- cos(90°-θ)=sinθ
- tan(90°-θ)=1/tanθ
また以下の図の直角三角形ABCを使います。

以上の図の直角三角形ABCにおいて、∠B=90°-θですね。
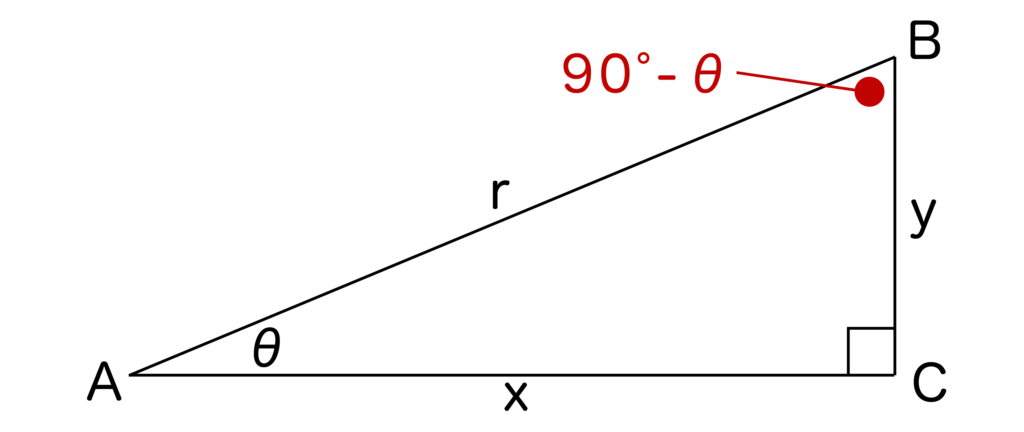
よって、sin(90°-θ)=x/r=cosθ
cos(90°-θ)=y/r=sinθ
tan(90°-θ)=x/y=1/tanθ
が証明できました。
上記3つの関係式を用いると、鋭角の三角比はすべて45°以下の角の三角比で表現することができます。
【例】
- sin66°=sin(90°-24°)=cos24°
- cos76°=cos(90°-14°)=sin14°
- tan50°=tan(90°-40°)=1/tan40°
三角比の関係式・相互関係を使った問題
最後に、三角比の関係式・相互関係を使った問題をご紹介します。
以上でご紹介した6つの三角比の関係式・相互関係をしっかり暗記して解いてみてください。
【問題】
(1)θは鋭角とする。sinθ=3/4のとき、cosθおよびtanθの値を求めよ。
(2)θは鋭角とする。tanθ=3のとき、sinθおよびcosθの値を求めよ。
(3)三角形ABCの3つの内角∠A、∠B、∠Cの大きさをそれぞれA、B、Cとする。このとき、sin(A/2)=cos{(B+C)/2}が成り立つことを証明せよ。
【解答&解説】
(1)三角比の関係式・相互関係のsin2θ+cos2θ=1より、
cos2θ=1-sin2θ=1-(3/4)2=7/16となります。
θは鋭角であることから、cosθ>0となるのでcosθ=√7/4・・・(答)となります。
tanθ=sinθ/cosθ=3/4÷√7/4=3/√7=3√7/7・・・(答)となります。
(2)三角比の関係式・相互関係の1+tan2θ=1/cos2θより、
1/cos2θ=1+32=10となるのでcos2θ=1/10が求まります。
θは鋭角であることから、cosθ>0となるのでcosθ=1/√10・・・(答)となります。
sinθ=tanθ・cosθ=3・1/√10=3/√10=3√10/10・・・(答)となります。
(3)A+B+C=180°より、B+C=180°-Aとなります。
よって、(B+C)/2=(180°-A)/2=90°-A/2となるので、
cos{(B+C)/2}=cos(90°-A/2)=sin(A/2)が成り立つことがわかります。
今回は三角比の関係式・相互関係の解説・証明を行いました。
特にsin2θ+cos2θ=1は大学入試・共通テストでも頻出で特に重要です。利用する場面が多いので必ず覚えておきましょう。


