sinやcosの値は求められるけど、tanの値を求めるのが苦手という人も多いのではないでしょうか?
tanは定義されていない値もあり、sinやcosと比べたら確かに求めにくいかもしれません。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がtan30度の値の求め方を図解で解説します。
数学が苦手・三角関数が苦手な人でも理解できるように解説していくので、ぜひ最後までお読みください。
tan30度の求め方その1
では早速、tan30度を求めていきましょう。
もっとも簡単な方法は自分で図形を書いてtan30度を求める方法です。
以下のように左下が30度の直角三角形ABC(∠ABC=60度)を書いてみましょう。すると、直角三角形ABCは辺の比が1:2:√3の直角三角形であることがわかります。
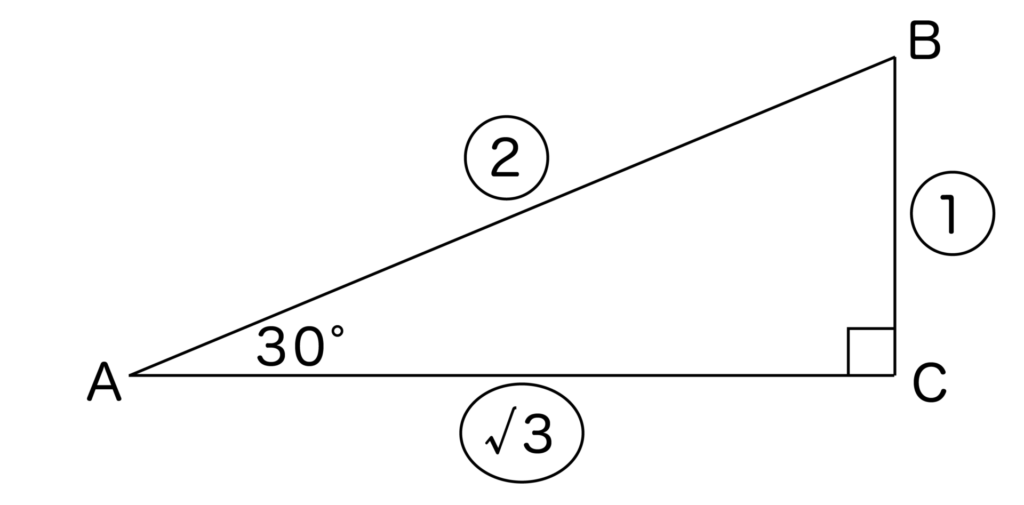
ここで、改めてtanの求め方を復習しておきましょう。
tan30度は上記の図においてBC/ACとなるのでした。
※tan30度がBC/ACになる理由がわからない人は三角比の覚え方について解説した記事をご覧ください。
したがって、tan30度=1/√3となります。
以上が最も簡単なtan30度の求め方です。必ずできるようにしておきましょう。
今回は辺の比を活用してtan30度の値を求めましたが、辺の長さが与えられているときはそれを活用しても問題ありません。
例えば、以下のようにAB=20cm、BC=10cm、AC=10√3cmの直角三角形ABCがあるとします。
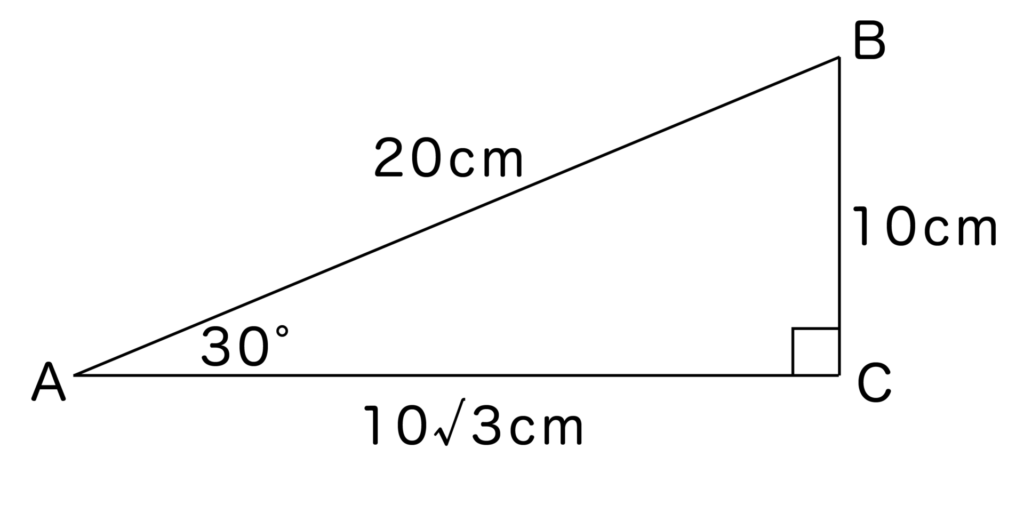
この直角三角形も先ほどと同様に辺の比が1:2:√3の直角三角形ですね。
辺の長さを使ってtan30度を求めると、tan30度=10/10√3=1/√3となります。
先ほど辺の比を活用した求めたtan30度の値と確かに同じになっていますね。辺の長さを活用する場合でも、最終的には約分することになるので筆者のおすすめは辺の比を活用することです。
tan30度の求め方その2
tan30度の求め方2つ目は単位円を活用することです。
単位円とはxy平面において原点Oを中心とした半径=1の円のことでした。三角関数の学習において単位円は非常に重要な役割を果たします。
今回はtan30度の値を求めるので、単位円においてθ=30度を以下のように取りましょう。
そして、点Pからx軸に対して下ろした垂線とx軸との交点をQとします。
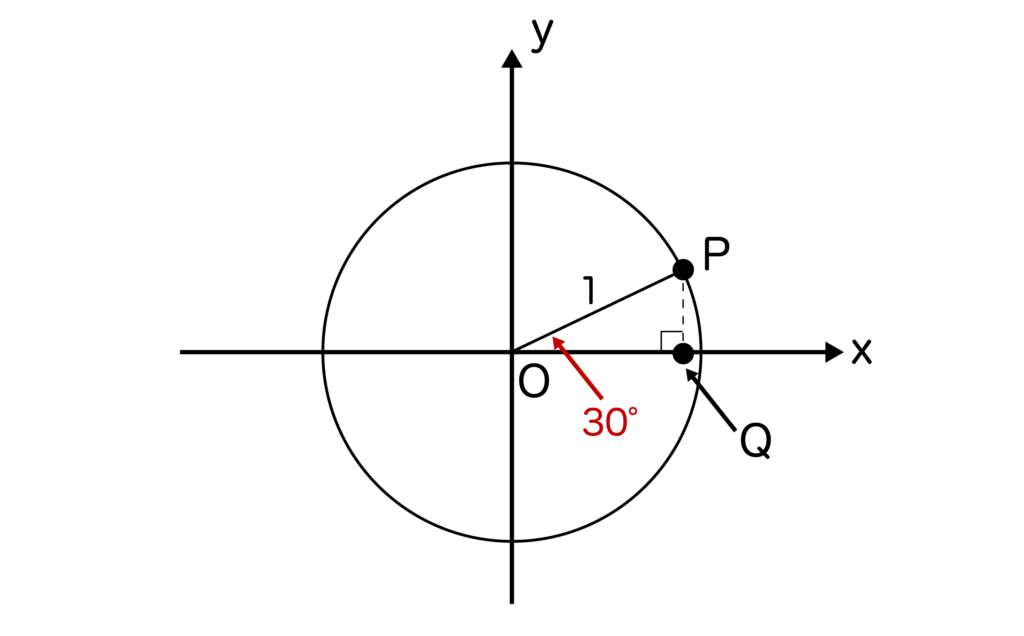
※ちなみにですが、単位円上の点Pの座標を(x、y)とするとsinθ=点Pのy座標=y、cosθ=点Pのx座標=xとなるのでした(sinθ=PQ/PO=PQ=y、cosθ=OQ/PO=OQ=xより)単位円においてsinθ=y、cos=xは公式の1つとして覚えておきましょう。
三角形OPQに注目すると、∠POQ=30度なので三角形OPQは辺の比が1:2:√3の直角三角形であることがわかります。
したがって、OQ=1×√3/2=√3/2、PQ=1×1/2=1/2となります。
以上より、tan30度=PQ/OQ=1/2 ÷ √3/2=1/√3が求まります。
単位円を使ったtan30度の求め方も必ずできるようにしておきましょう。
tan30度の値を三角比の表で確認してみよう
以上でtan30度の値は分数で1/√3と求めることができました。
念のため、以下の三角比の表でもtan30度の値を確認してみましょう。以下の赤枠の部分になりますね。
※三角比の表の見方がわからない人は三角比の表の見方について解説した記事をご覧ください。
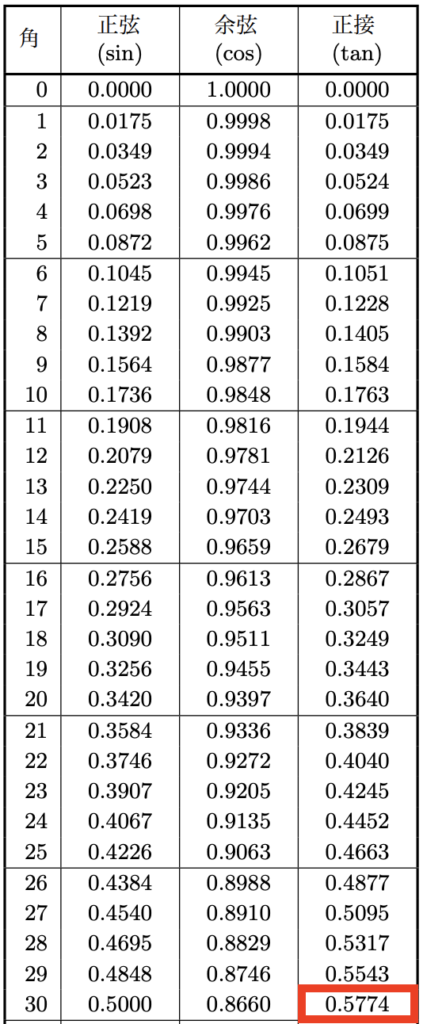
tan30度=0.5774となっています。
tan30度は分数で1/√3でした。√3=1.7320508…([人並みに奢れや]と覚えましょう)より、1÷√3=0.57735…なので、表の通り確かに0.5774となっていることが確認できました。
※「人並みに奢れや」など他にも色々ルートの数の覚え方はあります。詳しくは平方根とは何かについて解説した記事をご覧ください。
tan30度の値はy=1/√3xの傾きとなる
最後にtan30度に関して重要なことを解説しておきます。
tan30度=1/√3ですが、これは一次関数y=1/√3xの傾きと等しくなります。
※一次関数y=axにおいてaのことを「傾き」と呼ぶのでした。詳しくは一次関数の変化の割合・傾きの求め方について解説した記事をご覧ください。
y=1/√3xはxの値が1増加するとyの値が1/√3増加します。先ほど、以下の図を活用してtan30度の値を求めましたね。

tan30度=BC/ACでした。ABを一次関数の直線に見立てると、BC/ACはACの値が1増加したときのBCの増加量を表していることがわかります。
一般的に、tanθと一次関数y=mxにおいてはtanθ=mが成り立ちます。公式の1つとして覚えておきましょう。
※詳しくは2直線のなす角の求め方について解説した記事をご覧ください。
いかがでしたか?今回はtan30度の値の求め方について解説していきました。
自分で図形を書いて求める方法・単位円を使って求める方法どちらもできるようにしておきましょう。