六角形の内角の和は結論から申し上げると720°です。では、なぜ内角の和が720°になるのかを皆様は説明できますでしょうか?
これが説明できないと本当の意味で内角の和を理解しているとは言えないので、必ず説明できるようにしておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者が六角形の内角の和が720°になるのはなぜかについて、図解でわかりやすく解説していきます。
数学や図形が苦手な人でも理解できるように解説していくので、ぜひ最後までお読みください。
六角形の内角の和の求め方その1
六角形の内角の和の求め方1つ目は、実際に六角形を書いてみることです。
今回は以下のように六角形ABCDEFを書いてみます。
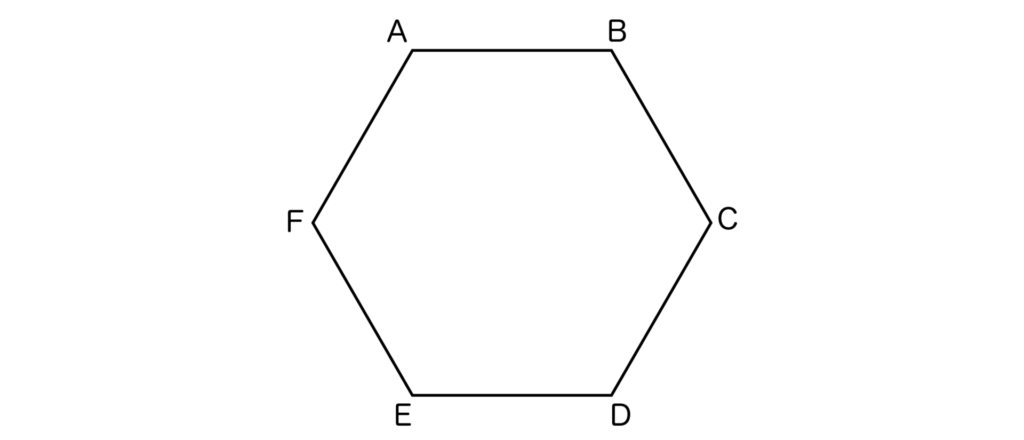
そして、AとC、AとD、AとEを直線で結びます。
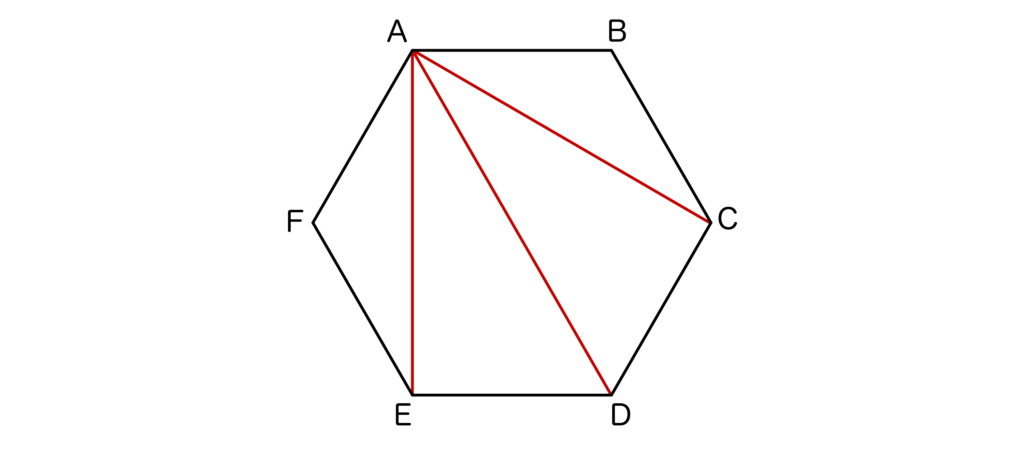
すると、4つの三角形ABC、ACD、ADE、AEFができました。
ここで、三角形の内角の和は180°でした。
六角形は上記のように4つの三角形に分割できるので、六角形の内角の和は4×180°=720°となります。
以上が最もシンプルな六角形の内角の和の求め方です。この求め方は六角形だけでなくどんな多角形にも応用できるので、必ず覚えておきましょう。
六角形の内角の和の求め方その2
内角・外角とは何かについて解説した記事をご覧いただくとわかりますが、n角形の内角の和は(n-2)×180°で求めることができるのでした。
実際にn=3(三角形)を上記の公式にあてはめてみると、(3-2)×180°=180°になります。
三角形の内角の和は180°なので、正しいですね。
n=4(四角形)をあてはめてみると、(4-2)×180°=360°になります。
四角形の内角の和は360°なので、こちらもしっかりと正しいことが確認できます。
六角形の内角の和を求めるには、上記の公式にn=6を代入して、(6-2)×180°=720°になります。
先ほど、六角形を4つの三角形に分割して内角の和を求めましたが、そのときの値と確かに同じ720°になっていることが確認できます。
ちなみにですが、(6-2)×180°=720°において、6-2=4ですが、この4は六角形が4つの三角形に分割できることを意味しています。n角形は(n-2)個の三角形に分割可能です。
以上でご紹介した多角形の内角の和を求める公式は非常に便利なので、必ず覚えておきましょう。
正六角形の1つの内角と外角の大きさ
最後に、正六角形の1つの内角と外角の大きさを求めて本記事を終了とします。
先ほどの通り、六角形の内角の和=720°でした。もちろん正六角形においても内角の和は720°です。
正多角形は1つの内角の大きさは等しいので、正六角形の6つの内角の大きさは全て等しくなります。
よって、正六角形の1つの内角の大きさ=720°÷6=120°となります。
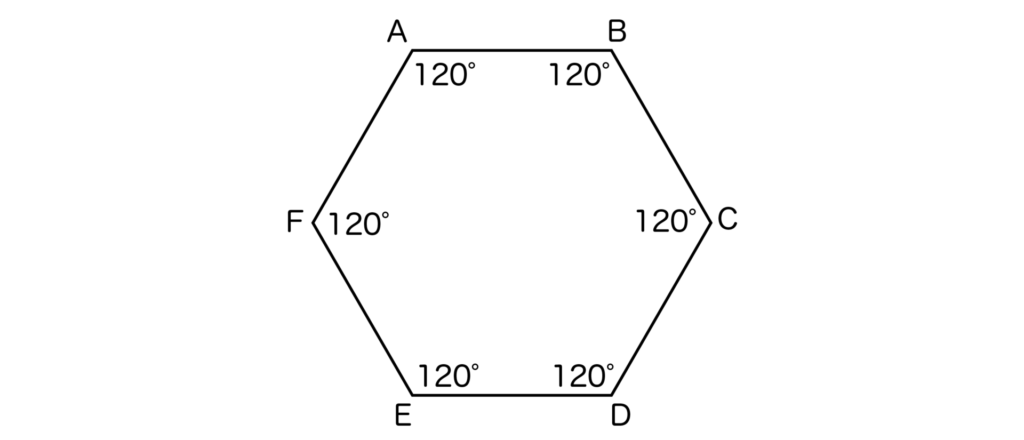
そして、外角=180°-内角なので、正六角形の1つの外角の大きさ=180°-120°=60°となります。
今回は六角形の内角の和が720°なのはなぜかについて解説していきました。
繰り返しにはなりますが、多角形の内角の和を求める公式(n-2)×180°は非常に重要なので、必ず覚えておきましょう。
また、六角形だけでなく、正五角形の内角の大きさを5秒で求める方法について解説した記事もご用意しているので、ぜひ合わせてご覧ください。


