三角形の辺と角の大小とは？わかりやすく解説＆証明・練習問題付き

今回は高校数学の数学1の三角関数の学習で登場する三角形の辺と角の大小を取り上げます。

三角形の辺と角の大小は地味な公式ではありますが、三角形の性質を理解する上では欠かせない公式です。

本記事では早稲田大学教育学部数学科を卒業した筆者が三角形の辺と角の大小とは何かについてわかりやすく解説していきます。

また、三角形の辺と角の大小の証明や練習問題も用意しているので、ぜひ最後までお読みください。

三角形の辺と角の大小とは？公式をご紹介

では早速、三角形の辺と角の大小とは何かについて以下の三角形ABCで解説していきます。

※頂点A、B、Cに向かい合う辺（対辺といいます）BC、CA、ABの長さをそれぞれa、b、cとします。

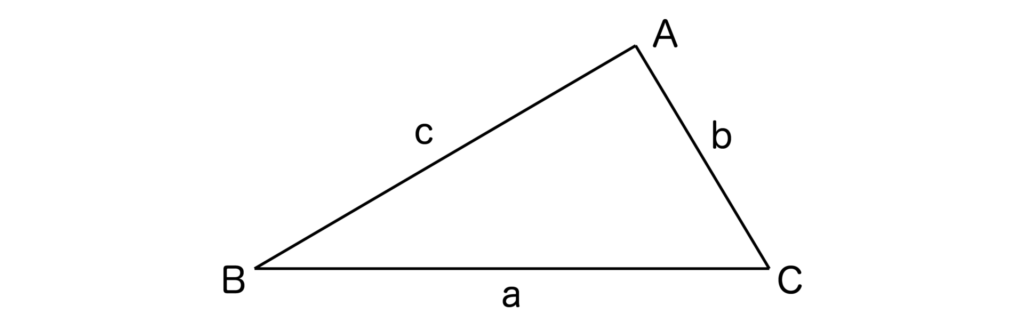
このとき、以下2つが成り立ちます。

[1]

• a<b ⇔ A<B
• a=b ⇔ A=B
• a>b ⇔ A>B

[2]

• A<90° ⇔ a²<b²+c²
• A=90° ⇔ a²=b²+c²（三平方の定理）
• A>90° ⇔ a²>b²+c²

※記号「⇔」の意味がわからない人は命題と条件のコツについて解説した記事をご覧ください。

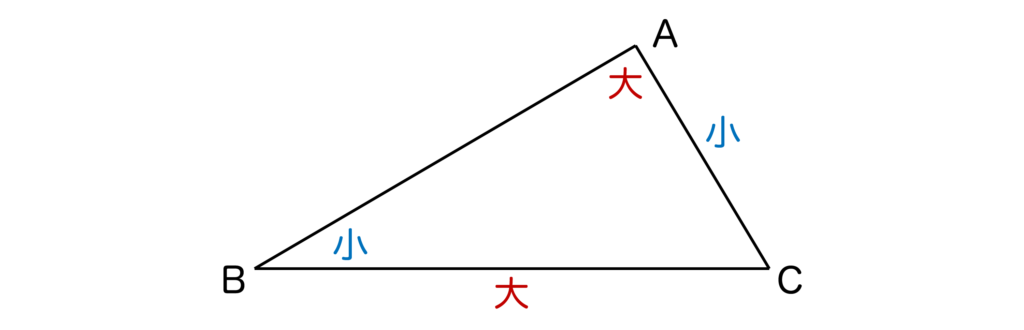
以上が三角形の辺と角の大小の解説となります。直感的にもわかりやすい公式かと思いますので、必ず覚えておきましょう。

三角形の辺と角の大小の証明

では、三角形の辺と角の大小はなぜ成り立つのでしょうか？

ここからは三角形の辺と角の大小の証明を行なっていきます。

【証明】

まずは上記の[1]から証明を行います。

以下の三角形ABCにおいて、a<b ⇔ A<Bを証明します（他も同様にして証明可能です）

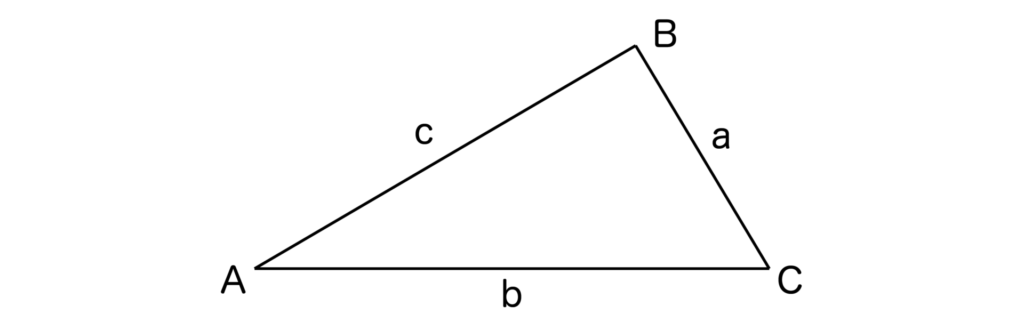
余弦定理より、

cosA-cosB

=（b²+c²-a²）/2bc – （c²+a²-b²）/2ca

= （ab²+ac²-a³-bc²-a²b+b³）2abc・・・①

となりますね。

※余弦定理がわからない人は余弦定理とは何かについて解説した記事をご覧ください。

①の分子

=（a-b）c²+ab²-a³-a²b+b³

= （a-b）c²+（b³-a³）+ab（b-a）

= -（b-a）c²+（b-a）（b²+ab+a²）+ab（b-a）

= （b-a）（-c²+b²+ab+a²+ab）

= （b-a）{（a+b）²-c²}

= （b-a）（a+b+c）（a+b-c）

ここで、三角形の成立条件よりa+b+c>0、a+b-c>0です。

また、2abc>0ですね。

※三角形の成立条件がわからない人は三角形の成立条件とは何かについて解説した記事をご覧ください。

したがって、b-a>0 ⇔ a<b ⇔ cosA-cosB>0 ⇔ cosA>cosB ⇔ 0°<A<B<180°となります。

※0°≦α≦180°、0°≦β≦180°のとき、α<β ⇔ cosα>cosβとなります。

続いては[2]の証明を行います。

∠Aを最大の角とします。

すると、余弦定理より

cosA=（b²+c²-a²）/2bcなので、以下が成り立ちます。

• （鋭角三角形）A<90° ⇔ cosA>0 ⇔ b²+c²-a²>0 ⇔ a²<b²+c²
• （直角三角形）A=90° ⇔ cosA=0 ⇔ b²+c²-a²=0 ⇔ a²=b²+c²
• （鈍角三角形）A>90° ⇔ cosA<0 ⇔ b²+c²-a²<0 ⇔ a²>b²+c²

※A=90°のとき、cosA=0になる理由がわからない人はsin90度が1なのはなぜかについて解説した記事をご覧ください。

三角形の辺と角の大小の練習問題

最後に三角形の辺と角の大小の練習問題を解いてみましょう。

【練習問題】

三角形ABCにおいて、sinA：sinB：sinC=√7：√3：1が成り立つとき、以下の問いに答えよ。

（1）三角形ABCの内角のうち、もっとも大きい角の大きさを求めよ。

（2）三角形ABCの内角のうち、2番目に大きい角の正接を求めよ。

【解答＆解説】

（1）正弦定理より、a/sinA＝b/sinB=c/sinCが成り立ちますね。

※正弦定理がわからない人は正弦定理とは何かについて解説した記事をご覧ください。

よって、a：b：c=sinA：sinB：sinC＝√7：√3：1となります。

したがって最も大きい辺はaとなるので、最も大きい角はAとなります。

ここで、a、b、cはある正の数kを用いてa=√7k、b=√3k、c=kと表すことができるので、余弦定理より

cosA＝（√3k）²+k²-（√7k）² / 2・√3k・k＝-√3/2となります。

よって、A=150°・・・（答）が求まります。

（2）（1）より、2番目に大きい角はBであることがわかります。

余弦定理より、

cosB＝k²+（√7k）²-（√3k）² / 2・k・√7k＝5/2√7となります。

ここで、正接とはtanのことでしたね。

※詳しくは三角比の覚え方について解説した記事をご覧ください。

1+tan²θ＝1/cos²θを使いましょう。

※1+tan²θ＝1/cos²θがわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。

1+tan²B＝1/cos²Bより、

tan²B＝1/cos²B-1＝（2√7/5）²-1＝3/25

A>90°より、B<90°なのでtanB>0となります。

したがって、tanB=√3/5・・・（答）となります。

いかがでしたでしょうか？

今回は三角形の辺と角の大小とは何かについて解説した後、三角形の辺と角の大小の証明を行いました。

今回の記事のように、三角形の辺と角の大小は余弦定理や正弦定理と絡めて使うことが多いので、必ず覚えておきましょう。