sin0度・cos0度の値の求め方は理解していますでしょうか?
結論だけ述べるとsin0度=0、cos0度=1となるのですがそうなる理由を説明できないとこれから先の三角関数の学習でつまずいてしまうのでご注意ください。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin0度とcos0度の値の求め方について数学が苦手な人でも理解できるようにわかりやすく解説していきます。
sin0度とcos0度の値は暗記ではなく「なぜそうなるのか?」の理論をしっかりと理解してください。
sin0度・cos0度の値は?
sin30度の求め方について解説した記事をご覧いただくとわかりますが、三角比(sin・cos・tan)の値を求める方法としては「自分で直角三角形を書く」または「単位円を活用する」の2通りがあります。
しかし、今回のようにsin0度やcos0度など直角三角形を書くことができない場合は単位円を活用してその値を求めることになります。
※単位円=単位円とはxy平面上において原点Oを中心とした半径=1の円のこと。
単位円において点P(x、y)を単位円上に取ると、sinθ=y、cosθ=xになるのでした(sinθ=y/1=y、cosθ=x/1=xより)
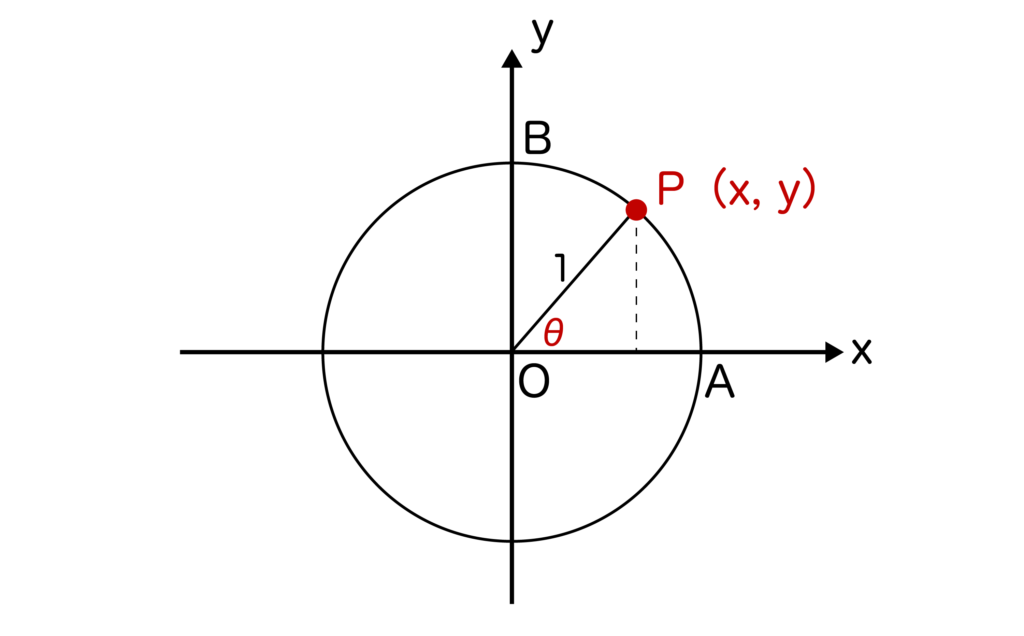
そして、単位円においてもう1つ重要なことは上記の図においてAOをθ=0度とし、θ>0の場合は反時計回りに、θ<0の場合は時計回りに角度を取るのでした。
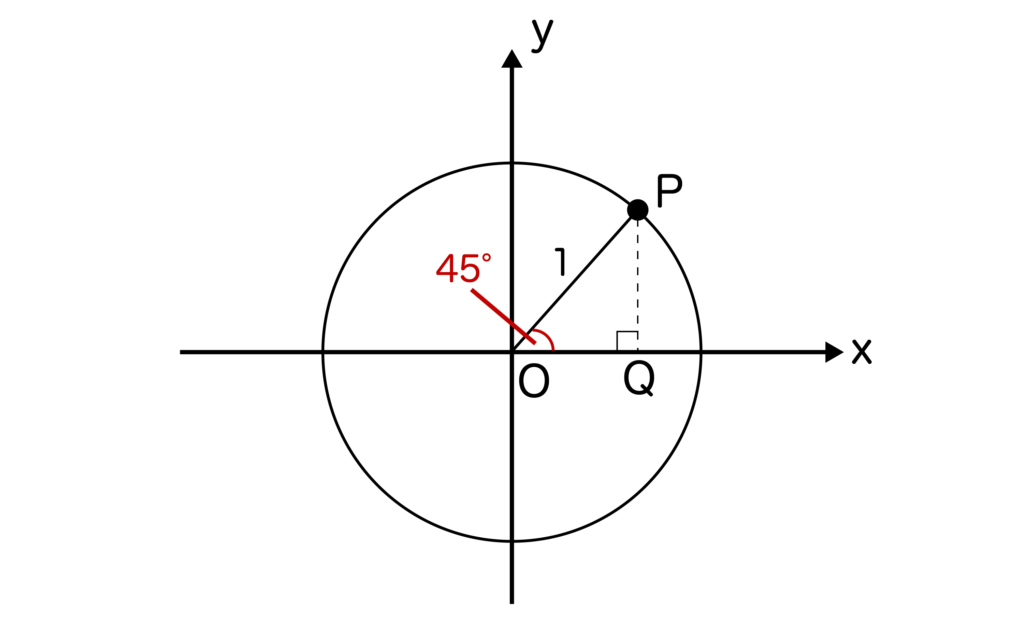
例えば、θ=45度のとき、θ>0なので以下の図のようになります。
※sin45度の求め方について解説した記事もぜひ合わせてご覧ください。
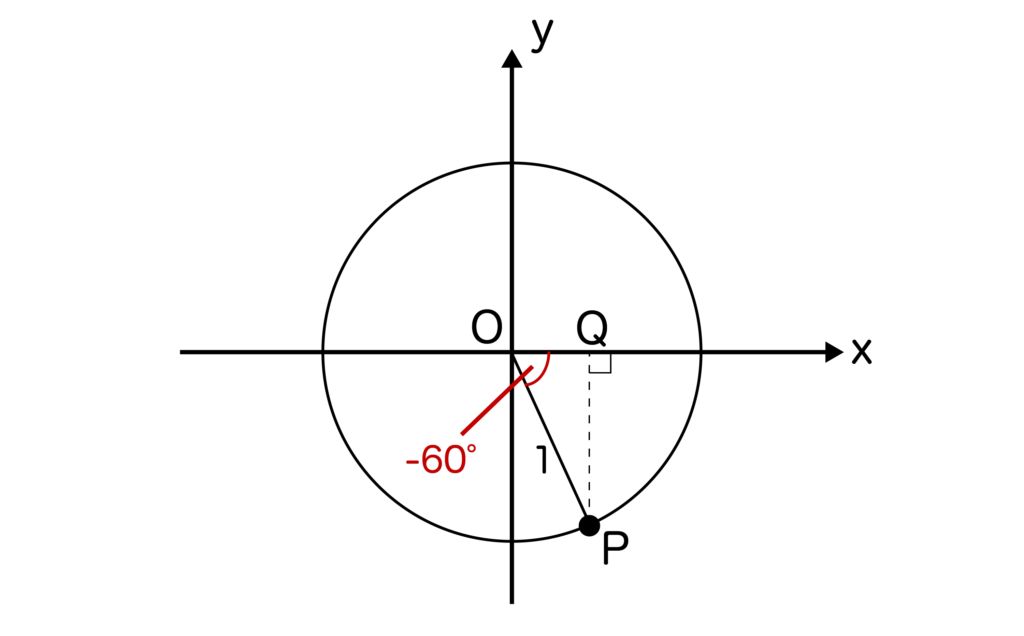
また、例えばθ=-60度のときはθ<0なので以下の図のようになります。
※sin-60度の値の求め方について解説した記事もぜひ合わせてご覧ください。
今回のようにsin0度やcos0度の値を求める場合、θ=0度なので単位円とx軸の交点が点Pとなります。
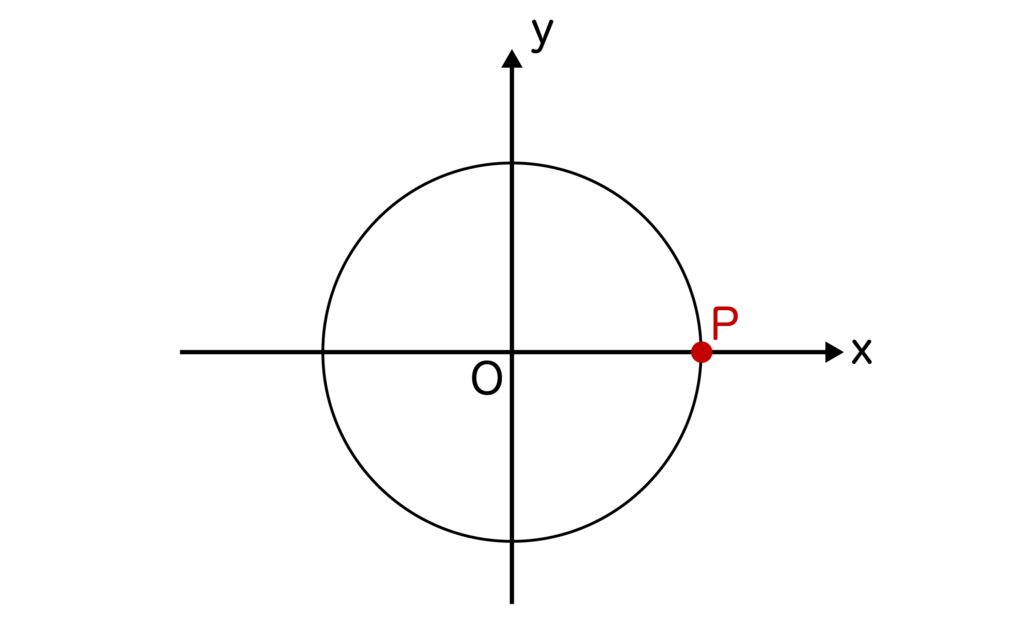
点Pの座標は(1、0)であることからsin0度=y=0、cos0度=x=1となります。
※先ほども解説した通り、単位円においてはsinθ=y、cosθ=xとなるのでした。
以上が単位円を使ったsin0度、cos0度の求め方となります。単位円は大学入試・共通テストでも非常に重要となります。必ず扱えるようにしておきましょう。
sin0度・cos0度の値を三角比の表で確認してみよう
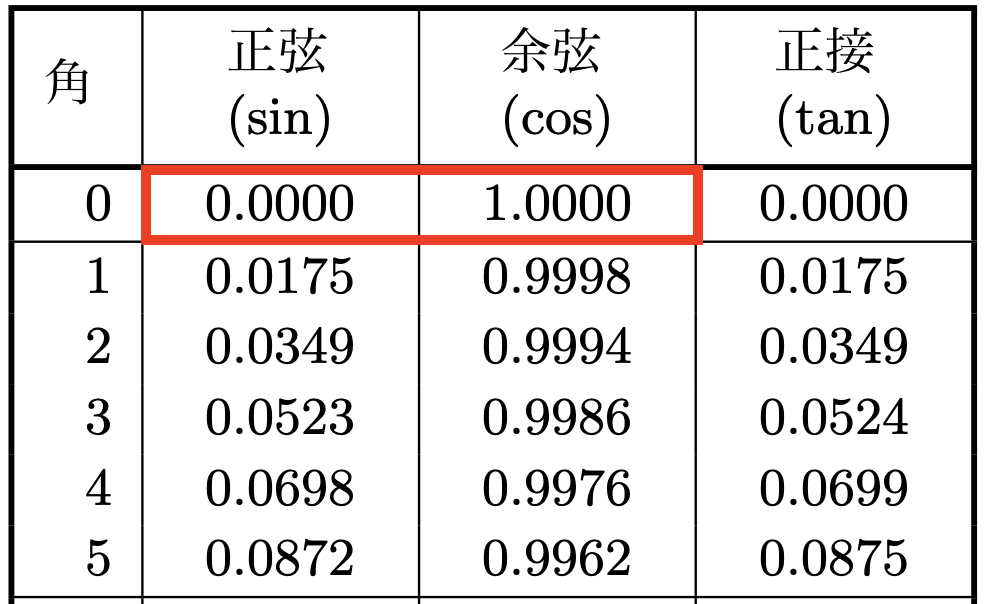
念のため、sin0度=0、cos0度=1となっているかを三角比の表で確認しておきましょう。
以下は三角比の表ですが、確かにsin0度=0、cos0度=1になっていることが確認できます(表の赤枠部分参照)
※表の見方がわからない人は三角比の表の見方について解説した記事をご覧ください。
sin0度・cos0度のとき、tan0度の値は?
では、sin0度=0、cos0度=1のときtan0度の値はどうなるか求めてみましょう。
tan0度の求め方ですが、tanθ=sinθ/cosθの公式を使います。
※tanθ=sinθ/cosθの公式がわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
つまり、tan0度=sin0度/cos0度=0/1=0となることがわかります。tan0度は上記の三角比の表でも確かに0になっていることが確認できますね。
※0/1のように分数の分子=0となる場合、その分数の値は0となります。しかし、分母=0の場合は計算不可となるのでご注意ください。数を0で割ることはできません。
※tan0度について詳しく解説した記事もぜひ合わせてご覧ください。
いかがでしたか?本記事でご紹介した三角比の値をまとめると、
- sin0度=0
- cos0度=1
- tan0度=0
となります。もちろん暗記しても良いですが、なぜその値になるのか?をしっかりと説明できるようにしておきましょう。