sin120度の値は皆様すぐに答えられますでしょうか?
sin120度の値を求めるには単位円を使うのが便利です。単位円は大学入試や共通テストでもよく使うので、これを機に使い方を理解しておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者がsin120度の求め方について図解でわかりやすく解説していきます。
sin120度を分数にすると?求め方は?
では早速、sin120度を求めていきましょう。
sinθの値を求める際に、例えばsin45度などθ<90度である場合は自分で45度型の直角三角形を書くなどしてsinの値を求めることができるのですが、sin120度のようにθ>90度の場合は直角三角形が書けないのでそうはいきません。
※sin45度の求め方について解説した記事もぜひ合わせてご覧ください。
そのような場合は冒頭でも解説した通り単位円を使います。単位円を使えばθがどんな値であっても三角比(sin・cos・tan)を求めることができます。単位円は非常に優秀なツールなのです。
※三角比の求め方について解説した記事もご用意しているので、ぜひ合わせてご覧ください。
単位円とはxy平面上において、原点Oを中心とした半径=1の円のことでした。
そして、以下の図のように単位円上に点P(x、y)を取ると、sinθ=y、cosθ=xとなるのでした。
※詳しくはsin90度が1なのはなぜかについて解説した記事をご覧ください。
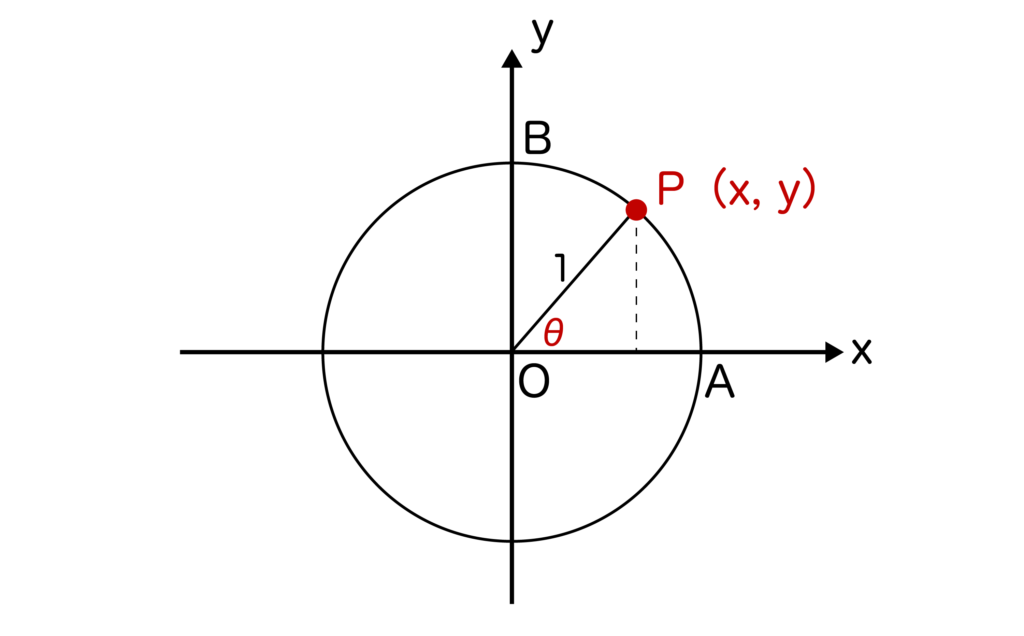
θに関してですが、上記の図においてAOをθ=0度とします。そして、θ>0の場合は反時計回りに、θ<0の場合は時計回りに角度を取ります。
今回はsin120度を求めるのでθ=120度です。θ=120を単位円に取ると、以下のようになります。
※点Pからx軸に対して下ろした垂線とx軸との交点をQとします。
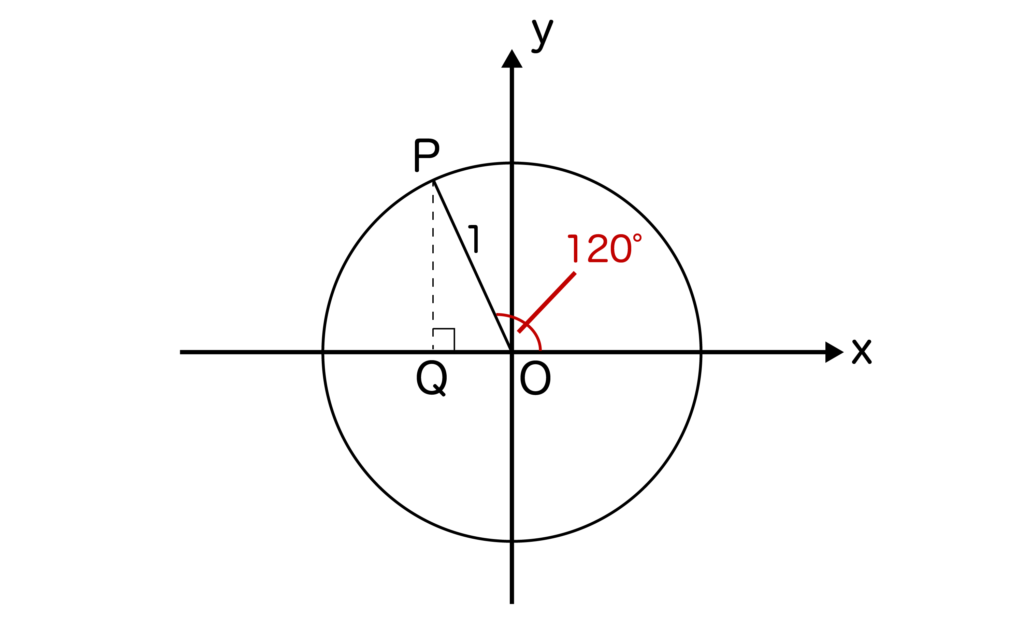
∠POQ=180度-120度=60度となるので、三角形OPQは60度型の直角三角形であることがわかります。
つまり、OP:PQ=2:√3であることがわかります。
ここで、単位円であることからOP=1なので、1:PQ=2:√3より、PQ=√3/2が求まります。
PQ=√3/2ということは、点Pのy座標が√3/2ということですね。
先ほども解説した通り、単位円上に点P(x、y)を取るとsinθ=y、cosθ=xになるので、sin120度=点Pのy座標=√3/2となります。
以上が単位円を使ったsin120度の求め方となります。
手順としては、
- 単位円上にθ(今回は120度)を取る
- 点Pのy座標を求める(それがsinθの値となる)
となります。「sinθ=y、cosθ=x」は非常に重要なので、公式の1つとして必ず覚えておきましょう。
2倍角の公式を使ったsin120度の求め方
三角関数の学習を進めていくと、2倍角の公式というものが登場します。
2倍角の公式とは、sin2α=2sinαcosαが成り立つことです。
※まだ学習していない人は飛ばしていただいて問題ありません。
2倍角の公式を使ってsin120度の値を求めることも可能です。120度=2×60度なので、
sin120度=sin(2×60度)=2・sin60度・cos60度=2・√3/2・1/2=√3/2となります。
※sin60度の求め方について解説した記事もご用意しているので、ぜひ合わせてご覧ください。
2倍角の公式は非常に便利なのでもちろん活用しても良いのですが、単位円を使ったsin120度の求め方も必ずできるようにしておいてください。
sin120度のときcos120度、tan120度の値は?
ついでにcos120度、tan120度も求めておきましょう。
まずはcos120度から求めます。先ほどと同様に単位円上にθ=120度を取りましょう。

OP:OQ=2:1であり、OP=1なので、1:OQ=2:1より、OQ=1/2となりますね。
つまり、点Qのx座標=-1/2=点Pのx座標であることがわかります。マイナスが付くことにご注意ください。
cosθ=点Pのx座標なので、cos120度=-1/2となります。
では、tan120度はどうでしょうか?三角比の関係式・相互関係の公式より、tanθ=sinθ/cosθでしたね。
※詳しくは三角比の関係式・相互関係について解説した記事をご覧ください。
つまり、tan120度=sin120度/cos120度です。
sin120度=√3/2、cos120度=-1/2なので、tan120度=√3/2 ÷ (-1/2)=-√3となります。
いかがでしたでしょうか?
今回はsin120度の求め方について解説していきました。120度は分数で√3/2ですが、暗記するのではなくいつでも自力で求められるようにしておきましょう。