sin150度の値は暗記するのではなく、自力でいつでも求められるようにしておかなければなりません。
自力で三角比(sin・cos・tan)を求めることができなければ、この先の三角関数の学習で必ず苦戦してしまうので、今のうちに求められるようにしておきましょう。
※三角比の覚え方について解説した記事もありますので、ぜひ参考にしてください。
そこで今回は早稲田大学教育学部数学科を卒業した筆者がsin150度の求め方について数学が苦手な人でも理解できるようにわかりやすく解説していきます。
また、sin150度の値がsin30度の値と同じになる理由についても解説していきます。
sin150度の求め方
sinθやcosθ、tanθの値を求めるとき、θ>90度の場合は単位円を使ってその値を求めるのが定石です。
そして、重要なことは単位円の円周上に点P(x、y)を取ると、sinθ=y、cosθ=xが成り立つことです。
※sinθ=y、cosθ=xが成り立つ理由についてはsin90度が1なのはなぜかについて解説した記事をご覧ください。
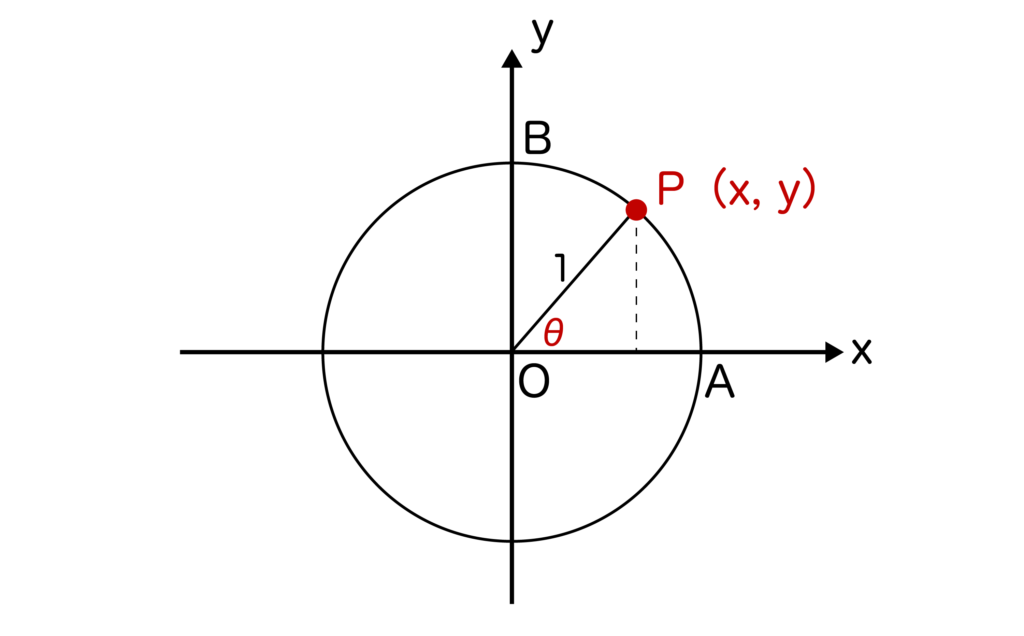
単位円におけるsinθ=y、cosθ=xは三角関数の公式の1つとして必ず覚えておきましょう。
以上を理解した上で、単位円においてθ=150度を取ると以下のようになりますね(点Pからx軸に対して下ろした垂線とx軸との交点を点Qとする)
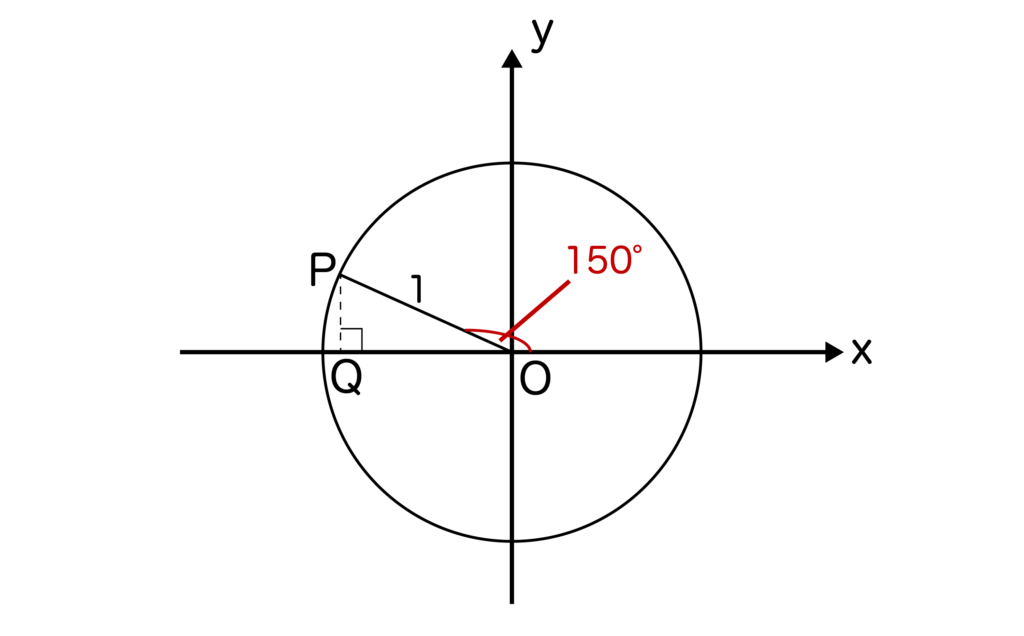
すると、∠POQ=180度-150度=30度となるので、三角形OPQは辺の比が1:2:√3の直角三角形となることがわかります。
単位円なので、OP=1に注目すると、PQ=1×1/2=1/2となりますね。
つまり、Pのy座標が1/2となります。
したがって、sin150度=点Pのy座標=1/2となります。
以上が単位円を利用したsin150度の求め方となります。単位円は三角関数の分野においては非常に重要で、大学入試や共通テストでも利用機会は多いです。必ず使えるようにしておきましょう。
sin150度がsin30度と同じになる理由
以上えsin150度=1/2を求めることができましたが、これはsin30度と同じ値になっています。
※sin30度が分数で1/2になる理由について解説した記事もぜひ合わせてご覧ください。
つまり、sinθ=1/2を解くとθ=30度、150度になるということです(0°<θ<360°の場合)
というわけで、ここからはsinθ=1/2が30度、150度になる理由を解説していきます。
今回もまた単位円を使います。先ほども解説した通り、単位円上に点P(x、y)を取ると、sinθ=y、cosθ=xになるのでした。

なので、sinθ=1/2を解くときは、単位円上にy=1/2を引いてみます(以下の図参照)
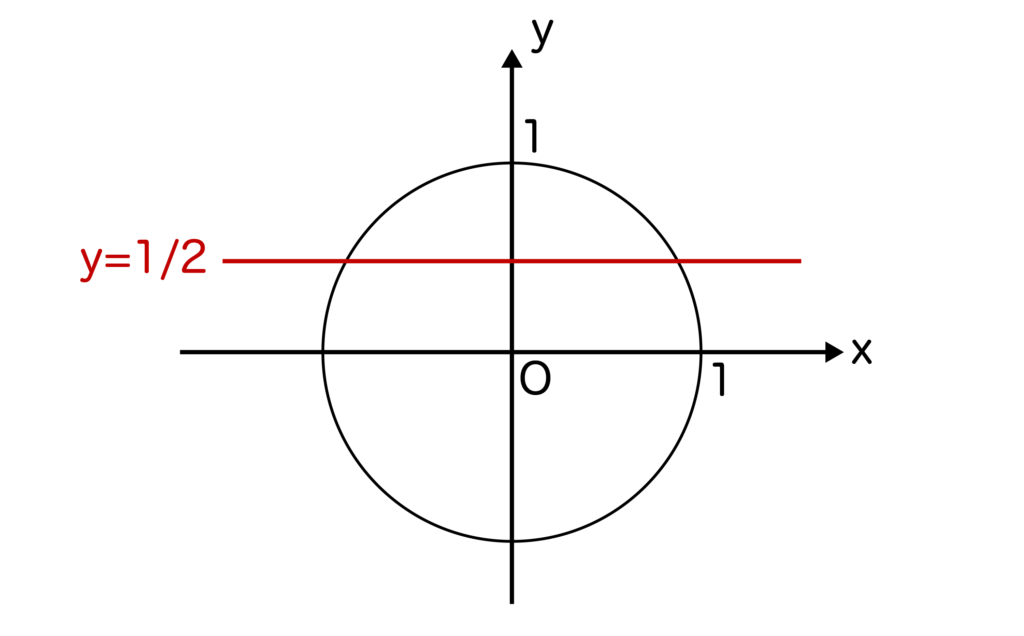
すると、y=1/2と単位円の交点は以下のように2つあることがわかります(点P、点Qとします)
そして、それぞれの交点からx軸に対して垂線を下ろし、x軸との交点をそれぞれ点R、点Sとします。
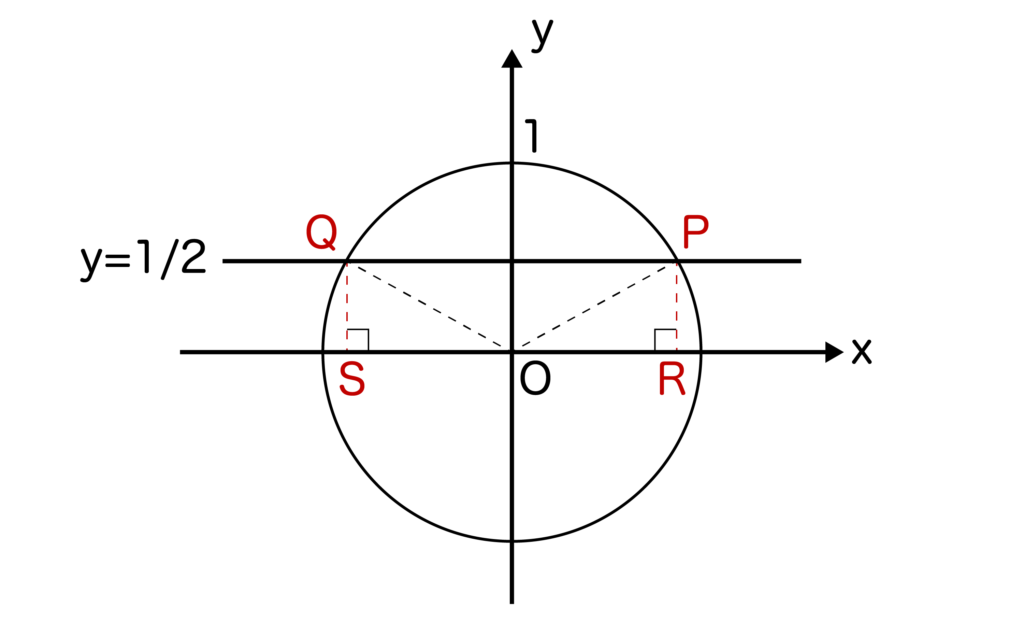
すると、∠ROPと∠ROQが求めるθの大きさということになりますね。
単位円なので、OP=OQ=1です。そして、PR=QS=1/2です。
よって、三角形OPR、OQSはともに辺の比が1:2:√3の直角三角形であることがわかります。
したがって、∠ROP=30度、∠ROQ=150度となるわけです。
以上がsinθ=1/2からθを求める方法です。確かにsin30度、sin150度は同じ値になることがわかりましたね。
このように、単位円はθの値を求めることもできる非常に優秀なツールです。繰り返しにはなりますが、必ず使えるようにしておきましょう。
sin150度を加法定理で求めてみよう
先ほどは単位円を使ってsin150度を求めましたが、加法定理を使ってsin150度を求めることも可能です。
加法定理とは以下の公式のことでした(今回使用する加法定理のみをピックアップします)
sin(α+β)=sinαcosβ+cosαsinβ
※加法定理をまだ学習していない人は飛ばしていただいて問題ありません。
150度=60度+90度なので、
sin150度=sin(60度+90度)=sin60度・cos90度+cos60度・sin90度=√3/2・0+1/2・1=1/2となります。
※sin60度の求め方について解説した記事やsin90度の求め方について解説した記事もご用意しているので、ぜひ参考にしてください。
単位円を使って求めたsin150度の値と確かに一致していることが確認できます。
加法定理も三角関数の分野においては非常に重要です。両方とも使えるようにしておきましょう。
sin150度のとき、cos150度とtan150度の求め方は?
sin150度の値は求めることができましたが、cos150度とtan150度の値はどうなるでしょうか?
まずはcos150度から求めましょう。今回も単位円を使います。先ほどと同様に単位円においてθ=150度を取りましょう。

三角形OPQは30度型の直角三角形なので、OQ=OP×√3/2=1×√3/2=√3/2となります。
つまり、点Qのx座標=点Pのx座標=-√3/2となりますね(マイナスが付くことに注意)
cosθ=点Pのx座標なので、cos150度=-√3/2となります。
残りのtan150度ですが、tanθ=sinθ/cosθを使います。
※tanθ=sinθ/cosθがわからない人は三角比の関係式・相互関係について解説した記事をご覧ください。
tan150度=sin150度/cos150度=1/2 ÷ (-√3/2)=-1/√3となります。
以上をまとめると、
- sin150度=1/2
- cos150度=-√3/2
- tan150度=-1/√3
となります。ぜひ何度も本記事を読み返して、いつでも自力で三角比を求められるようにしましょう。
いかがでしたか?
今回はsin150度の求め方&sin150度がsin30度と値が同じになる理由について解説しました。
単位円の使い方は使う機会を増やせば増やすほど自然に慣れていきます。ぜひたくさんの三角関数に関する練習問題を積んでいってください。