二等辺三角形の辺の長さの求め方を図解でわかりやすく解説！

「二等辺三角形の辺の長さはどうやって求めてればいいのだろうか？」と疑問に思っている人は多いのではないでしょうか？

二等辺三角形の辺の長さの求め方は全然難しくないので、ご安心ください。

今回は早稲田大学教育学部数学科を卒業した筆者が二等辺三角形の辺の長さの求め方を図解でわかりやすく解説していきます。

数学や図形問題が苦手な生徒でも理解できるように解説しているので、ぜひ参考にしてください。

二等辺三角形の辺の長さの求め方その1

1つ目は二等辺三角形の底辺と高さがわかっている場合です。

以下の図のように、BC（底辺）＝18、AD＝30の二等辺三角形ABCにおいて、AB（AC）の辺の長さを求めてみましょう。

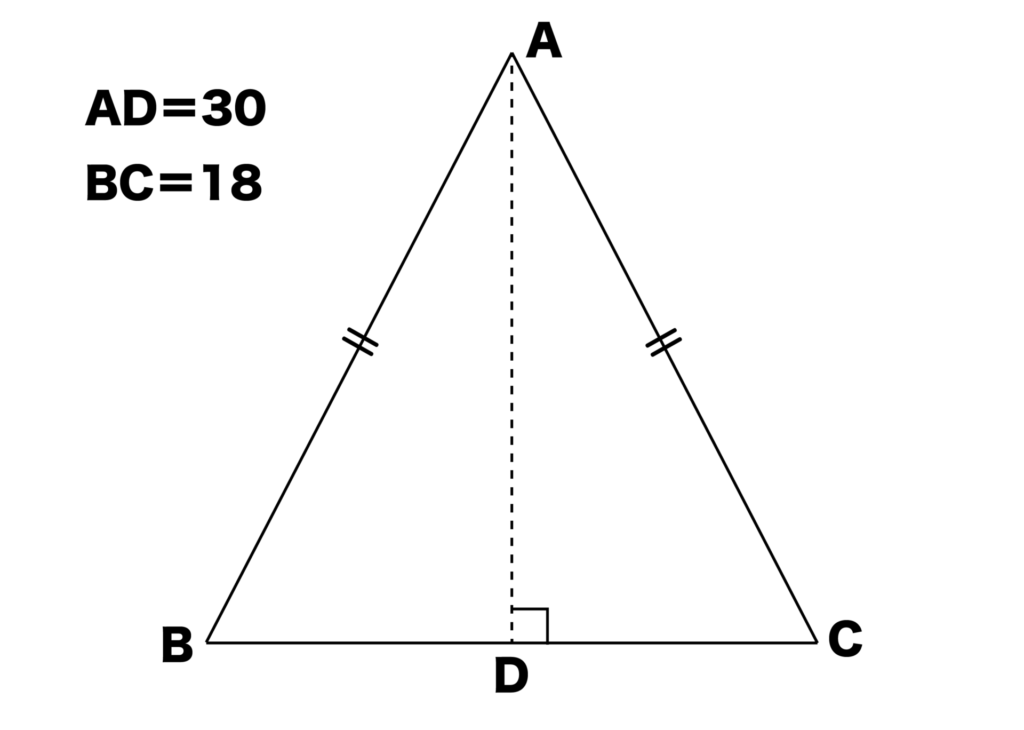
頂角である点Aから底辺であるBCに対して垂線ADをおろしたとき、ADはBCの垂直二等分線になるのでした。

※詳しくは二等辺三角形の定義と定理（性質）について解説した記事をご覧ください。

よって、BD＝BC÷2＝18÷2＝9となります。

ここで、三角形ABDに注目すると三角形ABDは直角三角形なので、三平方の定理が使えます。

AB²＝AD²＋BD²より、AB²＝30²＋9²＝900＋81＝981となります。

ABは辺の長さなので、AB>0です。したがって、AB＝√981＝3√109となります。

※AB2＝981からAB＝3√109になる理由がわからない人は平方根とは何かについて解説した記事をご覧ください。

二等辺三角形では底辺と高さがわかっていれば残りの2の辺の長さも求められます。

※二等辺三角形の底辺の長さの求め方について詳しく解説した記事もぜひ合わせてご覧ください。

二等辺三角形の辺の長さの求め方その2

次は以下の図のように、BC（底辺）＝16、AB＝AC＝20の二等辺三角形ABCにおいて、AD（高さ）の辺の長さを求めてみましょう。

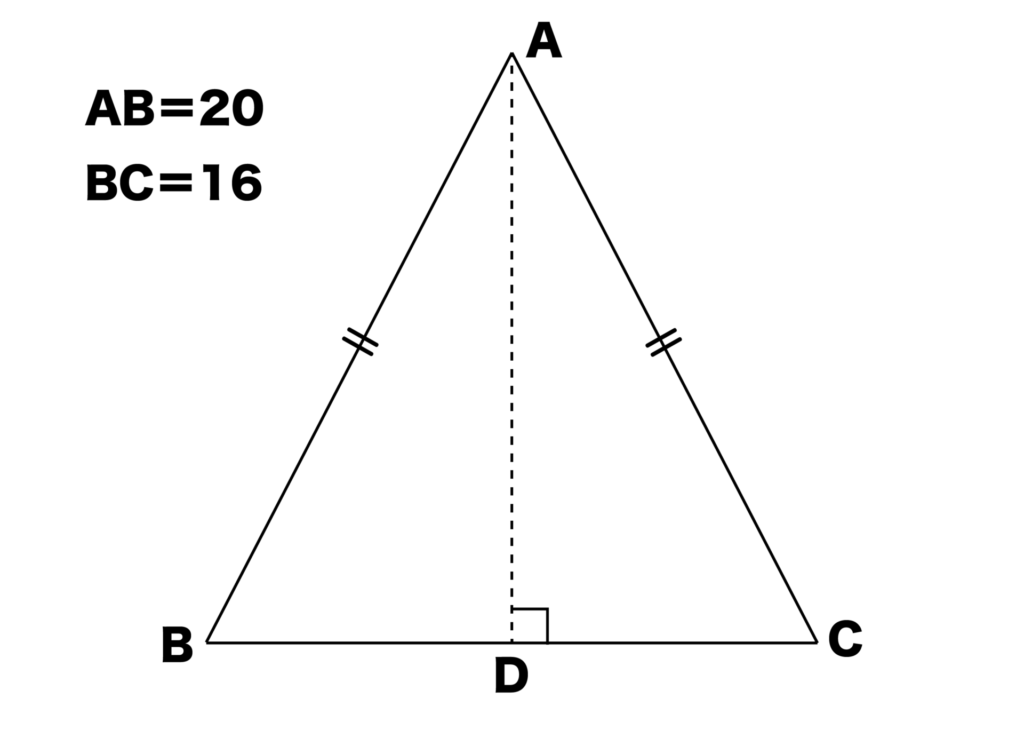
先ほども解説した通り、点DはBCの中点となるので、BD＝8となります。

ここで、三角形ABDに注目すると、三角形ABDは直角三角形なので三平方の定理より、

AB²＝AD²＋BD²

が成り立ちます。

よって、20²＝AD²＋8²より、AD²＝400-64＝336となります。

AD>0より、AD＝√336＝4√21が求まります。

二等辺三角形では底辺と頂角からの2辺の長さがわかっていれば高さも求められます。

※二等辺三角形の高さの求め方について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。

二等辺三角形と三平方の定理は非常に相性が良いので、必ず使いこなせるようにしておきましょう。

二等辺三角形と三平方の定理の関係について解説した記事もご用意しているので、ぜひ合わせてご覧ください。

ちなみにですが、二等辺三角形の高さがわかれば、二等辺三角形の面積も求めることが可能になります。

上記の二等辺三角形の面積＝BC×AD÷2＝16×4√21÷2＝32√21となります。

二等辺三角形の高さを自力で求めてから面積を計算するという手法は非常に重要ですので、必ずできるようにしておきましょう。

二等辺三角形の面積の求め方について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。

二等辺三角形の辺の長さの求め方その3

次は頂角が120°である二等辺三角形の場合です。

次は以下の図のように、∠A＝120°、AB＝AC＝10の二等辺三角形ABCにおいて、AC（底辺）とAD（高さ）の辺の長さを求めてみましょう。

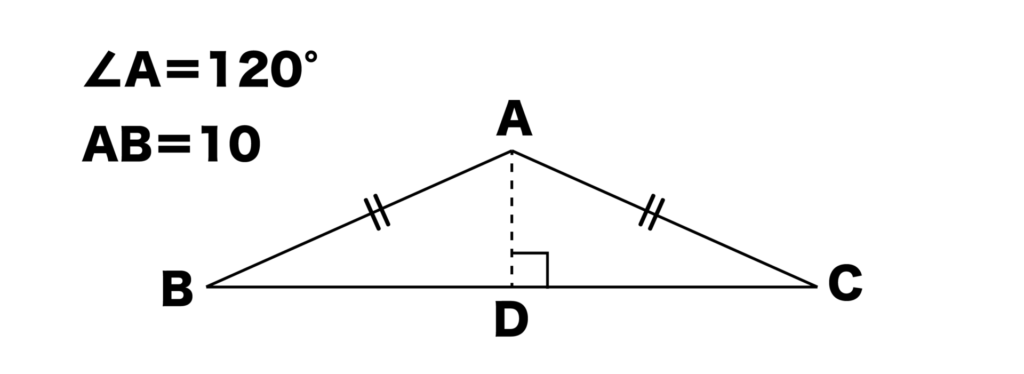
頂角である点AからBCに対しておろした垂線は∠Aの二等分線になるのでした。

よって、∠BAD＝∠CAD＝60°となります。

※二等辺三角形辺の角度の求め方について解説した記事もぜひ合わせてご覧ください。

ここで、三角形ABDに注目すると、∠BAD＝60°、∠BDA＝90°であることから∠ABD＝30°となります。

※三角形の内角の和＝180°でした。詳しくは内角・外角とは何かについて解説した記事をご覧ください。

つまり、三角形ABDは60°型の直角三角形となるので、AD：AB：BD＝1：2：√3となります。

よって、AB＝10より、AD＝10/2＝5となります。

また、BD＝AD・√3＝5√3なので、BC＝BD・2＝10√3となります。

頂角＝120°の二等辺三角形は60°型の直角三角形を上手く生み出すのがポイントとなります。

直角二等辺三角形の辺の長さの求め方も合わせて学習しておこう

以上で二等辺三角形の辺の長さの求め方を解説していきましたが、二等辺三角形の一種である直角二等辺三角形にはまた別の求め方が存在するので、これを機に一緒に学習しておくことをおすすめします。

直角二等辺三角形の辺の長さを10秒で求める方法について解説した記事をご用意しているので、ぜひそちらをご覧ください。

内容は全然難しくないので、数学が苦手な人でも安心してお読みいただけます。

いかがでしたか？

今回は二等辺三角形の辺の長さの求め方について解説していきました。

繰り返しにはなりますが、二等辺三角形と三平方の定理は非常に相性が良いです。

頂角から底辺に対して垂線をおろすというテクニックは非常に重要なので、必ず頭に入れておきましょう。