直角二等辺三角形の辺の長さに関しては、1辺の長さがわかっていれば残りの2辺の長さも必ず決定します。
そして、直角二等辺三角形のすべての辺の長さは10秒もあれば求まります。
というわけで今回は早稲田大学教育学部数学科を卒業した筆者が直角二等辺三角形の辺の長さを10秒で求める方法について図解でわかりやすく解説します。
数学や図形が苦手な人でも理解できる内容になっているので、ぜひ最後までお読みください。
直角二等辺三角形の辺の長さの求め方その1
直角二等辺三角形の辺の長さの求め方は大きく2つあるので、まずは1つ目をご紹介します。
それは、三平方の定理を活用することです。
三平方の定理はピタゴラスの定理とも呼ばれており、以下の直角三角形ABCにおいて、AB2=AC2+BC2が成り立つという公式でした。
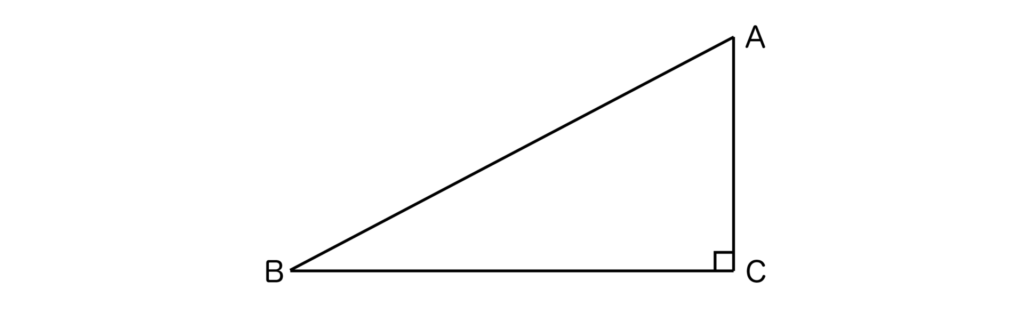
これをもとにして、直角二等辺三角形の辺の長さを求めてみましょう。
斜辺の辺の長さがわかっているとき
まずは斜辺の辺の長さだけがわかっているとき、残りの2辺の長さを三平方の定理を使って求めてみましょう。
以下の直角二等辺三角形ABCにおいて、AB=20であるとき、ACとBCの辺の長さを求めます。
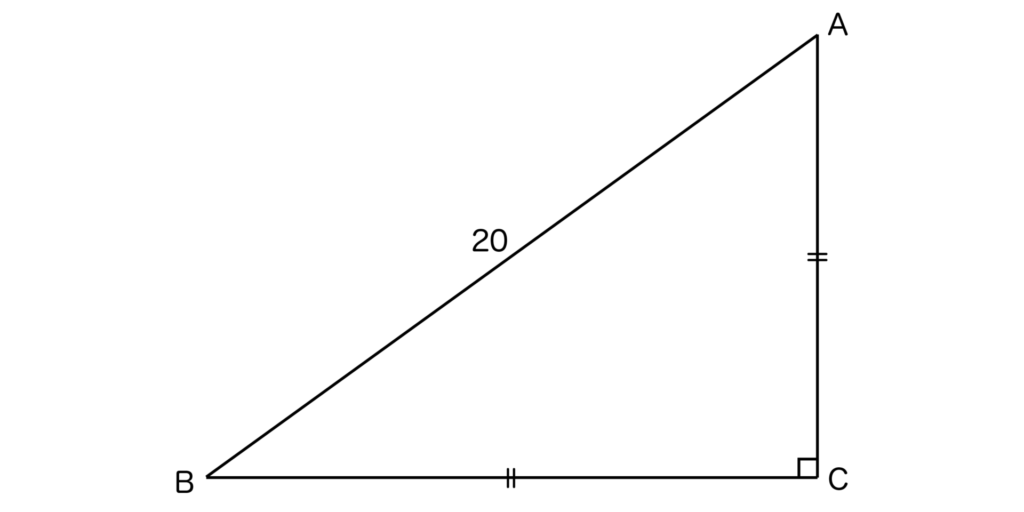
直角二等辺三角形なので、AC=BCとなります。
AC=BC=xとおきましょう。
すると、三平方の定理より202=x2+x2が成り立ちます。
式を整理して、400=2x2より、x2=200となります。
xは辺の長さであることから、x>0なのでx=√200=10√2となります。
※x2=200からx=10√2になる理由がわからない人は平方根とは何かについて解説した記事をご覧ください。
つまり、AC=BC=10√2となります。
斜辺以外の辺の長さがわかっているとき
続いては、斜辺以外の辺の長さがわかっているケースです。
以下の図のように、AC=15の直角二等辺三角形ABCのABとBCの辺の長さを求めましょう。
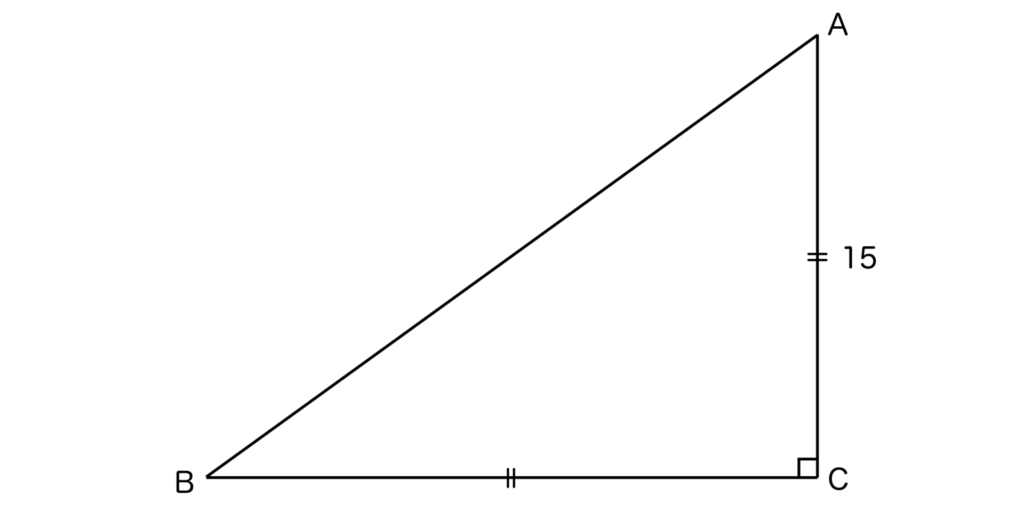
直角二等辺三角形なので、AC=BCです。よって、BC=15となります。
また、三平方の定理より、AB2=AC2+BC2が成り立ちます。AC=BC=15なので、
AB2=152+152=225+225=450となります。
ABは辺の長さなので、AB>0です。よってAB=√450=15√2となります。
以上が三平方の定理を使った直角二等辺三角形の辺の長さの求め方です。
二等辺三角形と三平方の定理の関係について解説した記事もご用意しているので、ぜひ合わせてご覧ください。
直角二等辺三角形の辺の長さを10秒で求める方法
以上で三平方の定理を使った直角二等辺三角形の辺の長さの求め方をご紹介しましたが、毎回三平方の定理を使っていては時間がかかってしまいます。
ここからは三平方の定理を使わずに直角二等辺三角形の辺の長さを10秒で求める方法をご紹介します。
それは、直角二等辺三角形の辺の長さの比を覚えておくことです。
直角二等辺三角形の辺の比は以下の図のように、必ず1:1:√2になります。
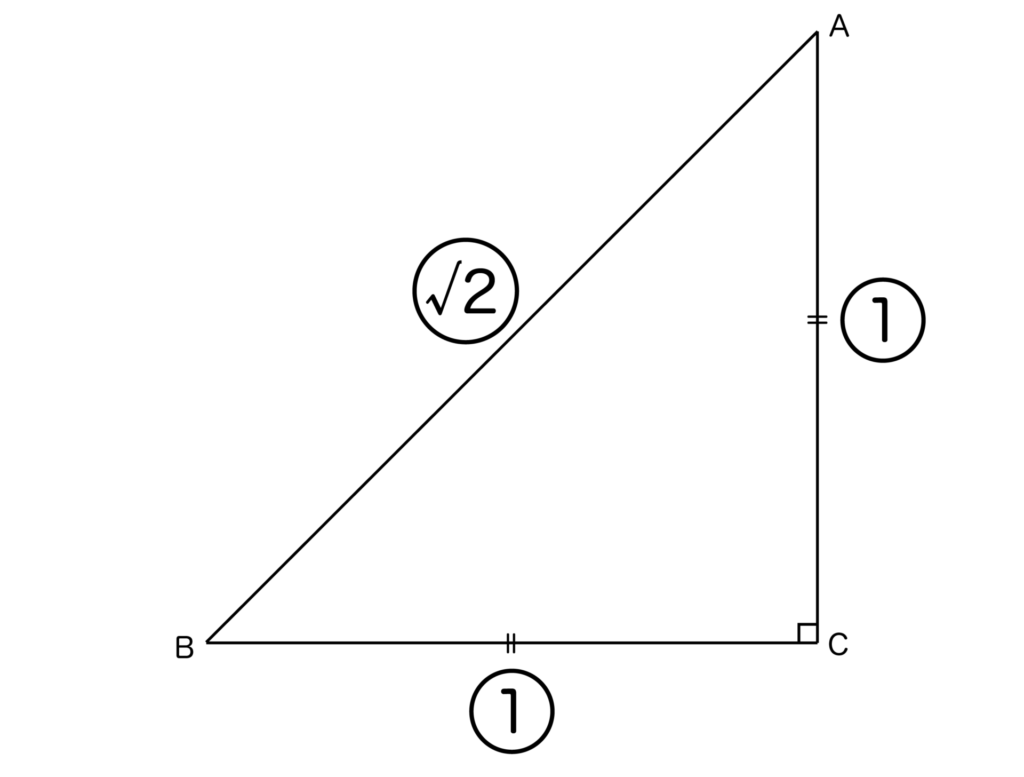
直角二等辺三角形の辺の比が必ず1:1:√2になる理由ですが、上記の図においてAC=BC=aとおくと、三平方の定理より、
AB2=AC2+BC2=a2+a2=2a2が成り立ちます。
AB>0より、AB=a√2となります。
よって、AC:BC:AB=a:a:a√2より、1:1:√2になっていることがわかります。
この直角二等辺三角形の辺の比=1:1:√2を暗記しておけば直角二等辺三角形の辺の長さを10秒で求めることができます。
斜辺の辺の長さがわかっているとき
今度は直角二等辺三角形の辺の比=1:1:√2を使って以下のAB=20の直角二等辺三角形ABCのACとBCの辺の長さを求めてみましょう。

AC=BCで、AC(BC)を求めるにはABの辺の長さを√2で割れば良いので、AC=BC=20÷√2=10√2となります。
三平方の定理を使ってAC、BC辺のの長さを求めたときと確かに同じ値になっていることが確認できます。
斜辺以外の辺の長さがわかっているとき
次は斜辺以外の辺の長さがわかっているときです。
先ほどと同様にAC=15の直角二等辺三角形ABCのABの辺の長さを辺の比を使って求めます。

ABはAC(BC)の辺の長さの√2倍にあたるので、AB=AC×√2=15√2となります。
こちらも三平方の定理を使ってABを求めたときと確かに同じ値になっていることが確認できます。
直角二等辺三角形の辺の比=1:1:√2は超重要なので、必ず覚えておきましょう。
いかがでしたか?
今回は直角二等辺三角形の辺の長さを10秒で求める方法をご紹介しました。
三平方の定理はもちろん重要ですが、直角二等辺三角形の辺の長さを求めるには必ず辺の比を使って時間を効率的に使うことを意識してください。
※二等辺三角形の辺の長さの求め方について解説した記事もご用意しているので、ぜひ合わせてご覧ください。