重複組み合わせHの公式と計算！なぜその公式になるのかも解説

高校数学の数学Aにおける組み合わせの分野では重複組み合わせとが登場します。

重複組み合わせは大学入試や共通テストでも出題されるケースがあるので、必ずできるようしておきましょう。

今回は早稲田大学教育学部数学科を卒業した筆者が重複組み合わせHの公式・計算方法について解説した後、重複組み合わせはなぜその公式になるのか？についても解説していきます。

また、重複組み合わせの問題もいくつか用意しているので、ぜひ最後までご覧ください。

重複組み合わせHの公式と計算

重複組み合わせとは異なるn個のものから重複を許してr個取る組み合わせのことです。

重複組み合わせはHで表現され、重複組み合わせの総数は_nH_r＝_n+r-1C_rとなります（n<rでも問題ありません）

Hは「homogeneous product（同次積）」の頭文字を取ったものです。

重複を許してr個取る「組み合わせ」なので、重複順列と混同しないようにご注意ください。

※重複順列とは何かについて解説した記事もぜひ参考にしてください。

重複順列はr個取り出して並べるので、順序も考慮します。しかし、重複組み合わせは並べる順序は考慮しません。

※順序を考慮するのが順列で、考慮しないのが組み合わせでしたね。詳しくは組み合わせについて解説した記事をご覧ください。

重複組み合わせHの公式はなぜ成り立つ？

重複組み合わせHの公式はなぜ成り立つのか解説する前に、以下の例題を1つ解いてみましょう。

【例題】

桃、柿、リンゴが販売されている。この中から5つを購入するとき、何通りの買い方があるか求めよ。ただし、1つも購入しないものがあっても良いものとする。

【解答＆解説】

買い物かごの中に2個の仕切り（|）を入れ、左側に桃、真ん中に柿、右側にリンゴを入れるとします。

以下は一例となります。

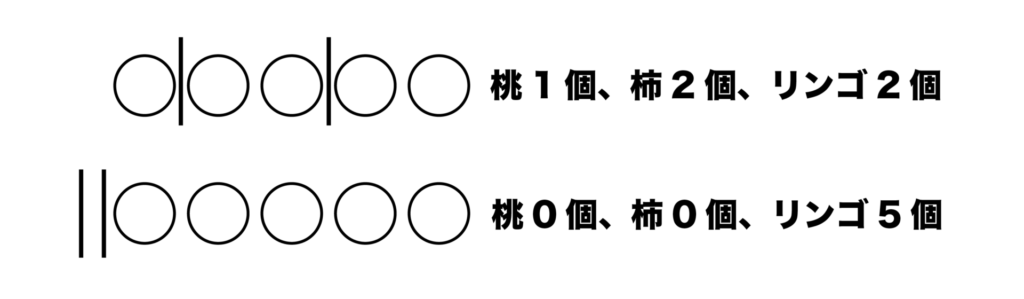
以上のように考えると、5個の◯と2個の|の順列の総数が、3種類の果物から5個を購入する買い方の総数に一致します。

これは同じものを含む順列で3+5-1=7個の場所から5個の◯の場所を選ぶ組み合わせの数に等しくなるので、_3+5-1C₅＝₇C₅＝₇C₂＝21[通り]・・・（答）となります。

一般に、異なるn個のものから重複を許してr個を取る組み合わせの総数は、上記と同じ考え方でr個の◯とn-1個の区切り（|）の順列の総数に一致します。

つまり、（n-1）+r個の場所からr個の◯の場所を選ぶことなので、

_（n-1）+rC_r＝_n+r-1C_r

となるのです。

重複組み合わせの基本問題

重複組み合わせの公式を覚えたところで、まずは重複組み合わせの基本問題を解いてみましょう。

【問題】

（1）1、2、3、4の4個の数字から重複を許して3個の数字を取り出す。このとき、作られる組の総数を求めよ（含まれない数字があってもよいものとする）

（2）p、q、rの3種類の文字から作られる6次の項は全部で何通りあるか求めよ。ただし、含まれない文字があってもよいものとする。

【解答＆解説】

（1）3つの◯で数字、3つの|で仕切りを表し、

• 1つ目の仕切りの左側に◯がある＝数字1
• 1つ目と2つ目の仕切りの間に◯がある＝数字2
• 2つ目と3つ目の仕切りの間に◯がある＝数字3
• 3つ目の仕切りの右側に◯がある＝数字4

とします。

例えば、◯◯||◯|は（1、1、3）を表し、|◯|◯|◯は（2、3、4）を表します。

このとき、求める組の総数＝3つの◯と3つの|の順列の総数なので、₆C₃=20[通り]・・・（答）となります。

（2）6つの◯を使ってx、y、zを表し、2つの|で仕切りを表すとします。

例えば、◯◯◯|◯|◯◯はx³yz²を表します。

すると、求める組の総数は6つの◯と2つの|の順列の総数なので₈C₆＝₈C₂＝28[通り]・・・（答）となります。

重複組み合わせを利用した整数解の個数

【問題】

x+y+z=9を満たす負ではない整数x、y、zの組は全部で何個あるか求めよ。

【解答＆解説】

等式を満たすx、y、zの組は9個の◯と2個の仕切り|の順列を作り、仕切りで分けられた3ヶ所の◯の個数を左から順番にx、y、zとすると得られますね。

よって、求める組の個数は9個の◯と2個の|を一列に並べる順列の総数となるので、₁₁C₂=55[個]・・・（答）となります。

重複組み合わせを利用した数字の順列に関する問題

【問題】

以下の条件を満たす整数の組（a₁、a₂、a₃、a₄、a₅）の個数を求めなさい。

（1）0<a₁<a₂<a₃<a₄<a₅<9

（2）0≦a₁≦a₂≦a₃≦a₄≦a₅≦3

（3）a₁＋a₂＋a₃＋a₄＋a₅≦3、a_i≧0（i=1、2、3、4、5）

【解答＆解説】

（1）1、2、3・・・7、8の8個の数字から異なる5個を選び、それを小さい順にa₁、a₂、a₃、a₄、a₅とすると条件を満たす組が1つに決まるので、₈C₅=₈C₃=56[個]・・・（答）となります。

（2）0、1、2、3の4個の数字から重複を許して5個を選び、それを小さい順にa₁、a₂、a₃、a₄、a₅とすると条件を満たす組が1つ決まるので、₄H₅=_4+5-1C₅=₈C₅=56[個]・・・（答）となります。

（3）3-（a₁＋a₂＋a₃＋a₄＋a₅）＝kとおきます。

すると、a₁＋a₂＋a₃＋a₄＋a₅+k＝3・・・（※）となりますね。

a_i≧0（i=1、2、3、4、5）、k≧0より、求める組の個数は（※）を満たす0以上の整数の組の個数に等しくなりますね。

これは異なる6個から3個取る重複組み合わせの総数なので、₆H₃=_6+3-1C₃=₈C₃=56[個]・・・（答）となります。

今回は重複組み合わせHの公式と計算方法について解説した後、重複組み合わせの問題をご紹介していきました。

重複組み合わせは◯と|を使いこなせるかがポイントです。ぜひたくさんの問題を解いて重複組み合わせに慣れていきましょう。