皆様は正五角形の内角の和と1つの内角の大きさを自力で求めることはできるでしょうか?
内角および内角の和に関する知識は数学の図形問題を解くにあたって必須の知識となるので、必ず頭に入れておきましょう。
今回は早稲田大学教育学部数学科を卒業した筆者が正五角形の内角の和および1つの内角の大きさを5秒で求める方法について図解でわかりやすく解説していきます。
必ず覚えておかなければいけない内角に関する公式をご紹介するので、ぜひ最後までご覧ください。
正五角形の内角の大きさを5秒で求める方法
正五角形の内角の大きさを5秒で求める方法ですが、多角形の内角の和の公式を使います。
n角形の内角の和は(n-2)×180°で求められるのでした。
※詳しくは内角・外角とは何かについて解説した記事をご覧ください。
今回は正五角形、つまり五角形の内角の和を求めるのでn=5となります。
n=5を上記の公式に代入すると、(5-2)×180°=3×180°=540°となります。
よって、正五角形の内角の和=540°が求まりました。この公式を知っていれば5秒で求まります。
ちなみにですが、正多角形においては1つの内角の大きさはすべて同じです。
なので、正五角形においても5つの内角の大きさはすべて同じです。
したがって、正五角形の1つの内角の大きさ=540°÷5=108°となります。
また、正多角形における外角の大きさもすべて等しく、外角の大きさ=180°-内角で求めることができるので、正五角形の1つの外角の大きさ=180°-108°=72°となります。
正五角形の内角の大きさの求め方2つ目
ここからは、上記の多角形の内角の和の公式を知らない場合の正五角形の内角の和の求め方について解説します。
まずは正五角形ABCDEを書いてみます。
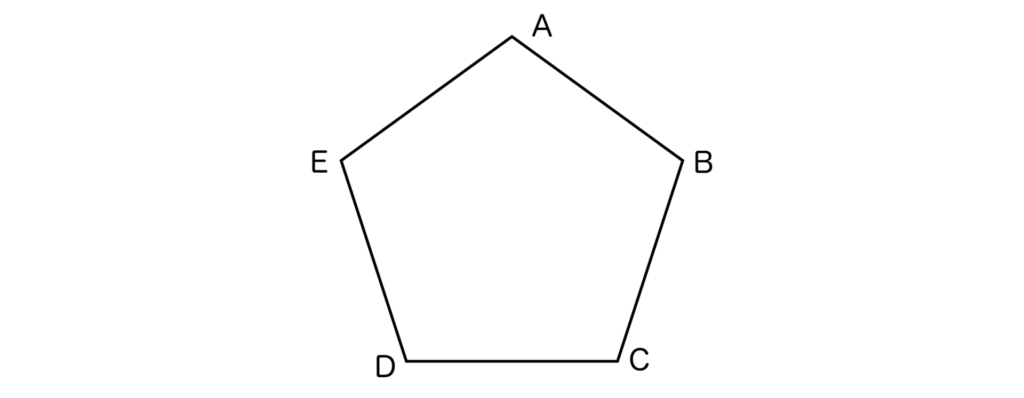
そしてAとC、AとDを結びます。
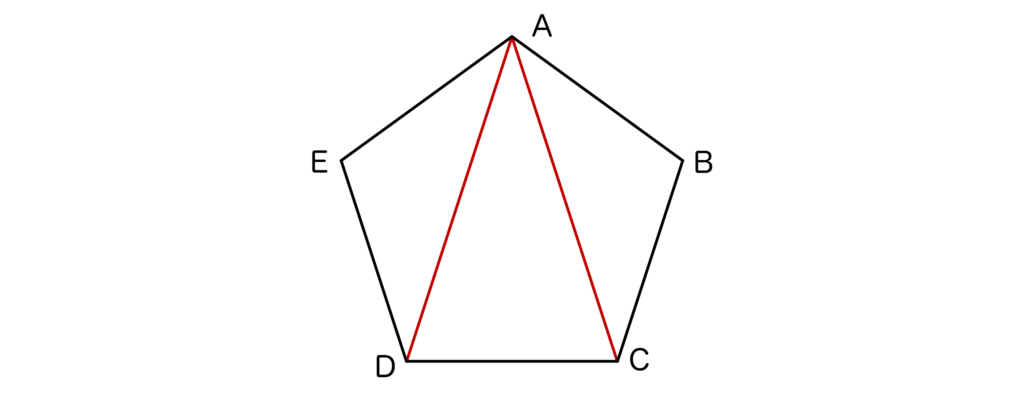
すると、正五角形ABCDEを三角形ABC、ACD、ADEの3つに分割することができました。
ここで、三角形の内角の和は180°でしたね。よって、五角形の内角の和は3×180°=540°となります。
上記でご紹介した多角形の内角の和の公式で正五角形の内角の和を求めたときと同じ結果になっていることが確認できます。
多角形の内角の和の公式を使ったとき、(5-2)×180°=3×180°=540°という計算式になりましたが、この「5-2(=3)」の3は五角形が3つの三角形に分割できるということを意味しています。
一般的に、n角形は(n-2)個の三角形に分解することが可能です。これも多角形の公式の1つとして覚えておきましょう。
正五角形で知っておきたい知識:黄金比
最後に、正五角形で知っておきたい知識として黄金比をご紹介します。
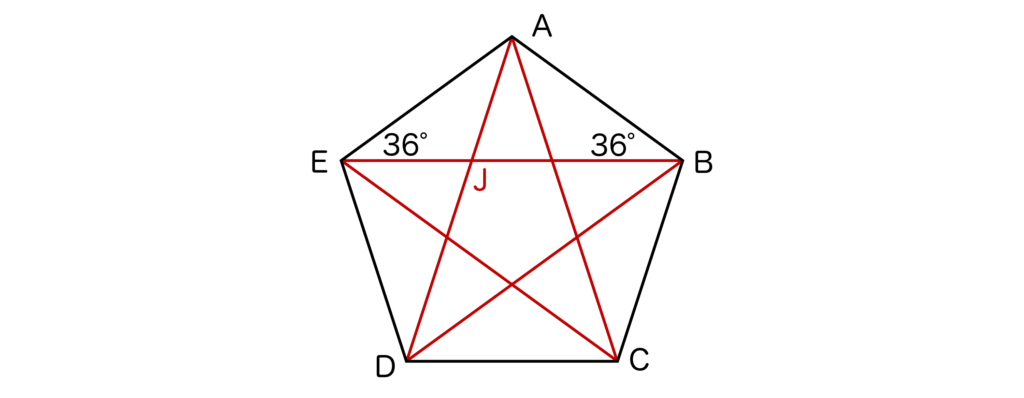
正五角形は以下のように対角線を引くと星形が出来上がります。そして、正五角形の1つの内角の大きさは先ほどの通り108°でした。
三角形ABEに注目すると、三角形ABEはAB=AEの二等辺三角形なので、∠A=108°より、∠AEB=∠ABE=36°になります。
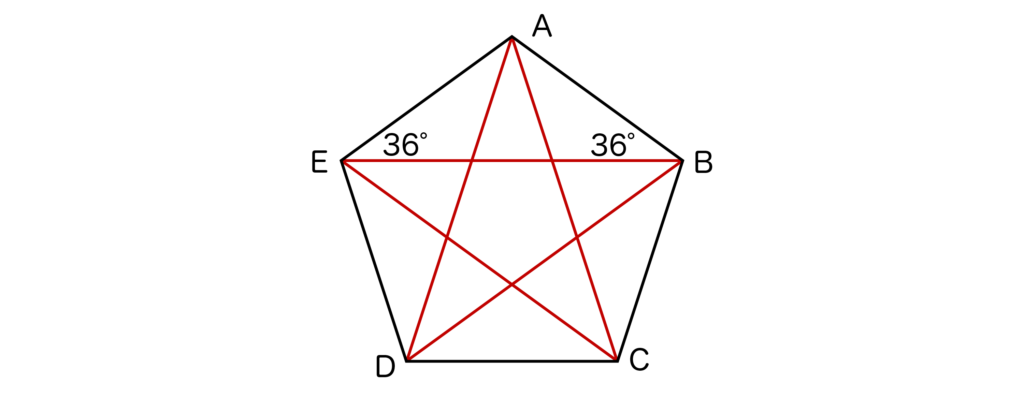
また、三角形EADも二等辺三角形なので∠EAD=∠EAD=36°となります。
ここで、ADとEBの交点をJとします。
すると、三角形ABEと三角形JAEにおいて、
- ∠BEA=∠AEJ=36°
- ∠ABE=∠JAE=36°
より、三角形ABEと三角形JAEは相似となります。
正五角形ABCDEの1辺の長さを1、EJ=xとすると、
AB:BE=JA:AEより、1:(1+x)=x:1となりますね。
※BE=BJ+JEであり、三角形ABJはAB=BJの二等辺三角形なので、BJ=AB=1となります。JE=xなので、BE=1+xとなります。
内項の積=外項の積より、x(1+x)=1・1となるので、x2+x-1=0という二次方程式を作ることができます。
すると、解の公式より、x=(-1±√5)/2となります。
※解の公式がわからない人は二次方程式の解の公式とは何かについて解説した記事をご覧ください。
xはEJの長さであることから、x>0なので、x=(-1+√5)/2となります。
以上より、BE=BJ+JE=1+(-1+√5)/2=(1+√5)/2となることがわかりました。
すると、正五角形ABCDEの1辺の長さ:対角線の長さ=1:(1+√5)/2となりますね。
この比率は黄金比と呼ばれており、自然界や科学・文化など多くの分野に潜んでいる神秘的な比率であることが知られています。
√5≒2.236なので、(1+√5)/2≒1.618です。よって、黄金比はおよそ1:1.618となります。
※√5は「富士山ろくオーム鳴く(2.2360679)」と覚えましょう。その他の語呂合わせについては平方根とは何かについて解説した記事をご覧ください。
黄金比が存在している例としてはiPhoneで有名なAppleのロゴやパルテノン神殿、ハガキ、サグラダ・ファミリアなどがあげられます。

いかがでしたか?
今回は正五角形の内角の大きさを5秒で求める方法と正五角形における黄金比について解説していきました。
黄金比は高校数学における少し応用的な内容ですが、難易度の高い大学を目指している人はぜひ知っておきましょう!
また、五角形だけでなく、六角形の内角の和が720度なのはなぜかについて解説した記事もご用意しているので、ぜひ合わせてご覧ください。