高校数学では有理数という概念が登場しますが、有理数の1つとして循環小数という小数があります。
中学でも登場した循環小数ですが、忘れてしまった人もいるかと思いますので今一度、復習がてら学習しましょう。
本記事では、早稲田大学教育学部数学科を卒業した筆者が循環小数とは何か・循環小数を分数に直す方法などを例題でわかりやすく解説していきます。
循環小数とは?例で解説
循環小数とは小数点以下が循環する小数のことです。
循環とは、ある一定の法則で数字が永遠に繰り返されることです。
例えば、6.149149149…という小数を見てみましょう。
小数点以下の「149」がひたすら(永遠に)繰り返されていますね。よって、この小数は循環小数であると言えます。
循環小数は循環する部分の最初と最後の数字の上に「・」をつけて表現します。
先ほどご紹介した循環小数6.149149…は6.149と表現することができます。
また、循環小数の繰り返す数のことを循環節といい、繰り返す数の長さを循環節の長さといいます。
6.149の場合、循環節は149、循環節の長さは3となります。
循環節の長さについては、「m/nが循環小数で表されるとき、その循環節の長さはn-1以下となる」という法則が成り立ちます。
循環小数を分数に直す方法を例題で解説
循環小数は必ず分数に直すことができます。
例として、0.6を分数に変換してみましょう。
まずは0.6をxとおいてみます。すると、10x=6.6ですね。
よって、10x-x
=6.6-0.6
=6
より、9x=6となるので、x=2/3となります。
2/3を実際に小数に直してみると、2÷3より確かに0.666…となっていることがわかります。
ちなみにですが、0.6の循環節の長さは1ですね。なので、10xを算出しました。
循環節の長さが2の場合は100x、循環節の長さが3の場合は1000xを算出します。
もう1つ例をみてみましょう。循環小数0.389を分数に直してみます。
x=0.389とし、今回は循環節の長さが3なので、1000x=389.389となります。
1000x-x=389より、999x=389となるので、x=389/999となります。
389/999を小数に直すと、389÷999=0.389389…となっていることが確かに確認できます。
循環小数を分数に直す場合は、循環節の長さにぜひ注目してみてください。
循環小数と有理数・無理数の関係
循環小数は有理数の1つとなります。
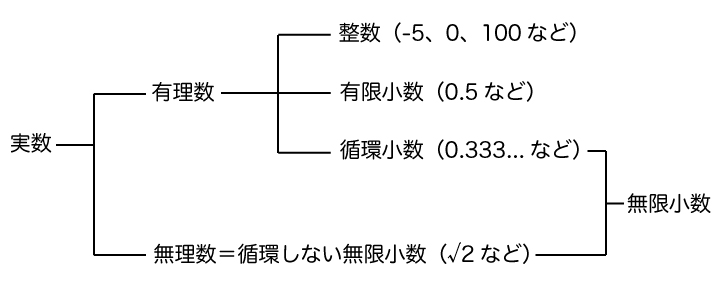
有理数は整数・有限小数・循環小数の3つで構成されています。
※詳しくは有理数とは何かについて簡単に解説した記事をご覧ください。
循環小数と対比されるのは有限小数です。
有限小数とは、循環小数のように小数点以下が永遠に続くことがなく、どこかで途切れる小数のことです。
例えば、0.549、0.5、10.43などです。
一方で、無理数とは小数点以下が法則性を持たずに永遠に続く小数のことです。
例えば、√2は小数に直すと1.414…となり小数点以下は永遠に続きますが、循環小数と違ってそこに法則性は一切ありません。
無理数と循環小数はともに小数点以下が永遠に続くという特徴は同じなので、まとめて無限小数と言われたりもします。
ちなみにですが、有理数と無理数はまとめて実数と言われています。実数とは何かについて解説した記事もぜひ合わせてご覧ください。
循環小数の見つけ方
例えば、1/3という分数があったとき、1/3が循環小数かどうかを見極めるにはシンプルに1÷3を実行して確認すれば良いですが、147/923など、複雑な分数の場合は分子÷分母を行うのが非常に面倒ですね。
そんなとき、その分数が循環小数かどうかを見分ける方法があります。
分母を素因数分解して、2または5以外の素因数が登場したらその分数は循環小数となります。
逆に、分数を素因数分解して、2と5しか登場しない場合、その分数は有限小数となります。
※素因数分解=ある正の整数を素数のみの掛け算で表すこと。例えば、70を素因数分解すると、2×5×7となります。詳しくは素因数分解とは何かについて解説した記事をご覧ください。
例として、1/15を考えてみましょう。15を素因数分解すると3×5となり5が含まれていますが、2と5以外の数字である3も登場しているので循環小数となります。
実際に1/15を小数に変換してみると、0.06666…となるので循環小数になっていることがわかります。
では、1/250はどうでしょうか?250を素因数分解すると2×53となり、2と5以外の数字は登場しません。
よって、1/250は有限小数となります。実際に1/250を小数に変換してみると0.004となり、確かに循環小数ではないことがわかります。
分母を素因数分解して2と5以外の数字が出るか?で循環小数かどうかを判別するテクニックはかなり使えますので、ぜひ覚えておきましょう。
循環小数の練習問題
最後に、循環小数の練習問題をご紹介します。
すべて基本的な問題なので、全問正解できるようにしておきましょう。
【練習問題1】
以下の分数を小数に直し、循環小数の表し方で書きなさい。
(1)5/9
(2)31/30
【解答&解説】
(1)5÷9=0.5555…より、0.5・・・(答)
(2)31÷30=1.0333…より、1.03・・・(答)
【練習問題2】
以下の循環小数を分数に直しなさい。
(1)0.7
(2)0.729
【解答&解説】
(1)x=0.7とおきます。すると、10x=7.7より、10x-x=7となるので、x=7/9・・・(答)となります。
※7÷9は確かに0.777…となっています。
(2)x=0.729とおきます。循環節の長さが3なので、1000xを考えましょう。
1000x=729.729ですね。
よって、1000x-x=729より、x=729/999・・・(答)となります。
※729÷999は確かに0.729729…となっています。
今回は循環小数とは何かについて解説した後、循環小数を分数に直す方法、循環小数と有理数・無理数の関係、循環小数の見つけ方について解説しました。
循環小数を分数に直す問題は共通テストでもたまに出題されますので、必ずできるようにしておきましょう!