本記事では実数の1つである有理数について深く解説していきます。
後ほど詳しく解説しますが、有理数は分数で表現できるという大きな特徴があり、高校数学では必須の知識となっています。
そこで今回は早稲田大学教育学部数学科を卒業し、数学に関して深い知見のある筆者が有理数とは何かについて簡単に解説した後、0は有理数か?などよくある疑問についても回答していきます。
有理数とは?例で簡単に解説
まずは有理数とは何か・定義について例を使いながら簡単に解説します。
有理数とは、整数mと0ではない整数nを用いて分数m/nで表現できる数のことを言います。
つまり、簡単に言うと分数で表現できる数=有理数ということです。
そして、有理数(=分数で表現できる数)には以下3つがあります。
- 整数
- 有限小数
- 循環小数
それぞれ順番に詳しく解説していきます。
整数
整数とは、自然数(1、2、3、4・・・)に0と-1、-2、-3、-4・・・を合わせた数のことです。
3.5や-90.8などの小数や1/5、-1/100などの分数は整数ではありません。
整数は必ず分数で表現できます。例えば、5=5/1ですし、-30=-30/1です。0は0/nで表現できます。
2つの整数の和・差・積は常に整数となります。
しかし、商は整数とは限りません。例えば、10÷4=2.5なので、商が整数ではなく小数になっています。
有限小数
有限小数とは、小数点以下が有限である(=永遠に続くことがない)小数のことです。
例えば、0.5や6.932、-10.56などです。
また、1/2=0.5で小数点以下が有限なので有限小数とも言えます。1/10や1/5も同様です。
有限小数は必ず分数で表現できます。
例えば、0.453=453/1000ですし、-9.3=-93/10です。
循環小数
循環小数は有限小数と違い、小数点以下が循環する(=法則性を持って永遠に続く)小数のことです。
例えば、1/3=0.3333…となり3が永遠に続くので循環小数と言えます。
3/7=0.428571428571…となり、小数点以下は「428571」が永遠に続くので循環小数となります。
循環小数は循環する部分の最初と最後の数字の上に・印をつけて表現します。
例えば、先ほどご紹介した1/3=0.333…の場合は0.3となります。
0.428571428571…の場合は0.428571となります。
循環小数も必ず分数で表現することが可能です。循環小数を分数に変換する方法は中学数学で学習したかと思いますが、念のためおさらいしておきます。
例えば、循環小数0.67を分数に変換してみます。
x=0.67とします。すると、100x=67.67ですね。
すると、100x-x=67より、99x=67となるのでx=67/99となります。
実際に67÷99=0.67となっていることがわかります。
※循環小数について詳しく解説した記事もぜひ合わせてご覧ください。
以上が有理数(整数・有限小数・循環小数)に関する解説となります。
ちなみにですが、2つの有理数の和・差・積・商は必ず有理数となるということも一緒に覚えておきましょう。
また、これは余談ですが、有理数はローマ字のQで表現することが可能です。
Qは英語で和・差・積・商の「商」を意味するQuotientの頭文字を取ったものです。
5∈Qのように表記することで「5はQ(有理数)に含まれる」と表現することが可能です。
有理数と無理数の違い・見分け方は?
有理数と対比される用語として、無理数があります。
無理数とは、小数点以下が法則性を持たずに永遠に続く小数のことです。
例えば、円周率のπ=3.141565…と小数点以下が永遠に続きますが、循環小数のように法則性はありません。
また、√3=1.732…とこれも小数点以下が永遠に続きますが、循環小数のように法則性はありません。
以上のような数のことを無理数と言います。
ちなみに、無理数と有理数の循環小数を合わせて無限小数と言うので覚えておきましょう。
無理数は有理数と違って分数で表現することができません。なので、有理数と無理数の見分け方としては
- 分数で表現できるか
- 小数の場合、小数点以下が循環するか
がポイントになります。
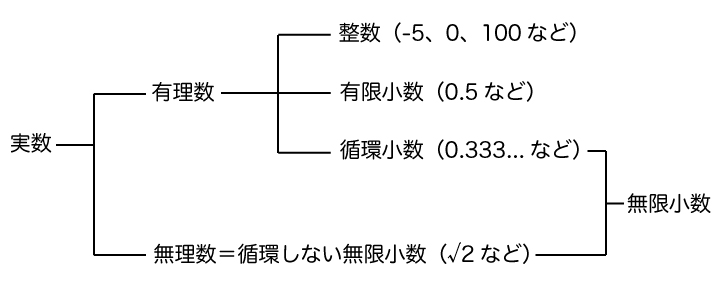
また、有理数と無理数を合わせて実数と呼ぶのでこれも覚えておきましょう。
※実数とは何かについて詳しく解説した記事もぜひ合わせてご覧ください。
以上をまとめると以下のようになります。
0やルートは有理数?よくある疑問
最後に、有理数・無理数に関してよくある質問をまとめておきます。
忘れてしまったときにぜひ見返してください。
【Q】0は有理数ですか?
【A】はい、有理数です。0は整数の1つであるため、有理数となります。自然数ではないのでご注意ください。自然数は1以上の整数を指しています。
【Q】ルートがつく数は無理数ですか?
【A】必ず無理数とは言えません。有理数となる場合もあります。例えば、√7=2.6457…なので無理数ですが、√4=2なので有理数となります。
【Q】マイナスの数は有理数ですか?
【A】必ず有理数とは言えません。無理数となる場合もあります。例えば、-10は有理数ですが、-√2=-1.414…なので無理数となります。有理数・無理数の見分けは符号で判断するのではなく、分数で表現できるかどうかで判断するようにしましょう。
今回は有理数とは何か・定義について解説した後、有理数の種類(整数・有限小数・循環小数)や無理数との違い、有理数に関するよくある質問をご紹介しました。
有理数は高校数学でも基礎的な内容の1つなので、しっかりと中身を理解するようにしておきましょう。


