比や比の値は小学校でも学習した内容ではありますが、中学数学でも再び登場していきます。
比や比の値は数学の基礎ともいえる内容なので、必ず頭に入れておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者が比の値とは何かについて解説した後、比の値の求め方を例題でわかりやすく解説していきます。
また、比に分数や小数が含まれる場合の比の値の求め方も解説していきます。
数学が苦手な人でも理解できるように解説していくので、ぜひ最後までご覧ください。
比の値とは?求め方は?
では早速、比の値とは何か・求め方について解説します。
比の値とは、比a:bにおいてa/bのことをいいます。
a:bの比の値はaがbの何倍になっているかを表しています。
例えば、4:5の比の値は4/5となります。4は5の4/5倍(=0.8倍)であることがわかります。
比の値の求め方はとても簡単ですね。
※ちなみにですが、a:bの比の値とc:dの比の値が等しいとき、a:b=c:dと表し、この式のことを比例式といいます。比例式とは何かについて解説した記事もぜひ合わせてご覧ください。
では、練習として以下の比の値を求めてみましょう。
【問題】
以下の比における比の値を求めなさい。
(1)1:2
(2)3:8
(3)5:9
(4)4:8
(5)6:9
【解答&解説】
(1)1:2の比の値=1/2
(2)3:8の比の値=3/8
(3)5:9の比の値=5/9
(4)4:8の比の値=4/8=1/2
※4:8=1:2に直してから比の値1/2を求めても問題ありません。
(5)6:9の比の値=6/9=2/3
※6:9=2:3に直してから比の値2/3を求めても問題ありません。
比の値を求めるときは約分も忘れないようにしましょう。
比が分数のときの比の値の求め方
では、4/5:7/10のように比に分数が含まれている場合の比の値はどうやって求めれば良いのでしょうか?
こちらも簡単なのでご安心ください。
先ほども解説した通り、a:bの比の値=a/bでした。a/b=a÷bのことですね。
※割り算のことを中学数学では除法というのでした。除法とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。
なので、4/5:7/10の比の値は4/5 ÷ 7/10=4/5 × 10/7=8/7・・・①となります。
※割り算は逆数を使って掛け算に変換できるのでしたね。
もしくは4/5:7/10の比を整数の比にしてから比の値を求めても問題ありません。
4/5:7/10は両方に10をかけることによって、8:7になりますね。
よって、8:7の比の値=8/7となります。確かに①の値と一致していることがわかります。
比が小数のときの比の値の求め方
比が小数のときの比の値の求め方も分数のときと考え方は同じです。
例として0.5:0.8の比の値を求めてみましょう。
a:bの比の値=a/bなので、0.5:0.8の比の値=0.5/0.8=5/8・・・②となります。
別の求め方もご紹介しておきます。0.5:0.8は両方に10をかけることで5:8とすることができますね。
よって、5:8の比の値=5/8となります。確かに②の値と一致していることがわかります。
比が小数の場合は先に比を整数の比に変換してから比の値を求める方が楽なケースが多いです。
比の値を求める計算機
比の値の求め方が完璧になれば、自力で比の値を求めるのが面倒に感じる場合もあるでしょう。
そんな人のために念のため、比の値を求めることができる計算機をご紹介しておきます。それは「算数の電卓」という計算機です。
使い方ですが、今回は15468:329530の比の値を求めるとします。自力で求めるのはちょっと大変そうですね。
まず、「算数の電卓」にアクセスします。すると、以下のような画面が登場します。
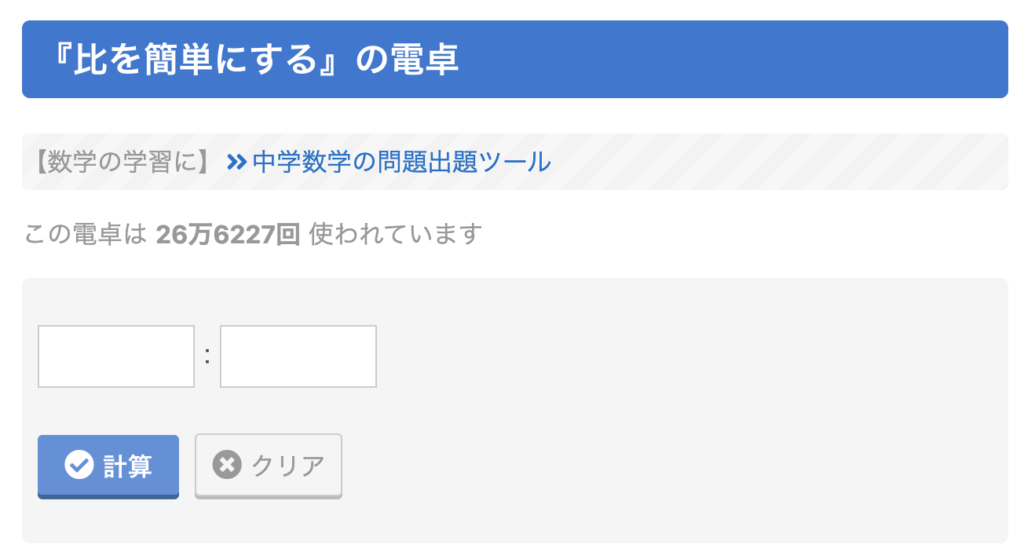
そして、2つの空欄に15468と329530を入力して「計算」ボタンをクリックします。すると、以下のような画面になります。
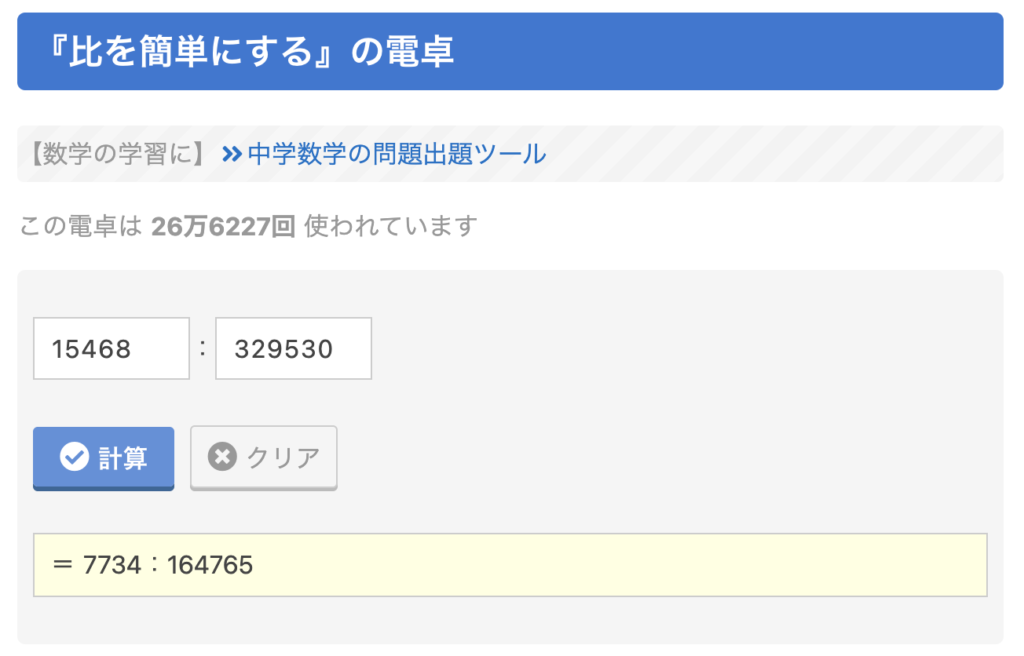
これで15468:329530=7734:164765になることがわかりました。
したがって15468:329530の比の値=7734/164765となります。
以上の計算機を使えばどんな複雑な比の値でも一発で求めることができます。ぜひ機会があれば使ってみてください。
比の値の練習問題
最後に比の値の練習問題をご用意しました。
すべて上記で学習した内容なので、必ず解けるまで比の値とは何かを理解しましょう。
【練習問題】
以下の比における比の値を求めよ。
(1)6:16
(2)4/9:5/6
(3)6/10:4/90
(4)1.6:2.8
(5)1.84:4.2
【解答&解説】
(1)6:16=3:8なので、比の値=3/8
(2)4/9:5/6=8:15なので、比の値=8/15
(3)6/10:4/90=27:2なので、比の値=27/2
(4)1.6:2.8=16:28=4:7なので、比の値=4/7
(5)1.84:4.2=184:420=46:105なので、比の値=46/105
いかがでしたでしょうか?
今回は比の値とは何か?求め方について解説しました。
分数や小数が登場したときも決して慌てず、a:bのa、b両方に数字をかけて整数の比に直すことを心がけてください。