二次不等式では解=全ての実数となるケースがあります。
しかし、全ての実数が解になるとはどういうことか理解できていない人も多いのではないでしょうか?
そこで今回は早稲田大学教育学部数学科を卒業した筆者が二次不等式における全ての実数とは何か?について解説した後、解=全ての実数となる場合を全てご紹介していきます。
数学が苦手な人でも二次不等式の全ての実数とは何かが理解できるように解説していくので、ぜひ参考にしてください。
※二次不等式の解き方について解説した記事もぜひ参考にしてください。
二次不等式における全ての実数とは?
まずは全ての実数とは何かについて解説していきます。
実数とは有理数と無理数を合わせた数のことを言います。実数の反対は虚数です。
虚数は「i」という記号を使って表記され、i2=-1となります。
※虚数の例=4i、-9iなど
つまり、虚数以外の数字は全て実数です。なので、実数とは超簡単にいうと普段目にする全ての数字のことです(虚数は普段目にすることはありませんね)
なので、二次不等式において「全ての実数」という言葉が出てきたら「全ての数」と認識しておけば一旦はOKです。もちろん0やルート、マイナスの数なども全て実数となります。
実数についてもっと深く知りたい人は実数とは何かについて解説した記事をご覧ください。
二次不等式で解=全ての実数になるケース
二次不等式で解=全ての実数になるケースは以下の4通りです。
a>0かつ判別式D=0のとき、二次方程式ax2+bx+c=0の重解=αとすると、
- ax2+bx+c≧0の解=全ての実数
- (x-α)2≧0の解=全ての実数
また、a>0かつ判別式D<0のとき、
- ax2+bx+c>0の解=全ての実数
- ax2+bx+c≧0の解=全ての実数
順番に解説していきます。
ax^2+bx+c≧0の解=全ての実数
まずa>0かつ判別式D=0で重解=αということは、二次関数y=ax2+bx+cをグラフにしてみると以下のようになりますね。
※判別式とは何かについて解説した記事や重解とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。
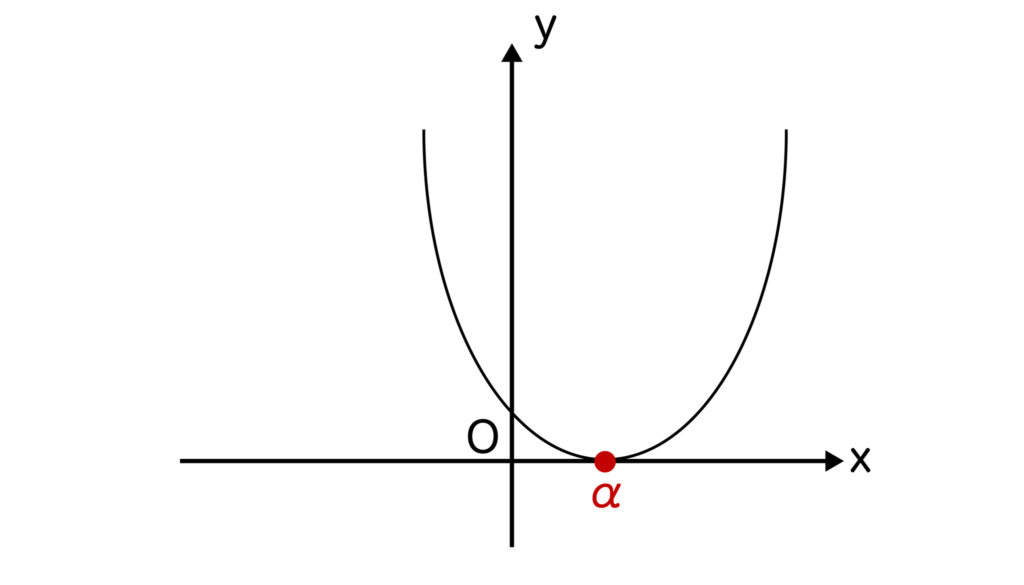
a>0より、y=ax2+bx+cのグラフは下に凸なグラフとなります。
そして、重解=αを持つということはx=αの1点でx軸と接するということです。
※グラフの書き方がわからない人は二次関数のグラフの作成方法について解説した記事をご覧ください。
ここで、改めてax2+bx+c≧0を考えてみましょう。
ax2+bx+c≧0ということはy≧0ということです。グラフを見て、y≧0になっているところはどこかを探しましょう。
すると、xがどんな値を取ろうともyは必ずy≧0になっていることがわかりますね。したがって、ax2+bx+c≧0の解は全ての実数となるのです。
(x-α)^2≧0の解=全ての実数
先ほど、a>0かつ判別式D=0のとき、二次方程式ax2+bx+c=0の重解=αとするという記載がありました。
つまり、ax2+bx+cを因数分解すると(x-α)2になるということですね。
※数学1の因数分解について解説した記事もご用意していますので、ぜひ参考にしてください。
なので、(x-α)2≧0は先ほどのax2+bx+c≧0と同じ意味なのです。
したがって、(x-α)2≧0の解は先ほどと同様に全ての実数となります。
ax^2+bx+c>0の解=全ての実数
今度は二次方程式ax2+bx+c=0において、a>0かつ判別式D<0のときです。
二次関数y=ax2+bx+cのグラフを書いてみると、以下のようになりますね。
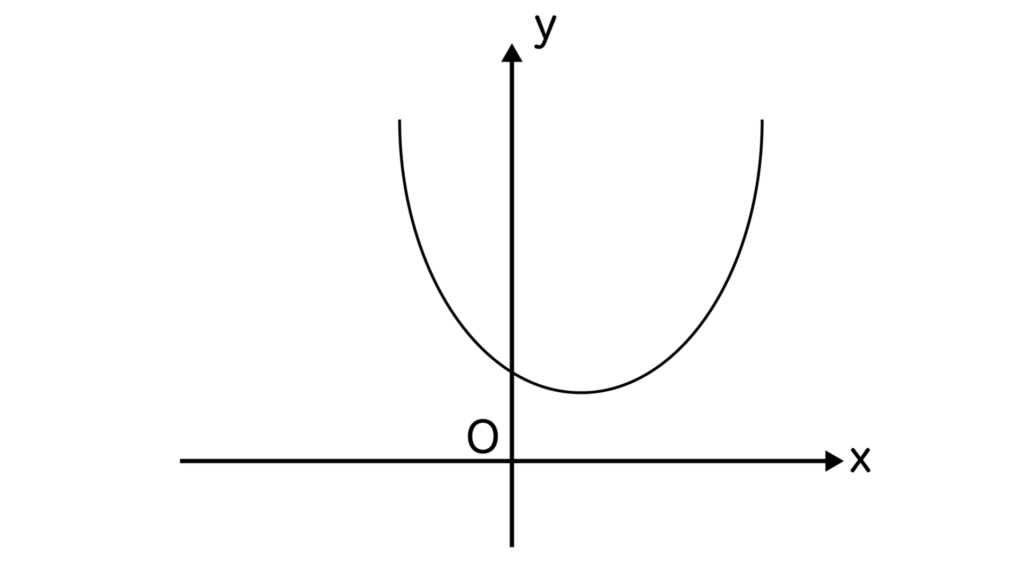
a>0なので下に凸なグラフとなります。また、判別式D<0より二次関数y=ax2+bx+cはx軸と接点を持ちません。
このような状況において、ax2+bx+c>0つまりy>0となっている箇所を探してみましょう。
こちらもxがどんな値を取ろうともyは必ずy>0になっていることがわかりますね。
よって、ax2+bx+c>0の解は全ての実数となるわけです。
ax^2+bx+c≧0の解=全ての実数
では、ax2+bx+c≧0の場合はどうでしょうか?
上記のグラフより、ax2+bx+c=0となる場合はありませんが、0以上であることは確かですね。
よって、ax2+bx+c≧0の解もax2+bx+c>0の解と同様に全ての実数となります。
いかがでしたか?今回は二次不等式における全ての実数とは何かについて解説した後、解=全ての実数になるパターンもご紹介していきました。
迷った時は二次関数のグラフを書くということをぜひ意識してみてください。


