二次方程式の解の公式とは？証明や覚え方も紹介！計数が偶数のときは？

二次方程式で最も重要な公式の1つが解の公式です。大学入試や共通テストでは必ずと言って良いほど頻出の公式となりますので必ず覚えなくてはなりません。

そこで今回は、早稲田大学教育学部数学科を卒業した筆者が二次方程式の解の公式をご紹介した後、解の公式が成り立つことの証明や覚え方もご紹介します。

また、二次方程式ax²+bx+c=0において、bが偶数であるときの解の公式についても解説します。ぜひ最後までお読みください。

※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。

二次方程式の解の公式とは？

二次方程式ax²+bx+c=0があるとき（a、b、cは実数でaは0でないとする）、その解はb²-4ac≧0のとき、x=-b±√（b²-4ac） / 2aとなります。

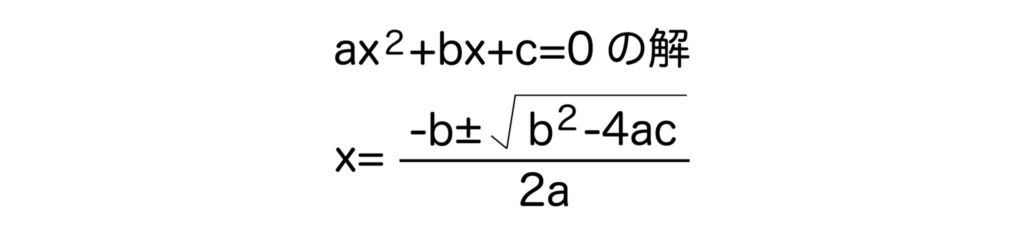
これを解の公式と呼びます。

※実数がわからない人は実数とは何かについて解説した記事をご覧ください。

解の公式は中学数学でも学習しますが、大学入試や共通テストでも登場します。二次方程式における最重要公式と言っても過言ではないので、必ず覚えておきましょう。

特に、b²-4acは判別式と呼ばれており、Dで表現されます（D=b²-4ac）

判別式については以下が成り立ちますので、これも必ず覚えておきましょう。判別式について詳しく解説した記事もぜひ参考にしてください。

• D>0 ⇔ 異なる2つの実数解を持つ
• D=0 ⇔ ただ1つの実数解を持つ（重解と言います。重解について詳しく解説した記事もぜひ参考にしてください。）
• D<0 ⇔ 実数解を持たない

※記号「⇔」の意味がわからない人は必要条件・十分条件について解説した記事をご覧ください。

例えば、解の公式を使ってx²+6x+8=0を解いてみましょう。

a=1、b=6、c=8なので、

x = -6±√（6²-4×1×8） / 2×1 = -6±√4 / 2 = -2、-4・・・（答）となります。

ちなみに、x2+6x+8を因数分解すると（x+2）（x+4）となるので、確かにx=-2、-4となることがわかります。

※因数分解がわからない人は数学1の因数分解について解説した記事をご覧ください。

二次方程式の解の公式の覚え方

二次方程式の解の公式は少し長いので、覚えにくいと感じている人も多いでしょう。

覚え方ですが、残念ながら覚えやすい語呂合わせなどもないので、x=-b±√（b²-4ac） / 2aを念仏のように唱えるしかないのですが、効果がある方法としては解の公式x=-b±√（b²-4ac） / 2aを紙に書いて、それをトイレの壁に貼り付けることです。

おそらく1〜2週間もあれば完璧に覚えられるでしょう。

冒頭でも述べた通り、筆者は早稲田大学教育学部数学科に入学したのですが、高校生のときは覚えにくい公式などはこの方法を使っていました。

非常に効果のある覚え方なので、ぜひ試してみてください。

二次方程式の解の公式の証明

ここからは解の公式が成り立つことの証明を行っていきます。

結論としては、ax²+bx+cを平方完成するだけです。

※平方完成がわからない人は、平方完成の公式・やり方について解説した記事をご覧ください。

（証明）

ax²+bx+c=0より、a（x+b/2a）²-（b²-4ac）/4a=0

よって、（x+b/2a）²=（b²-4ac）/4a²・・・①

b²-4ac≧0のとき、（b²-4ac）/4a²≧0から

x+b/2a = ±√（b²-4ac）/4a²・・・②

※①から②の変形がわからない人は平方根の計算方法について解説した記事をご覧ください。

ここで、

a>0のとき、√4a²=2a

a<0のとき、√4a²=-2a

よってaの正負に関係なくx+b/2a=±√（b²-4ac）/2aとなる。

したがって、x = -b/2a±√（b²-4ac）/2a = -b±√（b²-4ac）/2aとなる（証明終）

xの係数が偶数のときの解の公式と証明

二次方程式ax²+bx+c=0において、xの係数が偶数の場合は少し楽に解を求めることが可能になります。

※係数の意味がわからない場合は多項式の定義について解説した記事をご覧ください。

b=2b’ならば、x=-b’±√（b’²-ac） / aとなります。

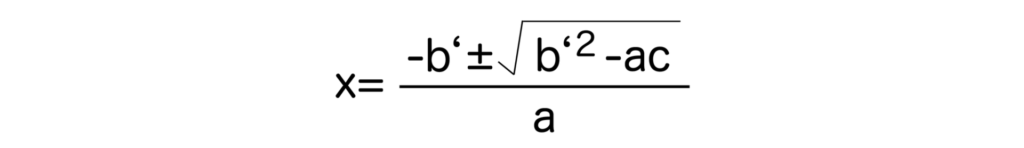
証明ですが、b=2b’のとき√（b²-4ac）＝√4（b’²-ac）=2√（b’²-ac）となるので、

x = -2b’±2√（b’²-ac）/2a = -b’±√（b’²-ac）/aとなります。

例として、二次方程式x²+10x+24=0を解いてみましょう。

a=1、b’=5、c=24なので、

x=-5±√（5²-1×24） / 1 = -5±√1 = -6、-4・・・（答）となります。

二次方程式の解の公式を使った練習問題

二次方程式の解の公式に関する解説は以上となります。

ここからは二次方程式の解の公式を使った練習問題をご用意しています。

以下の練習問題以外にもなるべく多くの問題を解いて、解の公式に慣れていきましょう。

【練習問題】

以下の二次方程式を解の公式を使って解きなさい。

（1）x²+7x+12=0

（2）2x²+14x+20=0

（3）15x²-4x-4=0

【解答＆解説】

（1）x²+7x+12より、a=1、b=7、c=12となるので、

x=-7±√（7²-4×1×12） / 2×1 = -7±√1 / 2 = -4、-3・・・（答）

（2）2x²+x-14x+20より、a=2、b=14、c=20となるので、

x=-14±√(14²-4×2×20) / 2×2 = -14±√36 / 4 = -2、-5・・・（答）

（3）今回はxの係数が-4で偶数なので、b’=-2で解の公式を使いましょう。

a=15、b’=-2、c=-4より、

x=-（-2）±√{（-2）²-15×（-4）} / 15 = 2±√64 / 15 = 2/3、-2/5・・・（答）

今回は二次方程式の解の公式のご紹介と覚え方・証明について解説しました。

解の公式は覚えておかないと大学入試や共通テストで歯が立たなくなります。必ず覚えておきましょう。