二次方程式とグラフの関係を図解でわかりやすく解説！

二次方程式とグラフの関係性は理解できていますでしょうか？

後ほど詳しく解説しますが、二次方程式の解＝グラフにおけるx軸との交点のx座標になります。

本記事では早稲田大学教育学部数学科を卒業した筆者が二次方程式とグラフの関係について図解でわかりやすく解説していきます。

数学が苦手な人でも理解できるようにわかりやすく解説していきますので、ぜひ最後までお読みください。

※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。

二次方程式とグラフの関係

では早速、二次方程式とグラフの関係について解説していきます。

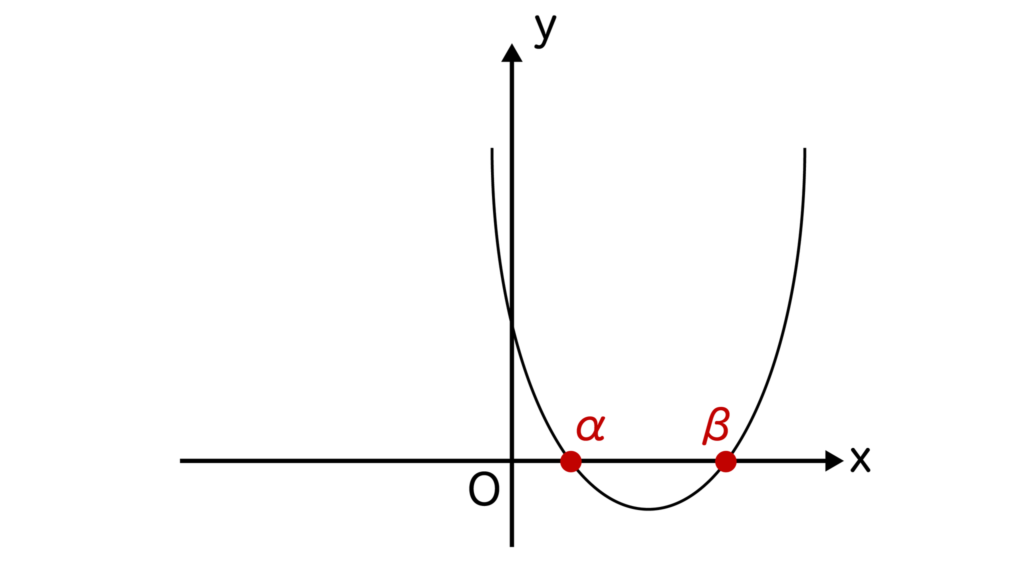
二次方程式ax²+bx+c=0があったとき、この二次方程式の解をα、βとします。

このとき、αとβは二次関数y=ax²+bx+cのx軸との交点のx座標になります。

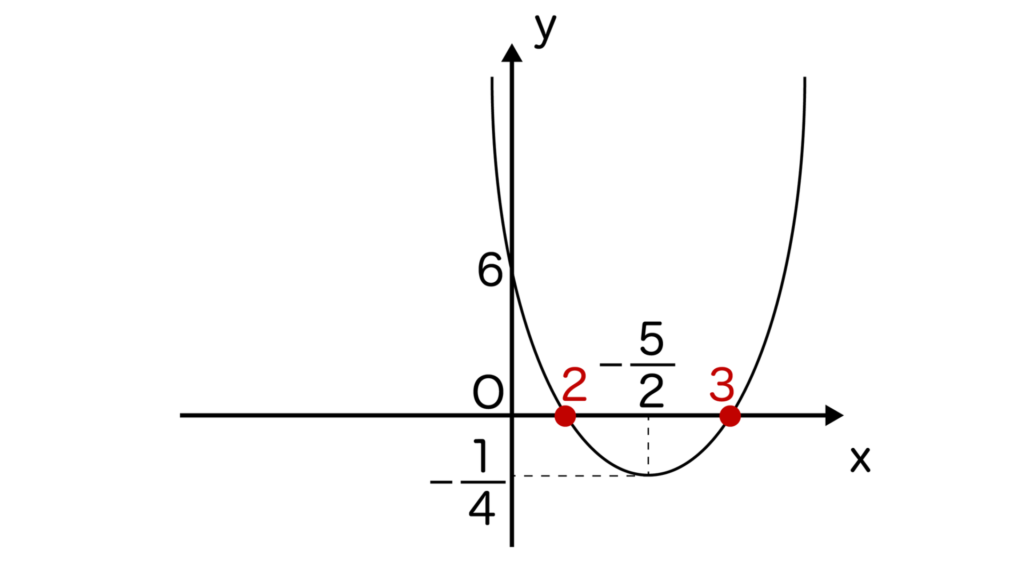
例えば、二次方程式x²-5x+6=0を考えてみましょう。

x²-5x+6を因数分解すると（x-2）（x-3）となるので、x=2、3となりますね。

※因数分解のやり方がわからない人は、数学1の因数分解について解説した記事をご覧ください。

ここで、二次関数y=x²-5x+6をグラフにしてみると以下のようになるので、x軸との交点は（2、0）と（3、0）であることがわかりますね。確かにx=2、3となっていることがわかります。

以上が成り立つ理由ですが、二次方程式x²-5x+6=0においてy=x²-5x+6とすると二次方程式はy=0と表すことができますね。

y=0は二次関数のグラフでいうところのx軸に該当するので、二次方程式x²-5x+6=0の解はグラフにすると二次関数y=x²-5x+6のx軸との交点のx座標になるというわけです。

先ほどはx²の係数がプラスでしたので下に凸なグラフとなりましたが、x²の係数がマイナスのときはどうなるでしょうか？

※係数の意味がわからない人は多項式の定義について解説した記事をご覧ください。

二次方程式-x²+8x-12=0で考えてみましょう。

-x²+8x-12=0を解くために、両辺にマイナス1をかけます。

すると、x²-8x+12=0となりますね。x²-8x+12を因数分解すると（x-2）（x-6）となるので、x=2、6となります。

ここで、y=-x²+8x-12とするとグラフは以下のようになりますね。

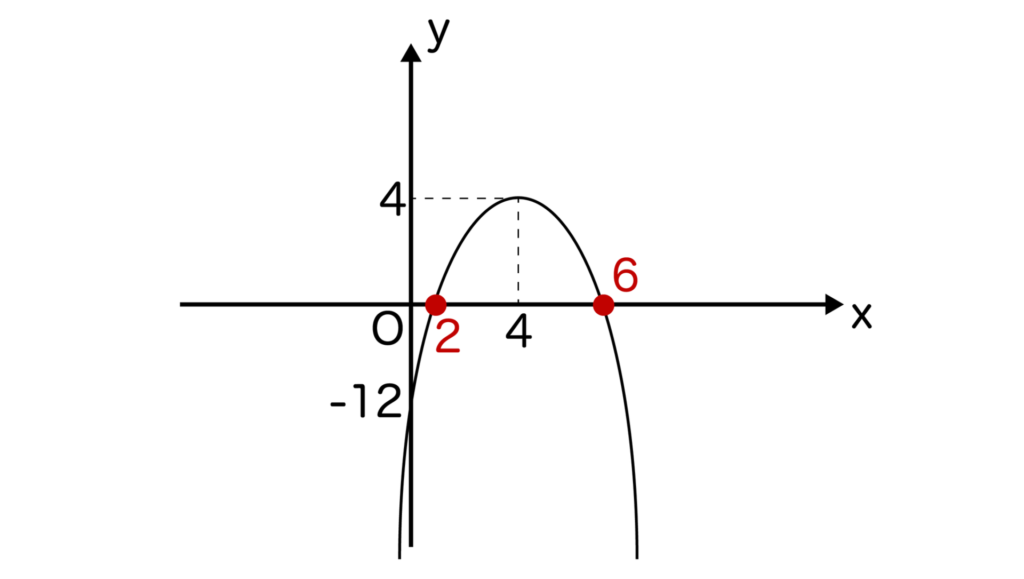
x軸との交点が確かに（2、0）と（6、0）になっていることが確認できます。y=-x²+8x-12なので、上に凸なグラフになっていることも注意しましょう。

二次方程式を平方根を使って解く方法を解説した記事をご覧いただくとわかりますが、二次方程式は平方完成を利用して解くことも可能です。

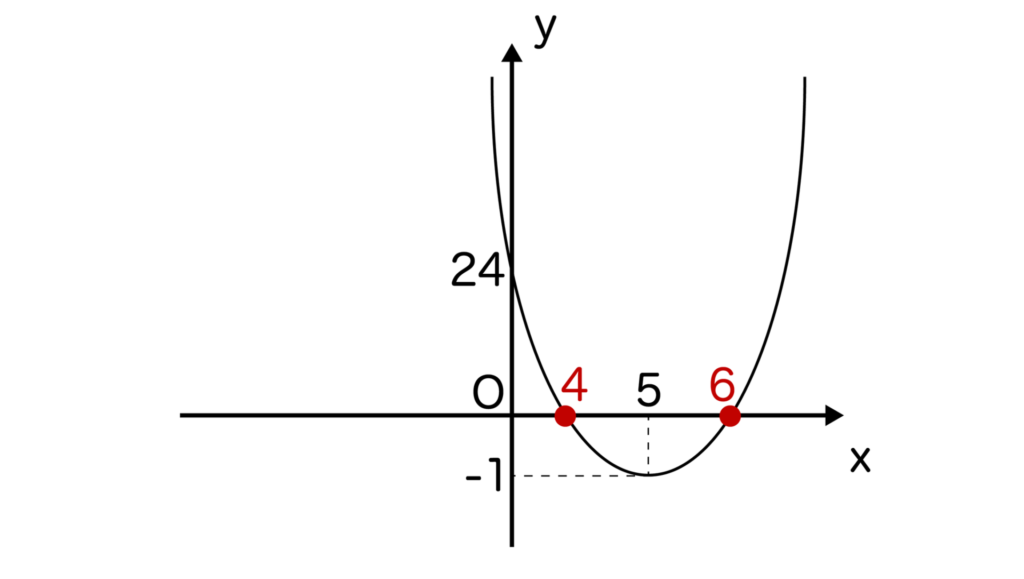
例えばx²-10x+24=0を平方完成を利用して解いてみましょう。

x²-10x+24を平方完成すると（x-5）²-1となりますね。

※平方完成のやり方について解説した記事もご用意しているので、ぜひ合わせてご覧ください。

すると（x-5）²-1=0より、（x-5）²=1となるのでx-5=±1となります。

したがってx=4、6となります。

x²-10x+24を平方完成した形は上記の通り（x-5）²-1となっており、これによって二次関数y=x²-10x+24の頂点の座標を求めることができますね。

※頂点の座標は（5、-1）となります。詳しくは二次関数の頂点について解説した記事をご覧下さい。

y=x²-10x+24をグラフにすると以下のようになり、確かにx軸と（4、0）と（6、0）で交わり、頂点の座標は（5、-1）であることが確認できます。

いかがでしたでしょうか？今回は二次方程式とグラフの関係について解説しました。

二次方程式ax²+bx+c=0の解は二次関数y=ax²+bx+cのx軸との交点のx座標であることを理解しておきましょう。