二次方程式の解き方としては因数分解・平方完成・解の公式の3つがありますが、今回はその中でも因数分解に焦点を当てます。
因数分解を使って二次方程式を解くというのは王道の方法となります。
本記事では早稲田大学教育学部数学科を卒業した筆者が二次方程式を因数分解を使って解く方法についてパターン別にわかりやすく解説していきます。
また、二次方程式が因数分解できないときはどうすれば良いのか?についても解説していきます。
※二次方程式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式を因数分解で解く(超基本編)
二次方程式とは、最高次数が2である方程式のことなのでx2=49も立派な二次方程式となります。
※次数がわからない人は多項式の定義について解説した記事をご覧ください。
xを2回かけて49になる数字は-7と7なので、x=-7、7となります。
つまり、上記では49の平方根を求めたことになります。
一般的に、正の整数aの平方根は√aと-√aになるので超基本事項として覚えておきましょう。
平方根とは何かについて詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
二次方程式を因数分解で解く(xでくくる)
二次方程式x2+x=0を解いてみましょう。
x2+xをxでくくるとx(x+1)となるので、x(x+1)=0となりますね。
2つの数を掛け合わせて0になるということは、x=0またはx+1=0ということになります。
したがって答えはx=0、-1となります。
xでくくるというのも立派な因数分解なので、必ずできるようにしておきましょう。
二次方程式を因数分解で解く(2乗の形)
二次方程式x2+16x+64=0を解いてみましょう。
x2+16x+64を因数分解すると(x+8)2となるので、(x+8)2=0となります。
よって、x+8となるのでx=-8が求まります。
因数分解において2乗の形は頻出なので、必ず以下の公式を覚えておきましょう。
- a2+2ab+b2 = (a+b)2
- a2-2ab+b2 = (a-b)2
二次方程式を因数分解で解く(右辺を移行)
今度は二次方程式x2+10x=-25を解いてみましょう。
二次方程式を解くには、右辺を0にしてから解かなければなりません。
今回は右辺が-25なので、これを左辺に移行させましょう。
右辺の-25を左辺に移行すると、x2+10x+25=0となり、右辺を0にすることができました。
x2+10x+25を因数分解すると(x+5)2なので、答えはx=-5となります。
二次方程式では、右辺は必ず0にするということを必ず覚えておきましょう。
二次方程式を因数分解で解く(たすき掛け)
最後はたすき掛けです。因数分解で最も有名なテクニックです。
二次方程式2x2+9x+4=0を解いてみましょう。
2x2+9x+4を因数分解すると(2x+1)(x+4)となります。たすき掛けの図を書くと以下の通りとなります。
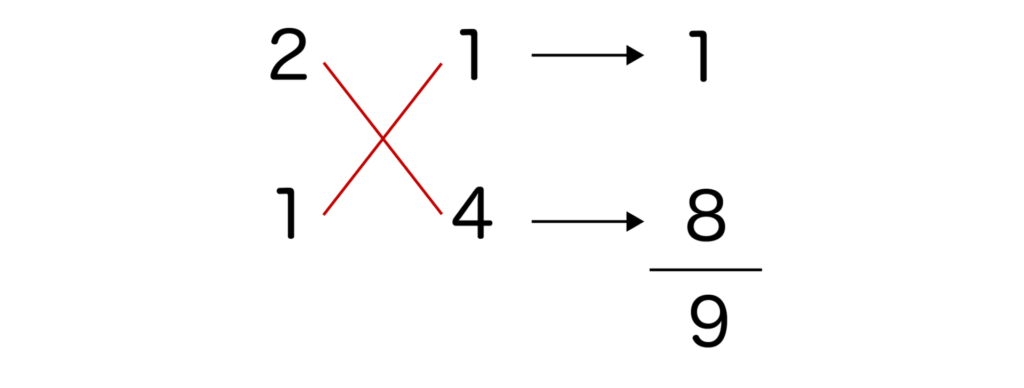
たすき掛けのやり方がわからない人は数学1の因数分解について解説した記事をご覧ください。
よって答えはx=-1/2、-4となります。
二次方程式を解くために因数分解のたすき掛けの知識は必須ですので、必ずできるようにしておきましょう。
二次方程式を因数分解で解く(x以外の文字)
二次方程式では未知数が必ずしもxとは限りません。x以外の文字が使われることもあります。
しかし、解き方は未知数がxのときと何1つ変わりませんので、そこはご安心ください。
【例題】
二次方程式a2-10a+16=0を解きなさい。
【解答&解説】
今回はxではなくaという文字になっています。
a2-10a+16を因数分解すると(a-2)(a-8)となるので、答えはa=2、8となります。
x=2、8ではありませんのでご注意ください。
二次方程式が因数分解できないとき
では、与えられた二次方程式が因数分解できないときはどうやって解けば良いのでしょうか?
結論としては平方完成か解の公式を使うことになります。
例えば、二次方程式x2+4x+1=0を解いてみましょう。
x2+4x+1は因数分解できそうにありませんね。
x2+4x+1を平方完成すると(x+2)2-3となります。
※平方完成がわからない人は平方完成のやり方について解説した記事をご覧ください。
つまり(x+2)2-3=0より、(x+2)2=3となります。
x+2=±√3となるので、答えはx=-2±√3・・・(答)となります。
もしくは解の公式を使っても良いです。二次方程式x2+4x+1=0を解の公式を使って解くと、
x = -2±√22-1×1 = -2±√3・・・(答)となりますね。
※解の公式とは何かについて解説した記事もご用意しているので、ぜひ参考にしてください。
以上が二次方程式を因数分解できないときの解き方になります。
特に解の公式は大学入試や共通テストでも頻出なので、必ず覚えておきましょう。
平方完成と解の公式についてもっと詳しく学習したい人は二次方程式の解き方3パターンをご紹介した記事をご覧ください。
因数分解を利用した二次方程式の練習問題
最後に因数分解を利用した二次方程式の練習問題をご用意しました。
因数分解の練習としても非常に有効なので、ぜひ解いてみてください。
【練習問題】
以下の二次方程式を解きなさい。
(1)x2=4x
(2)x2+27=-12x
(3)3x2+7x+4=0
(4)6x2+17x+5=0
【解答&解説】
(1)x2-4x=0より、左辺をくくって、x(x-4)=0となるのでx=0、4・・・(答)となります。
(2)-12xを左辺に移行します。
x2+12x+27=0より、x2+12x+27を因数分解して(x+3)(x+9)となるのでx=-3、-9・・・(答)となります。
(3)3x2+7x+4を因数分解すると(3x+4)(x+1)となるのでx=-4/3、-1・・・(答)となります。
(4)6x2+17x+5を因数分解すると(2x+5)(3x+1)となるのでx=-5/2、-1/3・・・(答)となります。
今回は二次方程式を因数分解を使って解く方法をパターン別に解説していきました。
因数分解できないときは平方完成か解の公式を使って解くということを忘れないでください!


