中学数学で比例を習うと、比例のグラフを書いてみるというシーンが必ず登場します。
しかし、比例のグラフの書き方がよくわからないという中学生も多いのではないでしょうか?
そこで今回は早稲田大学教育学部数学科を卒業した筆者が比例のグラフの書き方についてステップごとに図解でわかりやすく解説します。
また、比例のグラフの特徴についても解説していくので、ぜひ最後までお読みください。
※比例とは何かについて解説した記事もぜひ合わせてご覧ください。
比例のグラフの書き方を例題でわかりやすく解説
今回はy=2xのグラフを書いていきましょう。
y=2xは
- x=1のときy=2
- x=2のときy=4
- x=3のときy=6
- x=4のときy=8
であり、xの値が2倍、3倍・・・となるにつれてyの値も2倍、3倍・・・となるので、確かに比例の式であることがわかります。
※ちなみですが、y=2xの2のことを比例定数というのでした。詳しくは比例定数とは何かについて解説した記事をご覧ください。
比例のグラフの書き方は以下のステップとなります。
- xy座標を書く
- y=2xが通る原点O以外の点を1つ書き出す
- 原点Oと2で書き出した点を直線で結ぶ
では、順番に解説していきます。
xy座標を書く
まずはxy座標を書きましょう。今回はわかりやすいようにあらかじめ目盛りとマス目が記載されたxy座標を使用します。
※xy座標がわからない人はxy座標とは何かについて解説した記事をご覧ください。
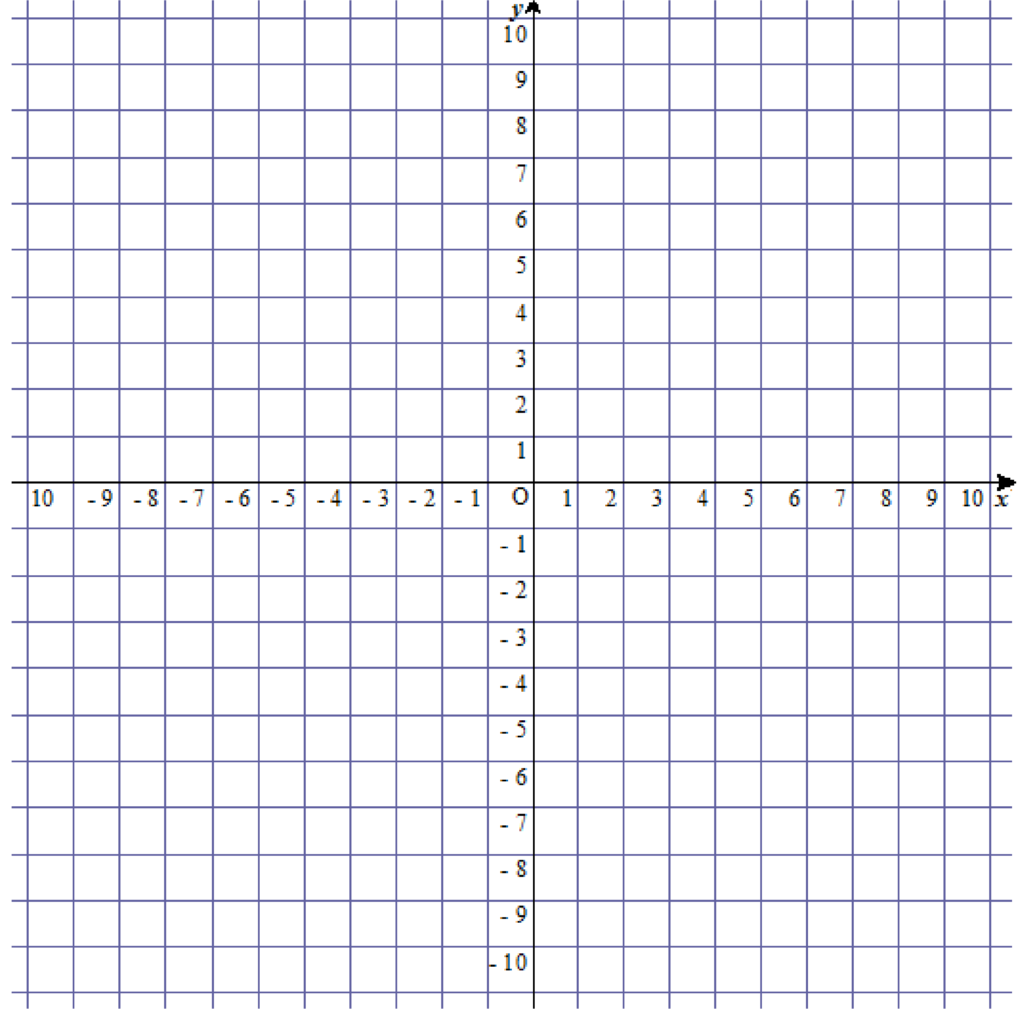
y=2xが通る原点O以外の点を1つ書き出す
y=axの式においてはaがどんな値であろうともx=0のとき必ずy=0です。
なので、y=axという比例の式は必ず原点O(0、0)を通ります。
あとは、この原点O以外にy=2xが通る点を1つ見つけましょう。
xに適当な数を入れれば問題ありません。今回はx=1を代入してみましょう。
x=1のとき、y=2ですね。つまり、y=2xは点(1、2)を通ることがわかります。
なので、先ほど書いたxy座標上に点(1、2)を書きましょう。
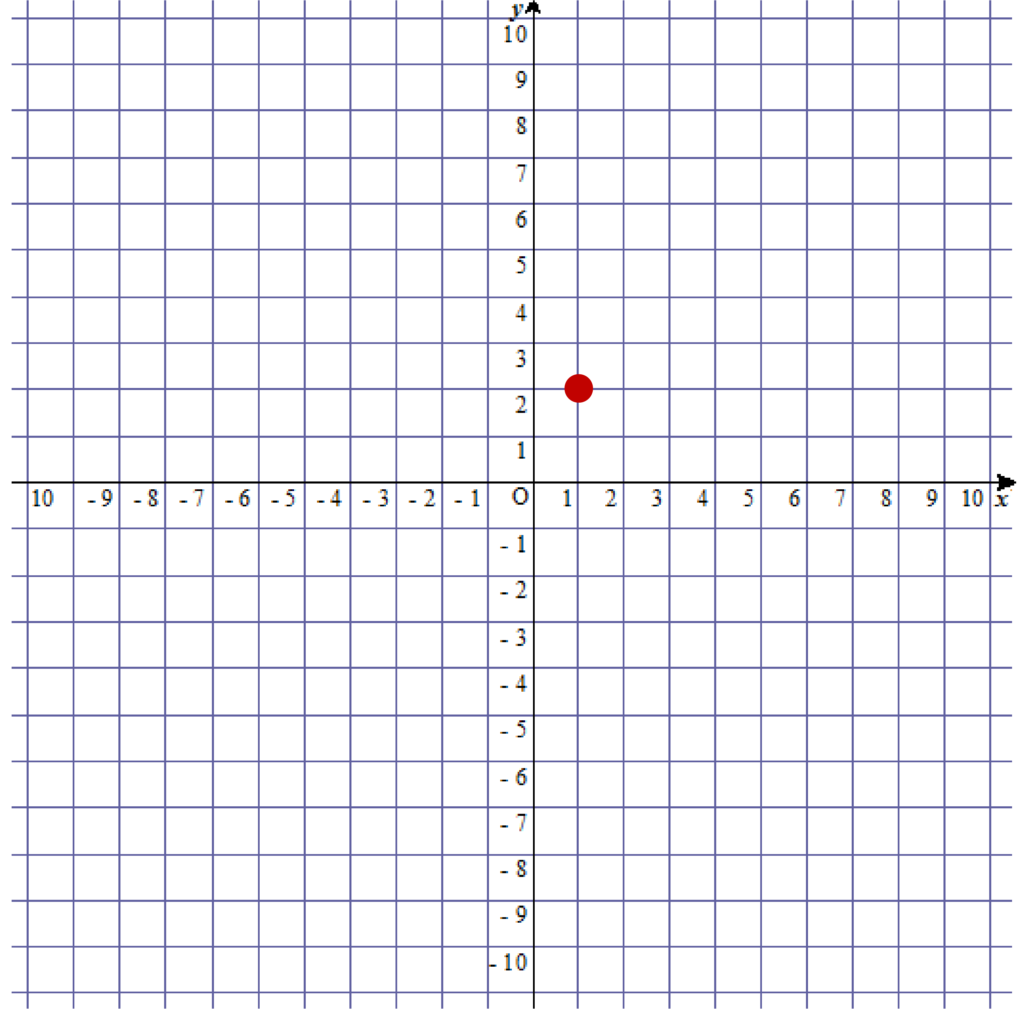
原点Oと2で書き出した点を直線で結ぶ
いよいよ最後のステップです。
あとは原点Oと先ほど書いた点(1、2)を以下のように直線で結ぶだけです。
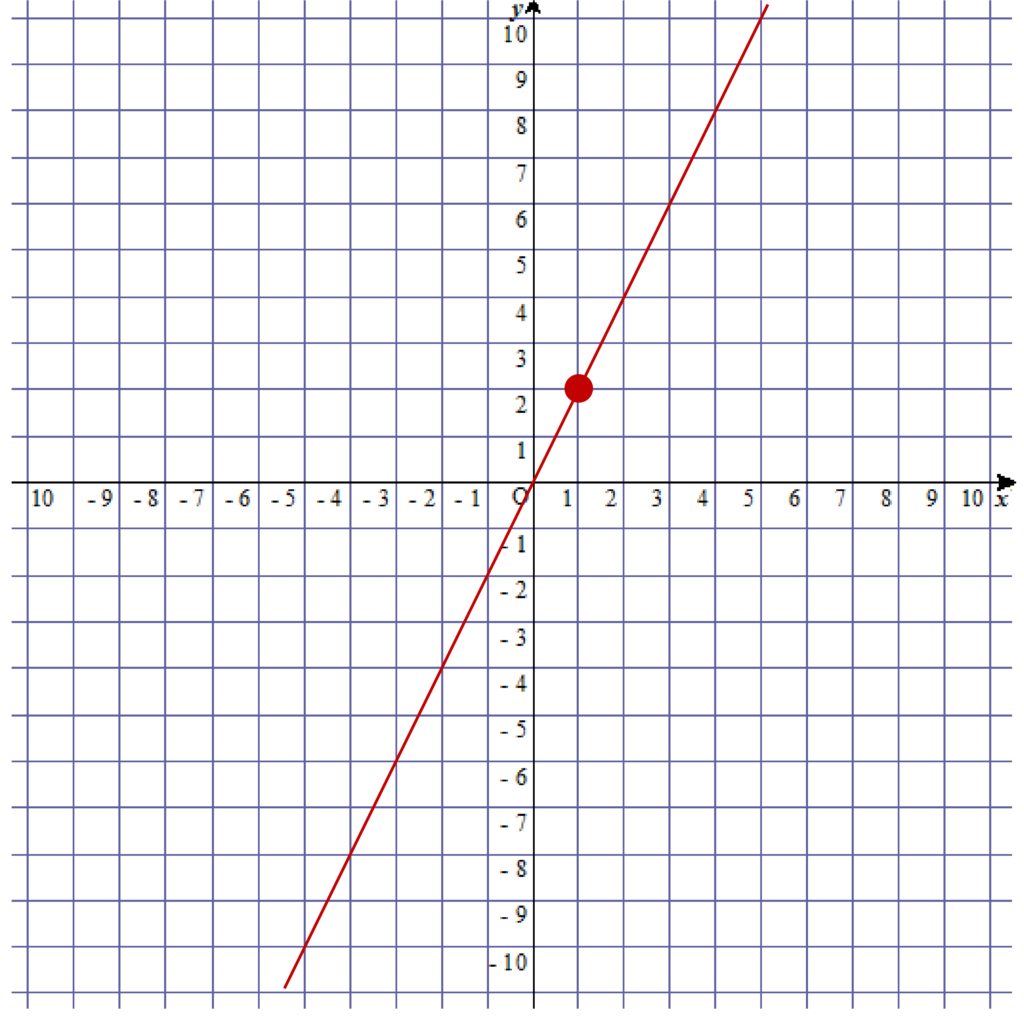
これでy=2xのグラフは完成です。
ちなみにですが、y=2xのグラフは(2、4)や(3、6)(4、8)(-1、-2)(-2、-4)(-3、-6)なども通るので、以上で書いた直線がしっかりと上記の点も通ることに注意しましょう。
比例のグラフの書き方その2
では、次はy=1/2xのグラフを書いてみましょう。
グラフの書き方は先ほどと変わりませんのでサクッと書いていきます。
まずはxy座標を書きます。

そして、y=1/2xはx=2のときy=1ですね。
なので、xy座標上に点(2、1)を書きましょう。
※例えばx=1のときy=1/2なので、点(1、1/2)をとっても良いのですが、マス目が振られている場合は1/2は取りづらいので、x、yともに整数になる点を考えた方がグラフは書きやすいです。
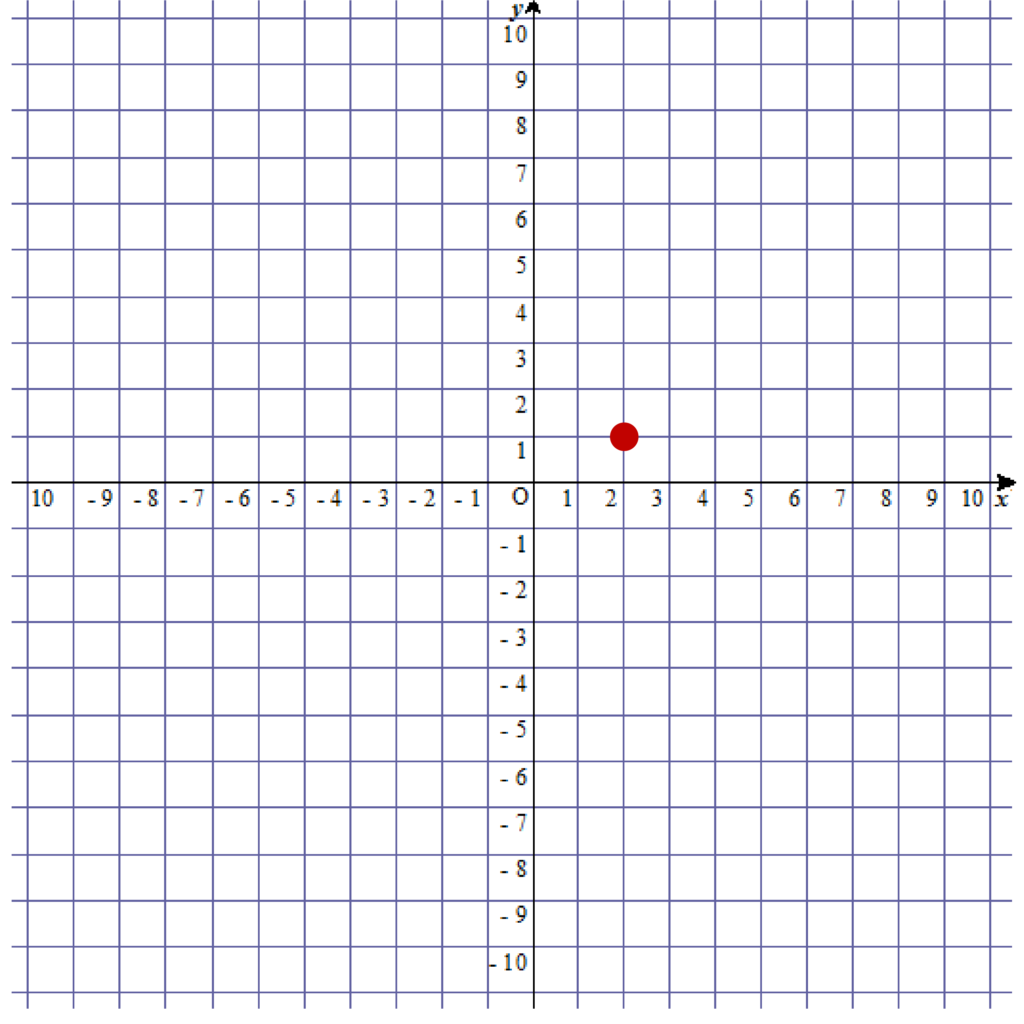
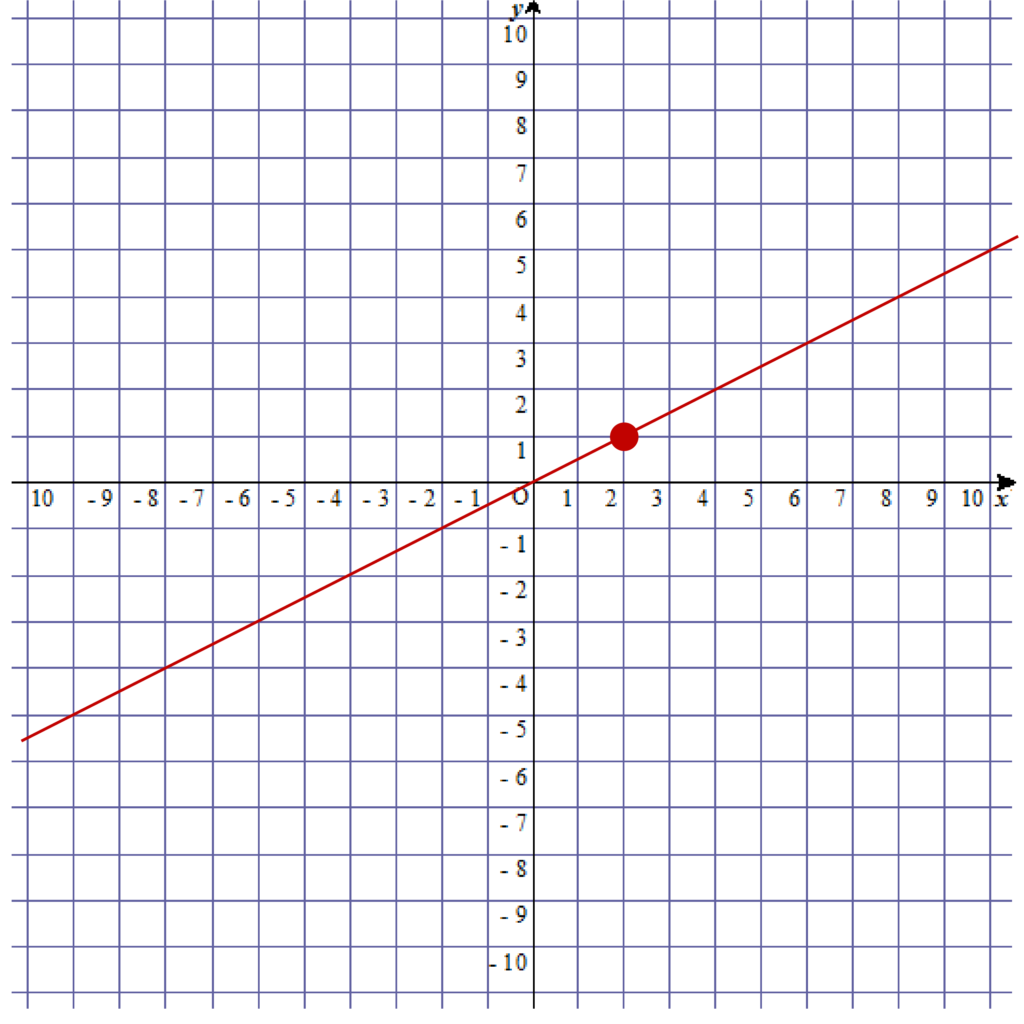
最後は原点Oと先ほど書いた点(2、1)を結んでグラフは完成です。
比例のグラフにおける特徴3つ
ここからは比例のグラフにおける特徴を3つご紹介していきます。
すべて重要なことなので、必ず頭に入れておきましょう。
比例のグラフは必ず直線になる
比例のグラフにおける特徴1つ目は、比例のグラフは必ず直線になるということです。途中で曲がったりはしません。
定規が手元にない状態で比例のグラフを書く場面があるかもしれませんが、その場合はなるべく直線になるように心がけながら比例のグラフを書きましょう。
比例のグラフは必ず原点Oを通る
比例のグラフ(y=ax)は必ず原点O(0、0)を通ります。
これは先ほども解説した通り、y=axにおいてはaがどんな値であろうともx=0のときy=0が成り立つからです(0に何をかけても0ですね)
なので、比例のグラフを書くときは、必ず原点Oを通るようにしなければなりません。
比例定数が大きいほどグラフの傾きは急になる
先ほどy=2xのグラフとy=1/2xのグラフを書きましたが、2つのグラフを見比べると以下のようになります。
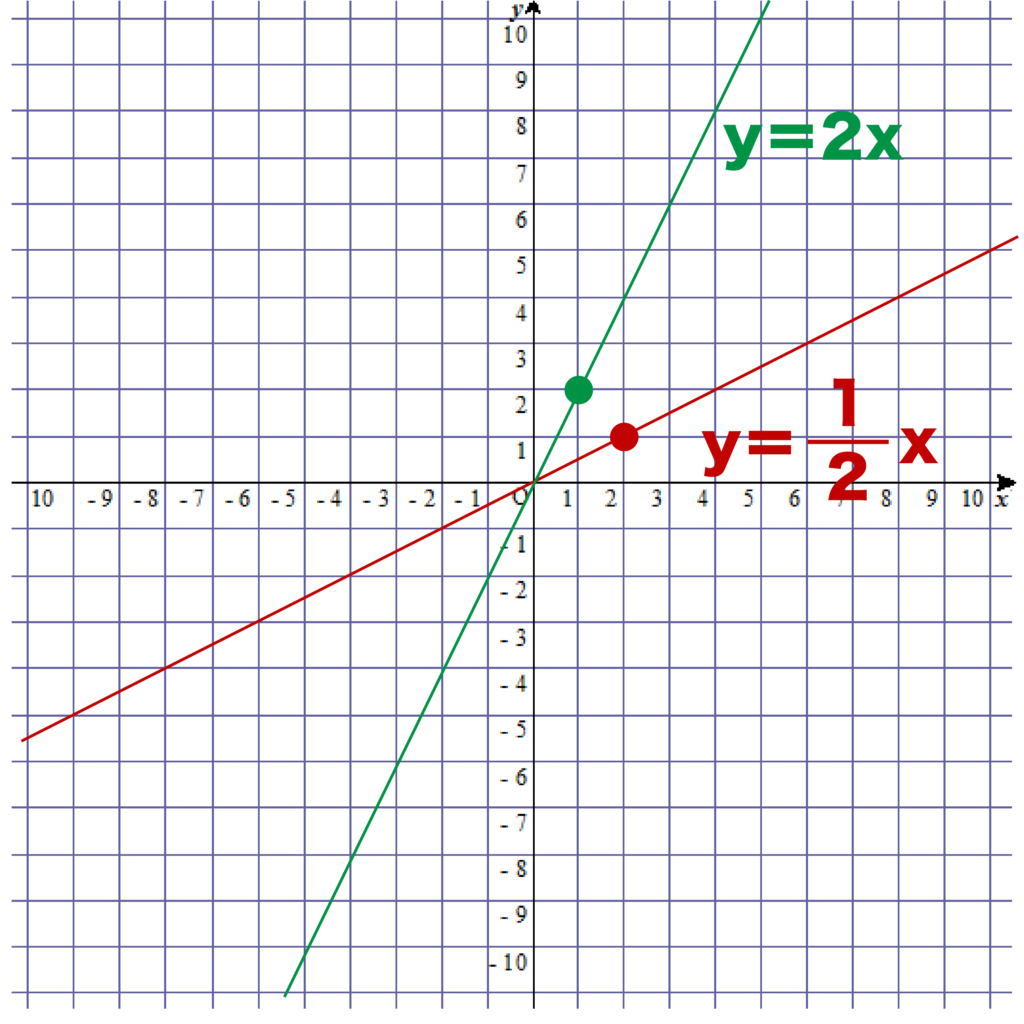
y=1/2xのグラフよりもy=2xのグラフの方が傾きが急になっていることがわかります。
比例の式y=axの比例定数aに注目してみると、aの値が大きければ大きいほどyの値は大きくなりやすいですね。
なので、一般的に比例の式y=axにおいては比例定数が大きいほどグラフの傾きは急になります。
※ちなみにですが、aのことを傾きと呼ぶ場合もありますので合わせて覚えておきましょう。
比例のグラフの書き方(目盛り・マス目がない場合)
最後に目盛り・マス目がない状態から比例のグラフを書く方法について解説します。
今回はy=3xのグラフを書いてみましょう。
書き方の手順は先ほど解説した3ステップと変わりませんのでご安心ください。
まずはxy座標を自分で書きましょう。この時点では目盛りもマス目も不要です。
x軸とy軸、原点Oの3つを忘れずに記載しましょう。
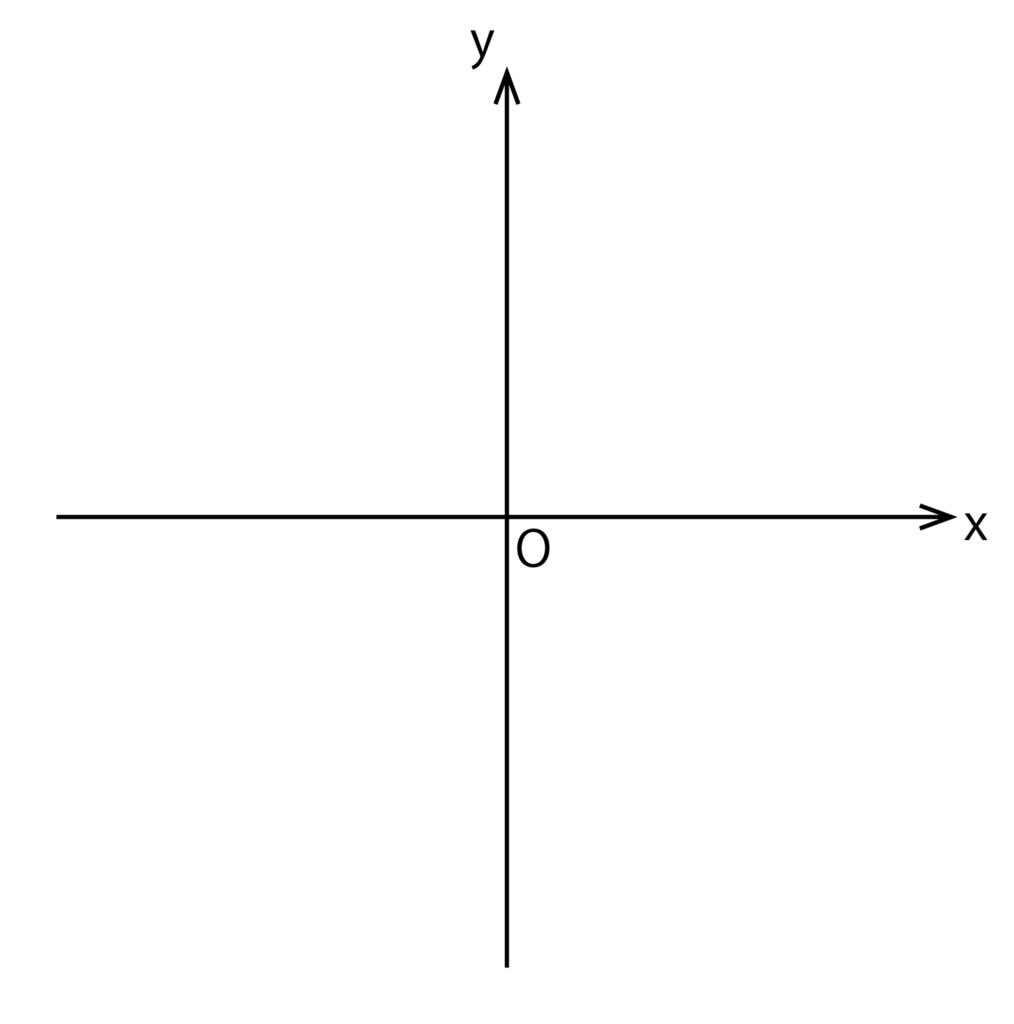
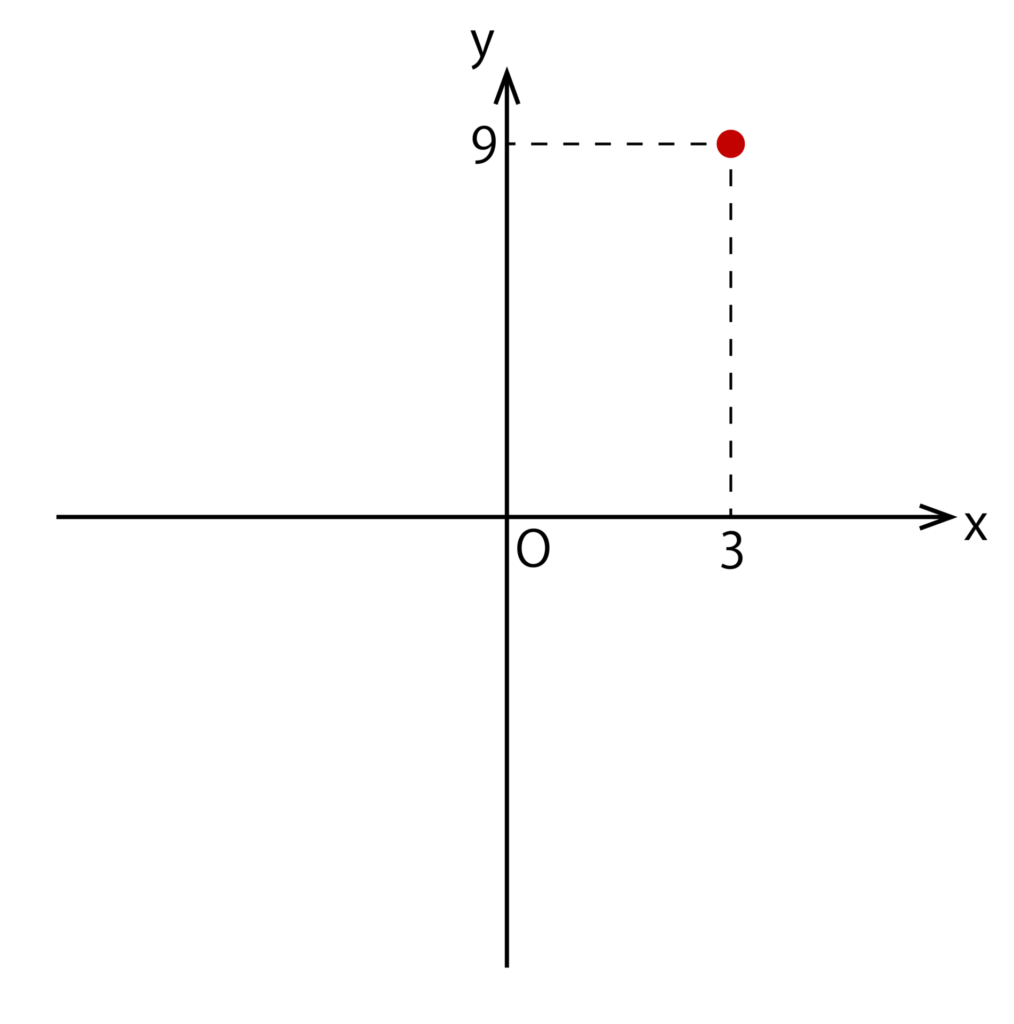
次にy=3xが通る原点O以外の点を1つ記載します。今回は以下のように点(3、9)を記載してみます。
x=3、y=9であることがわかるように3と9の目盛りは自分で記載する必要がありますが、マス目は記載する必要はありません。
最後は先ほど書いた点(3、9)と原点Oを直線で結びましょう。
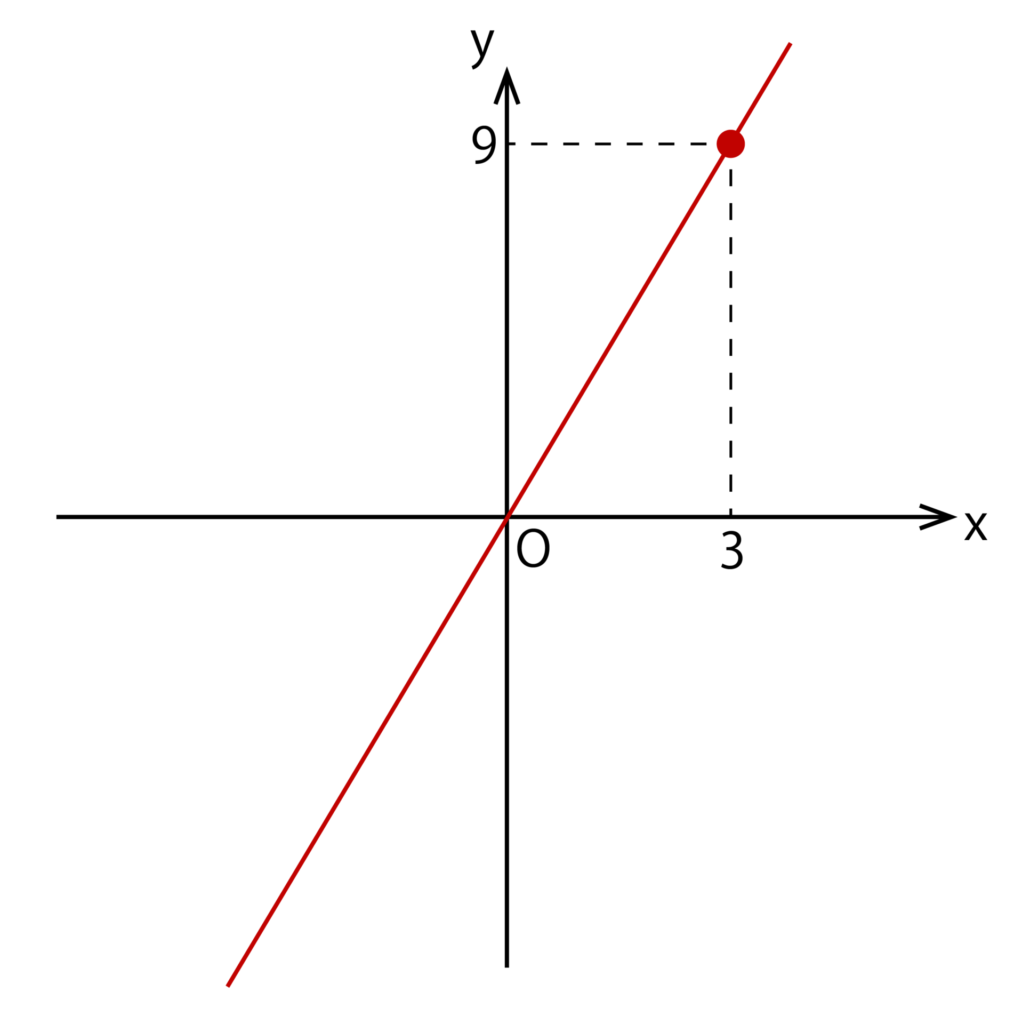
以上でy=3xのグラフが書けました。
いかがでしたか?今回は比例のグラフの書き方3ステップと比例のグラフの特徴について解説しました。
比例のグラフを書く機会はこの先もたくさん登場します。グラフの書き方を忘れてしまったときはぜひ本記事を見返してください。


