素因数分解はもともとは中学3年生で学習する内容でしたが、2021年の新学習指導要領から中学1年生で学習することになりました。
しかし、素因数分解は中学1年生でも理解できる内容なのでご安心ください。
素因数分解は今後、中学数学だけでなく高校数学でも登場するかなり重要な用語です。必ずできるようにしておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者が素因数分解とは何かについて解説した後、素因数分解のやり方やコツ・裏ワザなどをご紹介していきます。
また、素因数分解に関するよくある質問にも回答しているので、ぜひ最後までご覧ください。
素因数分解とは?中学生向けにわかりやすく解説
素因数分解とは自然数を素数だけの積(=掛け算)の形で表すことです。
※素数とは自然数(=1以上の整数)において1と自分自身の数しか約数を持たない数のことです。詳しくは素数とは何かについて解説した記事をご覧ください。
例えば、10という自然数は素数だけの掛け算の式2×5で表すことができますね。
つまり、10を素因数分解すると2×5になるということです。
36を素因数分解すると、22×32となります。2も3も確かに素数です。
以上が素因数分解とは何かについての解説となります。
素因数分解のやり方
ここからは素因数分解のやり方について解説します。
素因数分解のやり方は簡単です。素因数分解したい自然数を素数でどんどん割っていくだけです。
例えば、90を素因数分解する場合、以下のようにやっていきます。
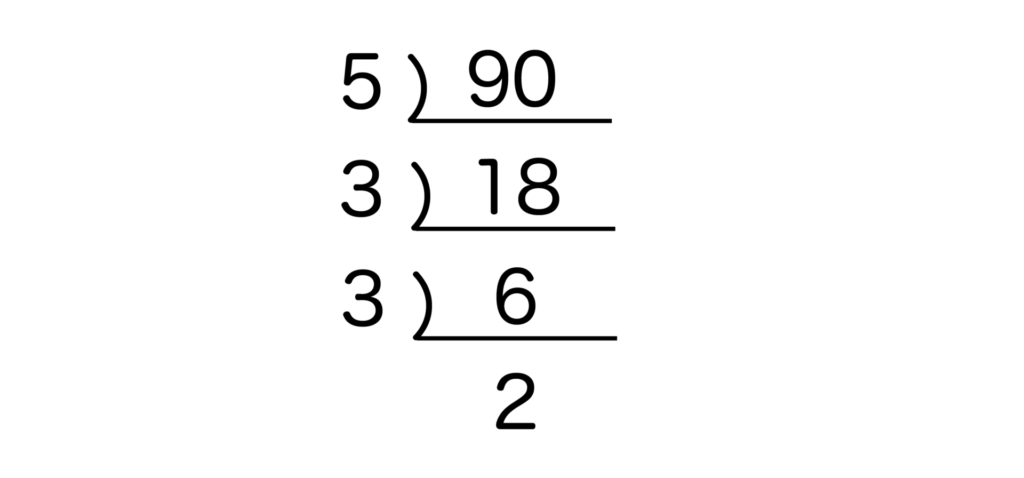
まず、90は素数である5で割れそうなので、90の横に5を書いて、90÷5を行います。
90÷5は18なので、90の下に18を書きます。そして、18は何の素数で割れるかをまた考えます。
すると、素数である3で割れそうなので、18÷3をして、その結果である6を18の下に書きます。
6は素数である3で割れるので、6÷3をして、その結果である2を6の下に書きます。
2は素数なので、これ以上素数で割ることはできなさそうです。
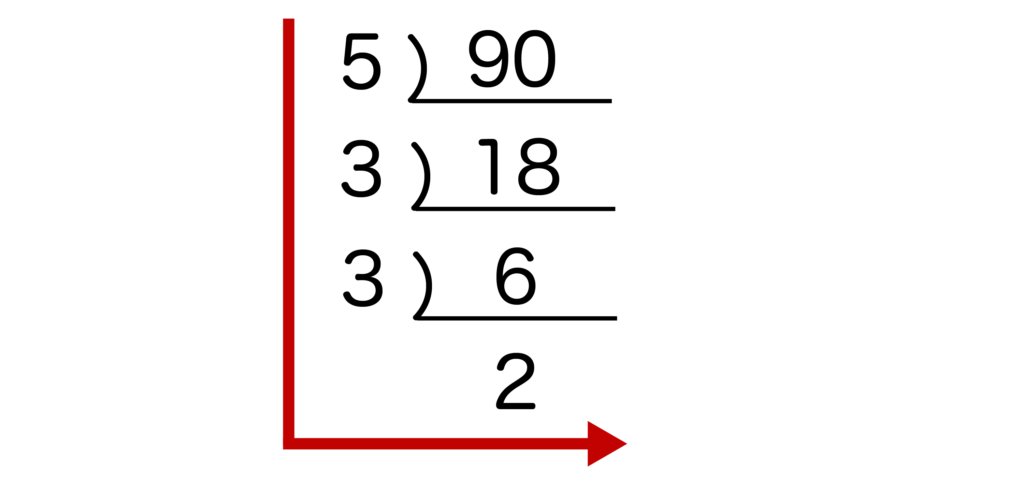
最後は、以下の赤線のように書いた数字を調べます。
5が1個、3が2個、2が1個ありますね。よって、90を素因数分解すると、2×32×5となります。
※2も3も5もすべて素数ですね。
2×32×5=2×9×5で確かに90になっていることが確認できます。
以上が素因数分解のやり方です。素因数分解したい自然数をどんどん素数で割っていくという非常にシンプルなやり方なので、必ずできるようにしておきましょう。
素因数分解に裏ワザ・コツはある?
では、素因数分解に裏ワザ・コツはあるのでしょうか?
残念ながら、先ほどご紹介した素因数分解のやり方が最もシンプルかつ簡単な方法となります。
しかし、あえて裏ワザ・コツをあげるとすれば、32=9、52=25など素数の2乗を数を意識して素因数分解を行うことです。
例えば、先ほどの90を素因数分解する場合、以下のようにいきなり9で割ってしまいます。
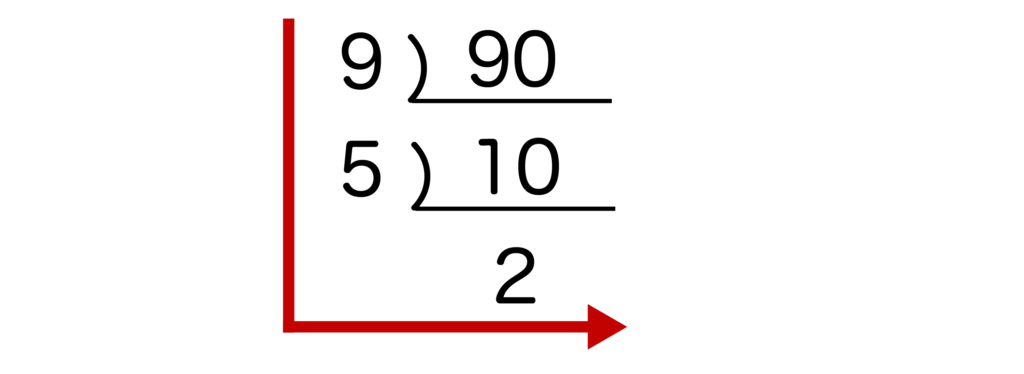
9=32が頭に入っていれば、以上から90=2×32×5を導くことができます。
割る回数が減るので、少しだけ素因数分解が楽になるケースもあるでしょう。ぜひ試してみてください。
素因数分解の計算機・サイトはある?
素因数分解に慣れて確実に自力で素因数分解できるようになれば、大きい数をいちいち素因数分解するのが面倒に感じるときもあるでしょう。
そんな人のために素因数分解の計算機・サイトを念のためご紹介しておきます。
例えば、459032を素因数分解の計算機(サイト)を使って素因数分解してみましょう。
まずは素因数分解計算機にアクセスします。
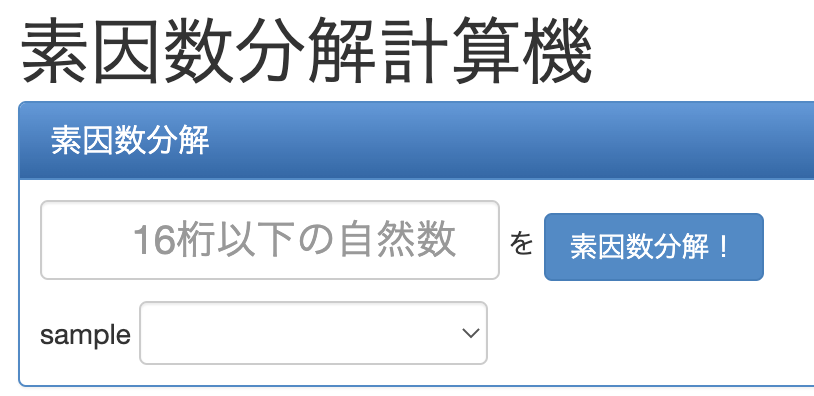
そして、上記の「16桁以下の自然数」と書かれた欄に今回 素因数分解したい459032を入力して「素因数分解!」ボタンをクリックします。
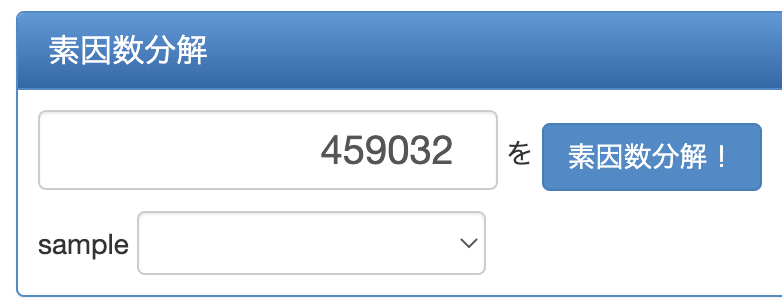
すると以下の画面のように、459032を素因数分解すると23×72×1171となることがわかりました。
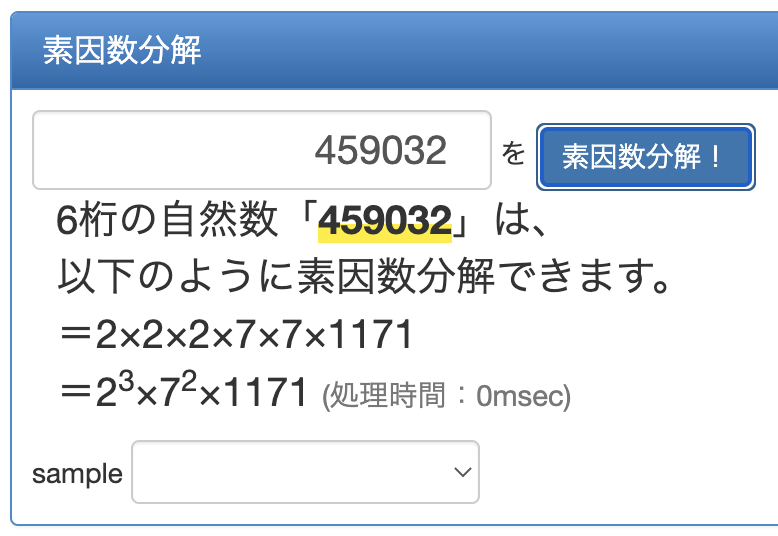
どんな数でも一瞬で素因数分解してくれるとても便利なサイトなので、ぜひ皆様も一度使ってみてください。
素因数分解の一意性とは?
中学数学・高校数学では学習しませんが、素因数分解の一意性という言葉があるので簡単にご紹介だけしておきます。
興味がある人はぜひご覧ください。
一意性とは「ただ一通りしかないこと」です。
つまり、素因数分解の一意性とはある自然数を素因数分解すると、その結果は一通りしかないことを意味しています。
先ほど、90を素因数分解すると2×32×5になることがわかりましたが、これ以外のパターンは1つもありません。90を素因数分解した結果は2×32×5のみです。
当たり前といえば当たり前のことなので、中学数学・高校数学において素因数分解の一意性を意識する必要性はありませんが、素因数分解の一意性を証明しようとすると実はかなり大変です。
本記事ではその証明は割愛しますが、素因数分解の一意性という言葉は知っておいて損はないでしょう。
素因数分解は何に使われる?
では、自然数を素因数分解することによってどんなことができるのでしょうか?
最も有名なのは、その自然数の約数の個数と約数の総和を求めることです。
例えば、先ほど90=2×32×5に素因数分解しましたが、
- 90の約数の個数=(1+1)×(2+1)×(1+1)=12[個]
- 90の約数の総和=(1+2)×(1+3+9)×(1+5)=234
となります。詳しくは約数の個数と総和の公式・求め方について解説した記事をぜひご覧ください。
素因数分解のよくある疑問
ここからは素因数分解のよくある疑問について回答していきます。
【質問1】ルートがついている数は素因数分解できますか?
【回答】できません。冒頭でも解説した通り、素因数分解できる数は自然数のみです。
【質問2】素因数分解はいつ習いますか?
【回答】中学1年生で習います。もともとは中学3年生で習う内容でしたが、2021年の新学習指導要領から中学1年生で習う内容に移行されました。
【質問3】337は素因数分解できますか?
【回答】できません。337は素数です。
素因数分解の練習問題
最後に素因数分解の練習問題をご用意しました。
素因数分解に慣れる練習として取り組んでみましょう。
【問題】
以下の自然数を素因数分解しなさい。
(1)91
(2)42
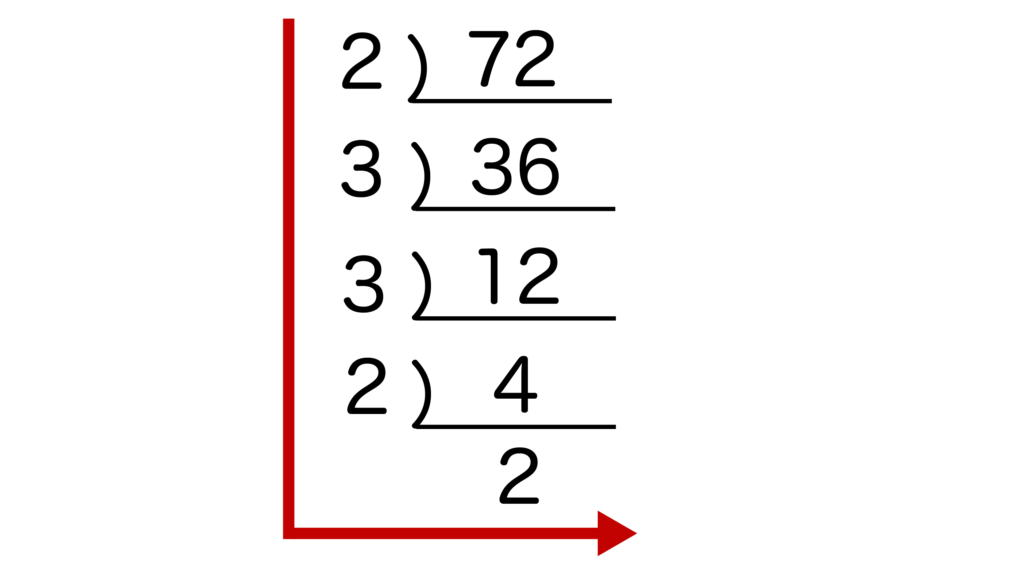
(3)72
(4)54
(5)576
(6)289
【解答&解説】
(1)91を素因数分解すると、7×13になります。
(2)42を素因数分解すると、2×3×7になります。
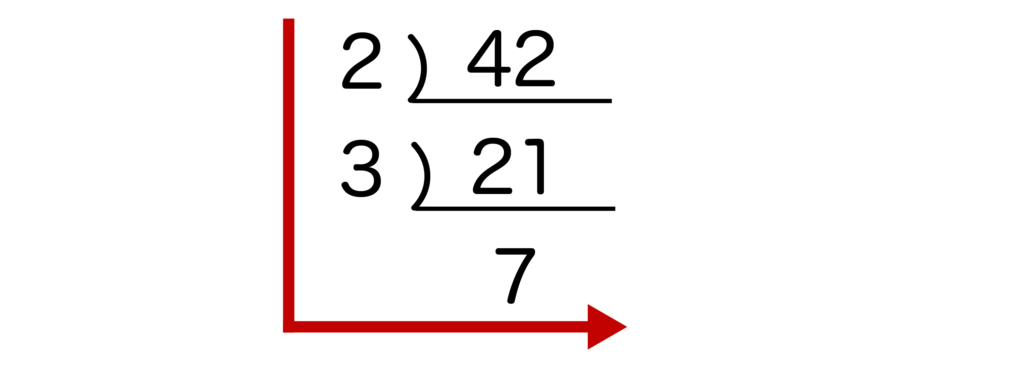
(3)72を素因数分解すると、23×32になります。
(4)54を素因数分解すると、2×33になります。
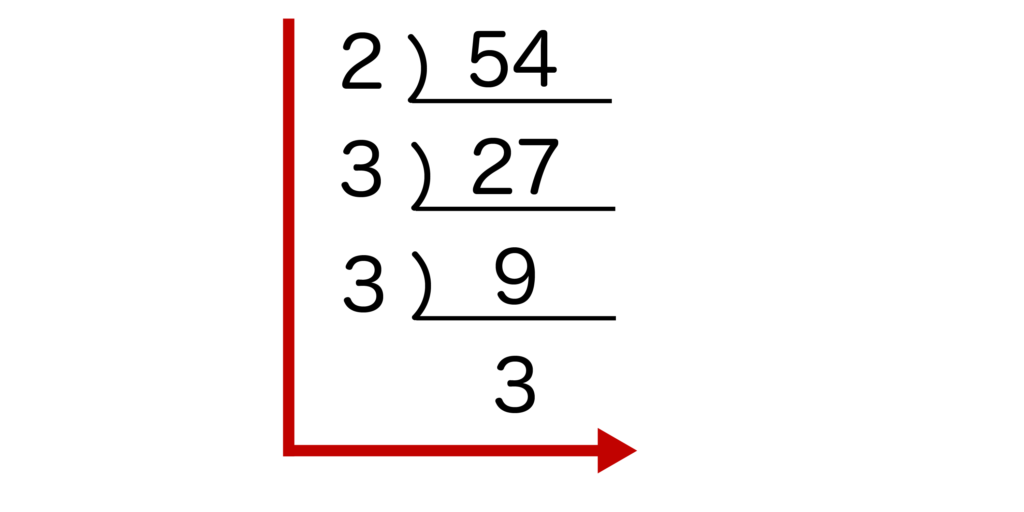
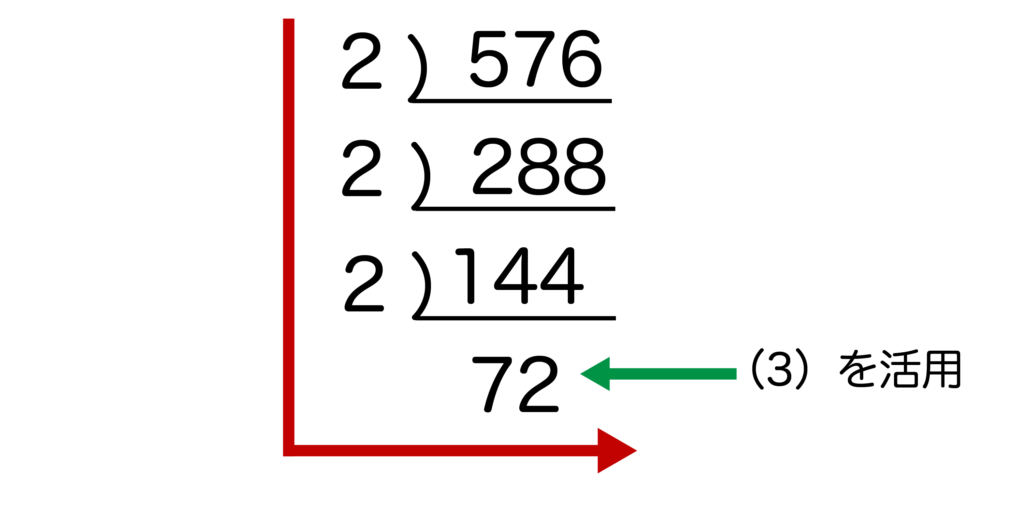
(5)576を素因数分解すると、26×32になります。
以下のように576を素数で割っていくと72が出現します。(3)より72を素因数分解すると23×32になることがわかっているので、合計で2が6個、3が2個あることがわかります。
(6)289を素因数分解すると、172になります。
いかがでしたか?
今回は素因数分解とは何かについて解説した後、素因数分解とはのやり方や裏ワザ・コツ、素因数分解をすることでできることなどをご紹介していきました。
素因数分解はこれから数学の問題を解いていくにあたって必須のテクニックです。たくさんの問題を解いて素因数分解に今のうちに慣れておきましょう。


