中学数学では後ほど詳しく解説しますが、負の数という概念が登場します(小学校まででは正の数のみを取り扱っていました)
負の数はこの先の高校数学でもずっと使い続けるので、ここでつまずいてしまうとこの先の数学の学習に苦労してしまいます。なので、必ず理解しておきましょう。
本記事では早稲田大学教育学部数学科を卒業した筆者が正の数・負の数とは何かについてや計算の仕方などについてわかりやすく解説していきます。
また、0は正の数かどうかなどのよくある疑問にも回答しています。
最後には正の数・負の数の計算問題も用意しているので、ぜひ最後までご覧ください。
正の数・負の数とは?わかりやすく解説
正の数は「せいのすう」と読み、0よりも大きい数のことを指します。正の数には正の符号「+(プラス)」をつけて表すことがあります。
例としては+6、+10、+9.4、+2/3などがあります。
正の数において正の符号「+」は記載しなくても問題はありません。
負の数は「ふのすう」と読み、0よりも小さい数のことを指します。負の数には負の符号「-(マイナス)」をつけて表します。
正の数の符号「+」と違って、負の数を表現するには「-」は必ずつけなければなりません。
例としては-5、-10、-5.6、-3/10などがあります。
0は正の数?負の数?
0は正の数でも負の数でもありません。
なので、0には「+」「-」もどちらもつけることはありません。
ちなみにですが、0は整数の一種であり、整数は正の整数・負の整数・0の3つに分類されます。
正の整数の例としては1、10、50、105などがあげられます。
負の整数の例としては-1、-3、-10、-99などがあげられます。
正の整数は自然数とも呼ばれているので、合わせて覚えておきましょう。
正の数・負の数を数直線で表現してみよう
数直線は小学校でも学習したかと思いますが、中学数学・高校数学でも引き続き登場します。
負の数は数直線において、0よりも左の方に伸ばした直線上で表現することができます。
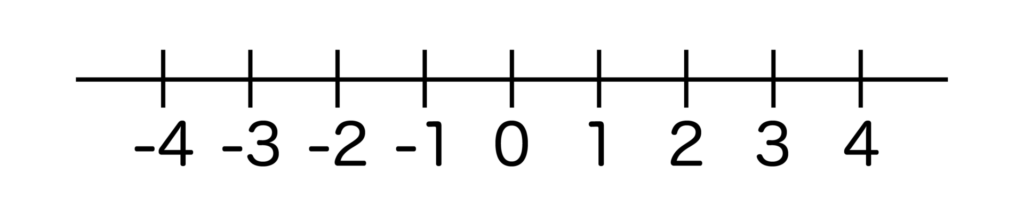
数直線において0の位置を原点というので覚えておきましょう。
また、数直線においては右の方向に行くほど数は大きくなり、左の方向に行くほど数は小さくなります。
右の方向のことを正の方向といい、左の方向のことを負の方向といいます。
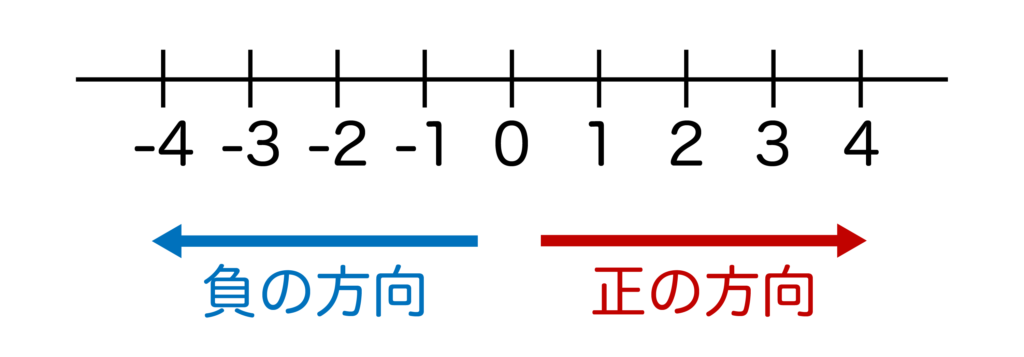
正の数・負の数の絶対値
数直線上において、原点(=0)からの距離のことを絶対値といいます。
距離なので、絶対値は必ず正の数になります。
例えば、以下の数直線を使って4と-3の絶対値を考えてみます。
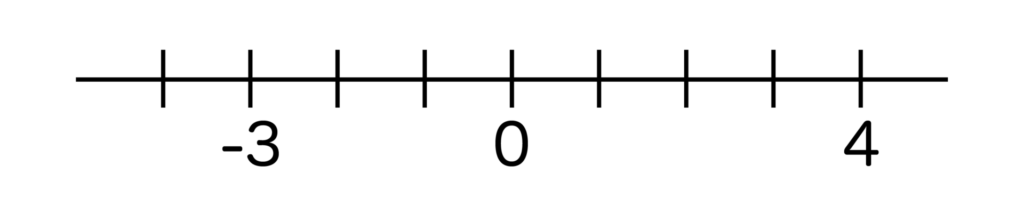
まず4の絶対値からですが、4は原点からの距離=4ですね。よって4の絶対値=4となります。
次に-3の絶対値ですが、-3は上記の数直線において原点からの距離=3ですね。よって-3の絶対値=3となります。
絶対値は原点からの距離を表すので「+」や「-」の符号を付けてはいけません。
ちなみにですが、0の絶対値は0となります。
正の数・負の数の計算の仕方
ここからは正の数・負の数の計算の仕方について解説します。
計算には足し算・引き算・掛け算・割り算の4つがあるので、それらについて順番に解説していきます。
足し算
正の数+正の数の計算の仕方は小学校で習っているので割愛します。
まずは正の数+負の数の計算の仕方から解説します。
例えば、10+(-4)を計算してみます。
正の数・負の数の計算における足し算・引き算では+と-が並んだら-に変わるということを覚えておきましょう。
10+(-4)では、+と-が並んでいますね。なので、10+(-4)=10-4となります。
10-4=6なので、10+(-4)=6となります。
では、負の数+負の数の計算はどうでしょうか?
-4+(-9)を計算してみます。
先ほど解説した通り、+と-が並んだら-に変わるので、-4+(-9)=-4-9と書き換えることができます。
-4-9は、数直線でいうと-4の位置からさらに左方向(負の方向)に9だけ進むことを示しているので、-4-9=-13となります。
つまり、-4+(-9)=-13となるのです。
引き算
正の数-正の数の計算の仕方は小学校で習っているので割愛します。
正の数-負の数を考えてみましょう。
例として5-(-4)を計算してみます。
正の数・負の数の計算における足し算・引き算では-と-が並んだら+に変わります。
つまり、5-(-4)=5+4になるのです。5+4=9なので、5-(-4)=9となります。
では、負の数-負の数はどうなるでしょうか?
ちなみにですが、中学数学からは足し算のことを加法、引き算のことを減法といいます。加法・減法について詳しく解説した記事もご用意しているので、ぜひ参考にしてください。
掛け算
正の数・負の数の計算における掛け算では、
- 正の数×負の数=負の数
- 負の数×負の数=正の数
になります。
例として5×(-8)を計算してみます。
5は正の数で-8は負の数なので、答えは負の数になります。5と8をかけると40ですね。
よって答えは-40となります。
では、-10×(-4)はどうなるでしょうか?
-10は負の数で、-4も負の数なので答えは正の数となります。10と4をかけると40なので、答えは40となります。
ちなみにですが、掛け算のことは乗法と言います。乗法とは何かについて解説した記事もぜひ参考にしてください。
割り算
正の数・負の数の計算における割り算では、掛け算のときと同様に
- 正の数÷負の数=負の数
- 負の数÷負の数=正の数
になります(負の数÷正の数も負の数となります)
例として70÷(-2)を計算してみましょう。
70は正の数で-2は負の数なので答えは負の数となります。
70÷2=35なので、答えは-35となります。
次は-40÷(-8)を計算してみましょう。
-40も-8も負の数なので、答えは正の数になります。
40÷8=5なので、答えは5となります。
ちなみにですが、割り算のことは除法と言います。除法とは何かについて解説した記事もぜひ参考にしてください。
以上が正の数・負の数の計算の仕方となります。
特に掛け算と割り算において計算結果の符号が何になるか?は非常に重要なので、上記でご紹介した事柄は必ず頭に入れておきましょう。
正の数・負の数の計算問題
最後に正の数・負の数の計算問題を用意しました。正の数・負の数に慣れるにはたくさんの計算問題を解くことが重要です。ぜひ解いてみてください。
【問題】
以下の計算を行いなさい。
(1)4+(-2)
(2)-5+10
(3)-8-3
(4)-17+(-12)
(5)16-(-3)
(6)100-(-92)
(7)-15-40
(8)4×(-3)
(9)-11×2
(10)-45×(-5)
(11)45÷(-9)
(12)-60÷3
(13)-85÷(-5)
【解答&解説】
(1)4+(-2)=4-2=2
(2)-5+10=5
(3)-8-3=-11
(4)-17+(-12)=-17-12=-29
(5)16-(-3)=16+3=19
(6)100-(-92)=100+92=192
(7)-15-40=-55
(8)4×(-3)=-12
(9)-11×2=-22
(10)-45×(-5)=225
(11)45÷(-9)=-5
(12)-60÷3=-20
(13)-85÷(-5)=17
いかがでしたか?今回は正の数・負の数とは何か?や正の数・負の数の絶対値・計算の仕方などについて解説していきました。
正の数・負の数は中学数学の入門となる分野です。ここでつまずいてしまうとこの先の数学の学習がスムーズにいかなくなってしまうので、必ずできるようにしておきましょう!


