多項式の計算は高校数学の基礎となっており、必ずマスターしておかなければなりません。
しかし、多項式の計算においては多くの公式があり、頭の中が混乱してしまっている高校生もいるのではないでしょうか?
そこで本記事では、早稲田大学教育学部数学科を卒業した筆者が多項式の計算における基本公式や展開方法・解き方などを一挙にわかりやすく解説していきます。
多項式の計算における公式(基本)
数学1における多項式の計算では多くの公式が登場しますが、1つ1つは中身をしっかりと理解すれば全然難しくはありませんのでご安心ください。
※多項式とは何かをまだ理解できていない人は、多項式の定義について解説した記事をご覧ください。
まずは以下2つの公式(交換法則と結合法則)を理解しましょう。
| 加法 | 乗法 | |
|---|---|---|
| 交換法則 | A+B=B+A | AB=BA |
| 結合法則 | (A+B)+C=A+(B+C) | (AB)C=A(BC) |
加法とは足し算のこと、乗法とは掛け算のことです。
交換法則・結合法則ともに、足し算・掛け算ならどの順番で足しても掛けても結果は同じという法則です。
かなり当たり前のことなので、交換法則・結合法則は特に意識することはないでしょう。
そして、もう1つの法則として分配法則があります。
分配法則はA(B+C)=AB+AC、(A+B)(C+D)=AC+AD+BC+BDが成り立つことを言います。
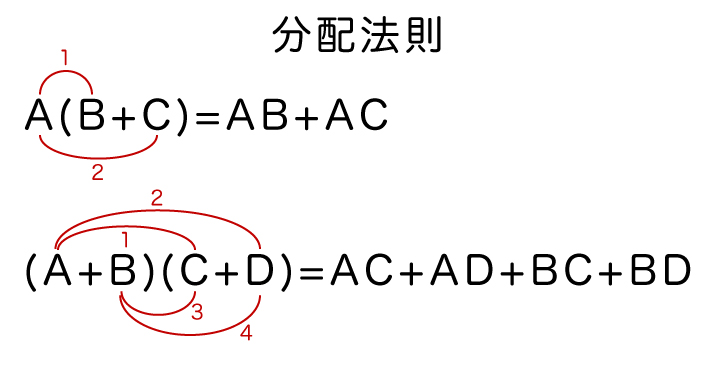
分配法則も中学で学習した内容なので、そこまで意識する必要はないかと思います。
まずは基本公式として上記3つ(交換法則・結合法則・分配法則)を理解しておきましょう。
多項式の加法・減法
先ほども解説した通り、加法は足し算のことです。それに対して減法は引き算のことです。
多項式の加法・減法は結局は同類項の整理という作業になります。
例えば、A=5x3+6x2+3x+8、B=9x3+3x2+5x+18において、
A+B=(5+9)x3+(6+3)x2+(3+5)x+(8+18)=14x3+9x2+8x+26となります。
次数が同じ項は係数の加法を行うことができます。
減法も同じです。A-B=(5-9)x3+(6-3)x2+(3-5)x+(8-18)=-4x3+3x2-2x-10となります。
多項式の指数法則
続いては多項式の指数法則について理解しましょう。
指数法則とは簡単に言うと、累乗に関する計算法則のことです。
以下3つの法則があります(m、nは正の整数とする)これは必ず覚えておきましょう。
- aman = am+n
- (am)n = amn
- (ab)n = anbn
これだけだとわかりにくいと思うので、具体例をあげていきます。
まずは1の具体例ですが、a2a7 = a2+7 = a9となります。
実際に数字を用いて検算してみます。指数法則に則ると、32×33=35=243となります。
32=9、33=27なので、9×27で確かに243になっていることがわかります。
2の具体例ですが、(a5)3 = a5×3 = a15 となります。
これも具体的な数字で検算してみましょう。例えば、(22)3を考えてみます。
指数法則をそのまま使うと、(22)3=26=64となります。
22=4なので、(22)3=43となり、確かに64になっています。
最後の3の具体例ですが、(ab2)=a2b2になるということです。
具体的な数字で検算しましょう。指数法則を使うと、(3×4)2 = 32 × 42 = 9×16=144となります。
3×4=12なので、122は確かに144になっています。
多項式の乗法
乗法は先ほども解説した通り、掛け算のことです。
単項式×単項式では、係数部分と文字部分の積をそれぞれ計算します。
例えば、3a2×8a5 = 3×8a2+5 = 24a7となります。
単項式×多項式では、分配法則を活用します。
例えば、3a2(5a3+6b)
=3a2 × 5a3 + 3a2 × 6b=15a5+18a2bとなります。
多項式×多項式も分配法則を活用します。
例えば、(2a6+3b2)×(7a6+2b7)
= 2a6 × 7a6 + 2a6 × 2b7 + 3b2 × 7a6 + 3b2 × 2b7
= 14a12 + 4a6b7 + 21a6b2 + 6b9となります。
ちなみにですが、乗法の反対(=割り算)は除法と言います。多項式の除法は数学1ではなく数学2で学習する内容となっていますので本記事では割愛させていただきます。
2次式・3次式の展開の公式
いよいよ最後の公式となります。以下で紹介する2次式の展開の公式は中学でも学習した内容ですが、念のため掲載します。
3次式の展開の公式は数学1ではなく数学2で学習する内容ですが、現段階で覚えておいて損はないのでご紹介します。
2次式の展開の公式
2次式の展開の公式は以下の5つです。
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2
(a+b)(a-b)=a2-b2
(x+a)(x+b)=x2+(a+b)x+ab
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
展開の公式は覚えることも重要ですが、練習問題をたくさん解いていくうちに自然と覚えるので、とにかく練習問題をたくさん解くことを意識しましょう。
3次式の展開の公式
3次式の展開の公式は以下の4つです。
(a+b)(a2-ab+b2)=a3+b3
(a-b)(a2+ab+b2)=a3-b3
(a+b)3=a3+3a2b+3ab2+b3
(a-b)3=a3-3a2b+3ab2-b3
3次式の展開の公式は2次式の展開の公式よりも少し覚えにくいですが、これも練習問題をたくさん解くうちに自然と覚えるので、そこまで気にしなくても大丈夫です。
多項式の計算(練習問題)
以上で数学1における多項式の計算に必要な公式はすべて揃いました。
ここからはひたすら練習問題を解いて慣れていくのみです。
練習問題1
A=x2+3y2-5xy、B=4x2+9、C=3x2+xy-4y2であるとき、以下の計算をせよ。
(1)A+B
(2)-3A+2B-C
(3)2(A+3C)-4(A-2B)
【解答&解説】
(1)A+B=(1+4)x2+3y2-5xy+9=5x2+3y2-5xy+9・・・(答)
(2)-3A+2B-C
=-3(x2+3y2-5xy)+2(4x2+9)-(3x2+xy-4y2)
=-3x2-9y2+15xy+8x2+18-3x2-xy+4y2
=2x2-5y2+14xy+18・・・(答)
(3)2(A+3C)-4(A-2B)=2A+6C-4A+8B=-2A+8B+6Cより、
-2(x2+3y2-5xy)+8(4x2+9)+6(3x2+xy-4y2)
=-2x2-6y2+10xy+32x2+72+18x2+6xy-24y2
=48x2-30y2+16xy+72・・・(答)
練習問題2
次の計算をせよ。
(1)(-xy3)2(-4x2y)
(2)3abc(a+b+c)
(3)(-xy)3(4x2+2y+8)
【解答&解説】
指数法則を使った練習問題となります。
(1)(-xy3)2=(-1)2x2y6より、x2y6 × (-4x2y)=-4x4y7・・・(答)
(2)分配法則を使います。
3abc(a+b+c)=3a2bc+3ab2c+3abc2・・・(答)
(3)(-xy)3(4x2+2y+8)
=(-1)3x3y3(4x2+2y+8)
=-x3y3(4x2+2y+8)
=-4x5y3-2x3y4-8x3y3・・・(答)
練習問題3
以下の式を展開せよ。
(1)(3x+2)(4x2+6x-5)
(2)(3x2+5x+2)(1-x-3x2)
(3)(a+5)2
(4)(3x-4y)2
(5)(4x+7y)(5x-9y)
(6)(a+3)3
(7)(2x-y)3
【解答&解説】
(1)分配法則を使います。
(3x+2)(4x2+6x-5)
=12x3+18x2-15x+8x2+12x-10
=12x3+26x2-3x-10・・・(答)
(2)こちらも分配法則を使います。
(3x2+5x+2)(1-x-3x2)
=3x2-3x3-9x4+5x-5x2-15x3+2-2x-6x2
=-8x2-18x3-9x4+3x+2
降べきの順に整理して、-9x4-18x3-8x2+3x+2・・・(答)となります。
※降べきの順がわからない人は、降べきの順・昇べきの順について解説した記事をご覧ください。
(3)(a+5)2
=a2+2×a×5+52
=a2+10a+25・・・(答)
(4)(3x-4y)2
=9x2-2×3x ×(-4y)+16y2
=9x2-24xy+16y2・・・(答)
(5)(4x+7y)(5x-9y)
=20x2-36xy+35xy-63y2
=20x2-xy-63y2・・・(答)
(6)(a+3)3
=a3+3×a2×3+3×a×32+33
=a3+9a2+27a+27・・・(答)
(7)(2a-b)3
=(2a)3-3×(2a)2×b+3×(2a)×b2-b3
=8a3-12a2b+6ab2-b3・・・(答)
練習問題4(応用問題)
最後に「おきかえ」を利用した応用問題をご紹介します。
大学入試や共有テストでも頻出のテクニックなので、解答&解説を読んでぜひ参考にしてください。
【問題】以下の式を展開せよ。
(1)(2a+b+c)2
(2)(a2+3a-2)(a2+3a+3)
【解答&解説】
(1)(2a+b+c)(2a+b+c)と考えて分配法則を使っても良いのですが、今回は2a+b=Aとおいてみます。
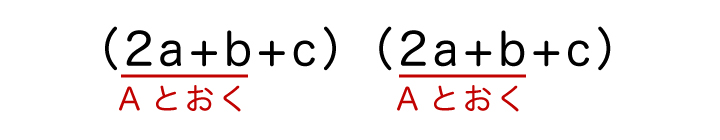
すると、(2a+b+c)2
=(A+c)2
=A2+2Ac+c2 となりますね。ここで、Aを2a+bに戻します。
すると、
(2a+b)2+2(2a+b)c+c2
=4a2+4ab+b2+4ac+2bc+c2・・・(答)と求めることができます。
(2)a2+3aが共通して存在しているので、これをAとおいてみましょう。
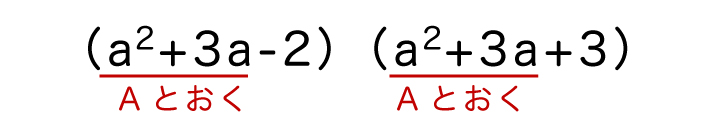
すると、(a2+3a-2)(a2+3a+3)
=(A-2)(A+3)
=A2+A-6 となりますね。ここで、Aをa2+3aに戻します。すると、
(a2+3a)2+(a2+3a)-6
=a4+6a3+9a2+a2+3a-6
=a4+6a3+10x2+3a-6・・・(答)となります。
いかがでしたか?
今回は多項式の計算に必要な公式や展開方法などを一挙に解説していきました。
本記事でご紹介したことは高校数学の基礎となっており、これが理解できていないとこの先の高校数学は確実につまずいてしまいます。ぜひ何回も見返して、基礎をマスターしてください。


