「内角の和が1800度である多角形は何角形か求めよ」と言われたら皆様は自力で求めることができますか?
数学の図形問題をこれから解いていくためには、1800°以外の値が登場してもスムーズに求められるようにしておかなければなりません。
本記事では早稲田大学教育学部数学科を卒業した筆者が内角の和が1800度の多角形を5秒で求める方法についてわかりやすく解説していきます。
全然難しい内容ではないので、数学や図形が苦手な人もぜひご覧ください。
内角の和が1800°の多角形5秒で求める方法
内角の和が1800°の多角形5秒で求める方法は内角の和の公式を使うことです。
内角の和の公式とは以下のことです。
「n角形の内角の和は(n-2)×180°求められる」
※なぜ上記の公式が成り立つのかについては内角・外角とは何かについて解説した記事をご覧ください。
内角の和が1800°ということは、(n-2)×180=1800が成り立つということですね。
すると、n-2=10より、n=12が求まります。
したがって、内角の和が1800°の多角形は十二角形であることがわかりました。
以上の内角の和の公式を知っていれば、内角の和が1800°の多角形は何角形かを5秒で求めることができます。
非常に便利な公式なので、必ず覚えておきましょう。
ちなみにですが、正多角形の場合、1つの内角の大きさはどれも同じになります。
よって、正十二角形の1つの内角の大きさ=1800°÷12=150°となります。
また、内角と同様に正多角形の1つの外角の大きさはどれも同じであり、外角=180°-内角で求められるので、正十二角形の1つの外角の大きさ=180°-150°=30°となります。
十二角形の内角の和は本当に1800°か確認してみよう
念のため、十二角形の内角の和は本当に1800°か確認してみましょう。
まずは以下のように十二角形を書いてみます。
そして、以下のように1つの頂点から対角線を引いて十二角形の中に三角形を作りましょう。
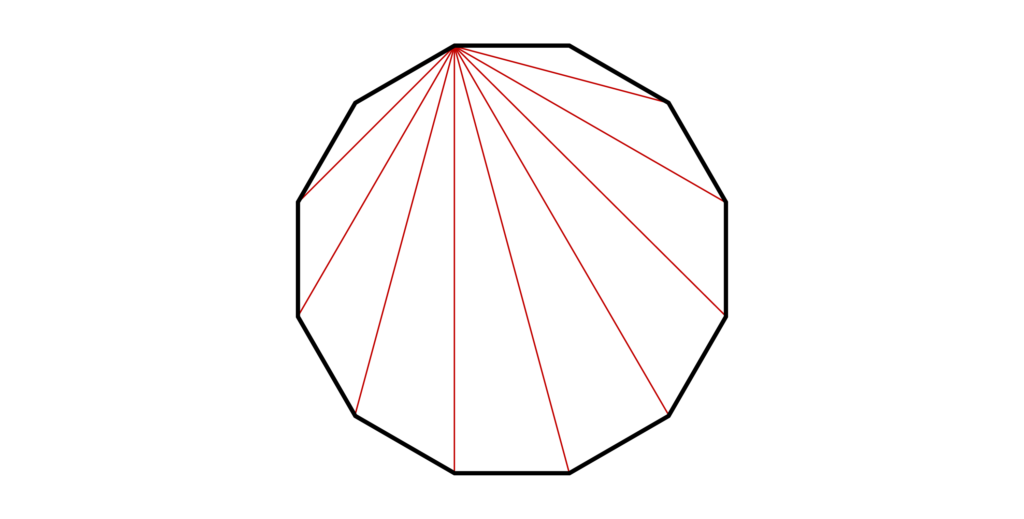
すると、三角形は全部で10個あることがわかります。
ここで、三角形の内角の和=180°でしたね。
よって、十二角形の内角の和は確かに10×180°=1800°となっていることが確認できました。
内角の和が1800°以外のパターン(練習問題)
最後に、内角の和が1800°以外のパターンも求めてみましょう。
内角の和の公式を覚える絶好の機会だと思って解いてみてください。
【練習問題】
(1)内角の和が720°である多角形は何角形か求めよ。
(2)「1つの外角の大きさが72°である正多角形は正n角形である。」nに当てはまる自然数を答えよ。
【解答&解説】
(1)内角の和の公式より、(n-2)×180=720が成り立ちます。
n=6より、六角形・・・(答)となります。
※六角形の内角の和が720度なのはなぜかについて解説した記事もぜひ合わせてご覧ください。
(2)1つの外角の大きさが72°の正多角形ということは、1つの内角の大きさ=180°-72°=108°であることがわかります。
正n角形には内角がn個あるので、内角の和の公式より、(n-2)×180 / n=108が成り立ちます。
両辺にnをかけると、180n-360=108nより、72n=360となります。
したがってn=5・・・(答)となります。
つまり、正五角形の内角の和=108°×5=540°になるというわけですね。
※正五角形の内角の大きさを5秒で求める方法について解説した記事もぜひ合わせてご覧ください。
いかがでしたでしょうか?
今回は内角の和が1800度の多角形を5秒で求める方法について解説しました。
内角の和の公式は図形問題を解くにあたって必須の公式とも言えます。必ず覚えるようにしてください。


